Résonances de Fano à double bande de haute qualité induites par des états liés doubles dans le continuum à l'aide d'une dalle planaire de nanotrous

Introduction

L'amélioration de l'interaction entre la lumière et la matière, qui est importante pour l'amélioration des performances des dispositifs optiques, peut être réalisée en utilisant des réponses de facteur (Q) de haute qualité [1]. La résonance Fano, caractérisée par la forme de ligne asymétrique et le profil spectral net, fournit une approche efficace pour atteindre le facteur Q élevé dans les métamatériaux optiques et a reçu une grande attention [2]. Au cours de la dernière décennie, la résonance de Fano a été signalée dans de nombreux systèmes d'oscillateurs à l'échelle nanométrique activés par des nanostructures plasmoniques [3, 4], où la résonance de Fano est excitée par la résonance du plasma de surface à l'interface métal-diélectrique. Bien que les métamatériaux métalliques soient des candidats prometteurs pour la manipulation de la lumière, la résonance de Fano dans les métamatériaux plasmoniques souffre généralement d'un faible facteur Q dans les régions spectrales du visible au proche infrarouge (NIR) en raison des pertes ohmiques inhérentes au métal.

D'autre part, les métamatériaux entièrement diélectriques fournissent de fortes résonances de type Mie avec des courants de déplacement induits similaires à ceux des métamatériaux plasmoniques, mais présentent moins de pertes dissipatives dans la plage visible à proche infrarouge [5]. L'énergie de la lumière incidente peut être fortement localisée dans les nanostructures diélectriques en raison de l'excitation des résonances dipolaires électriques et/ou magnétiques, ce qui réduit les pertes dissipatives et permet d'obtenir une grande amélioration de la résonance des champs électriques et magnétiques. Ces dernières années, les états liés dans le continuum (BIC) sont devenus le schéma le plus prometteur pour obtenir des réponses à facteur Q élevé dans les métamatériaux entièrement diélectriques [6, 7]. Les BIC résident à l'intérieur du spectre continu des états étendus mais restent contre-intuitivement parfaitement localisés dans l'espace avec une durée de vie théoriquement infinie [8, 9]. Bien que les BIC ne soient pas observables à partir du spectre continu en raison de la propriété non radiative, des résonances Fano à facteur Q élevé peuvent être obtenues lorsque les BIC sont transformés en quasi-BIC (QBIC) [10, 11], les applications potentielles incluent laser [12], filtres optiques [13], conversion de fréquence non linéaire [14], capteurs ultra-sensibles [15, 16] et faisceaux vortex optiques [17].

Généralement, la formation des BIC est fortement liée aux symétries (en plan et en symétrie verticale) de la structure photonique en raison de sa nature interférentielle. Plus particulièrement, les BIC peuvent être perturbés via des nanostructures à incidence oblique ou à symétrie brisée, et les QBIC peuvent être réalisés lorsque le canal de rayonnement entre les états propres et l'espace libre est ouvert [18, 19]. Cependant, la plupart des nanostructures diélectriques utilisées pour exciter les QBIC avec un facteur Q élevé sont compliquées, telles que les nanocroix asymétriques [20], les nanoanneaux asymétriques [21], les nanobarres asymétriques [22,23,24] et les nanotiges asymétriques [25,26, 27,28], qui sont difficiles dans la fabrication en raison de la nécessité d'insérer les fentes profondes sous la longueur d'onde [20,21,22,23,24] ou les nanotrous [25,26,27,28] dans les structures photoniques. D'autres nanostructures telles que les barres rectangulaires remodelées [29, 30] ont des arêtes vives accrues, ce qui les rend plus difficiles à fabriquer avec précision par les techniques lithographiques conventionnelles, ce qui réduit le facteur Q et la durée de vie de résonance des dispositifs en raison de l'ouverture de canaux de fuite supplémentaires [31, 32]. De plus, les nanobarres inclinées [33, 34], un autre type de structures, ont des difficultés à contrôler avec précision l'orientation des nanobars avec les espaces sublongueurs d'onde profonds entre les résonateurs maintenus dans le processus de nanofabrication. Dans les applications, il est utile de réaliser des BIC et des résonances Fano à facteur Q élevé en utilisant des métamatériaux entièrement diélectriques avec des architectures plus simples telles que les dalles planaires nanostructurées [35,36,37,38]. En outre, les résonances multiples de Fano sont très utiles dans les applications telles que l'amélioration de la génération d'harmoniques multibandes [39], la détection multicanal [40] et l'émission de lumière [41]. Par conséquent, il y a un avantage significatif à obtenir des résonances Fano multiples à facteur Q élevé en utilisant une architecture relativement simple basée sur l'excitation des QBIC.

Dans ce travail, une nouvelle dalle planaire de nano-trous (PNS) constituée de trous tétramérisés est proposée pour obtenir des résonances Fano à double bande à facteur Q élevé. En rétrécissant ou en élargissant les trous tétramérisés du PNS le long des diagonales du super-réseau, deux QBIC sont excités et les emplacements des deux résonances de Fano ainsi que leurs facteurs Q peuvent être réglés de manière flexible. Des décompositions multiples en champ lointain et des distributions en champ proche du super-réseau sont effectuées pour révéler les caractéristiques de résonance du PNS, indiquant que les résonances de Fano à double bande résultent des couplages résonnants entre les dipôles toroïdaux électriques ou les dipôles toroïdaux magnétiques. Les résonances Fano à double bande du PNS possèdent une caractéristique indépendante de la polarisation, et elles peuvent survivre même les paramètres géométriques du PNS sont considérablement modifiés, ce qui le rend plus adapté aux applications potentielles.

Méthodes

Structure et conception du treillis

La figure 1 montre la géométrie schématique du PNS proposé et ses spectres de transmission. Le PNS se compose de quatre nanotrous qui peuvent être rétrécis (Δ < 0) ou dilatés (Δ > 0) avec une distance de décalage de le long des diagonales du super-réseau, et Δ = 0 correspond à un réseau simple avec une période réduite de moitié, où chaque nanotrou est situé au centre d'un quart de surface du super-réseau. La période et la hauteur du PNS sont respectivement et H; le rayon du nanotrou est r . L'indice de réfraction du PNS est n _s = 3,2, et le fond est de l'air avec l'indice de réfraction de n _un =  1. La figure 1c montre les spectres du PNS en fonction de la distance de décalage de , où le PNS est éclairé par un x normalement incident -lumière polarisée. Les spectres ainsi que les distributions de champ électromagnétique du PNS présentés dans cet article sont calculés en utilisant le logiciel commercial de la méthode des éléments finis de COMSOL Multiphysics. Comme le montre la figure 1c, il n'y a pas de résonance de Fano pour le PNS non rétréci avec =0. Cependant, deux résonances de Fano avec des profondeurs de modulation de 100 % (définies comme les différences de transmission entre les pics de Fano et les creux de Fano) peuvent être obtenues en rétrécissant ou élargissant légèrement les nanotrous. En comparaison avec la réponse de transmission du PNS non rétréci, la réponse de transmission du PNS rétréci varie brusquement tandis que les bandes latérales sont presque identiques.

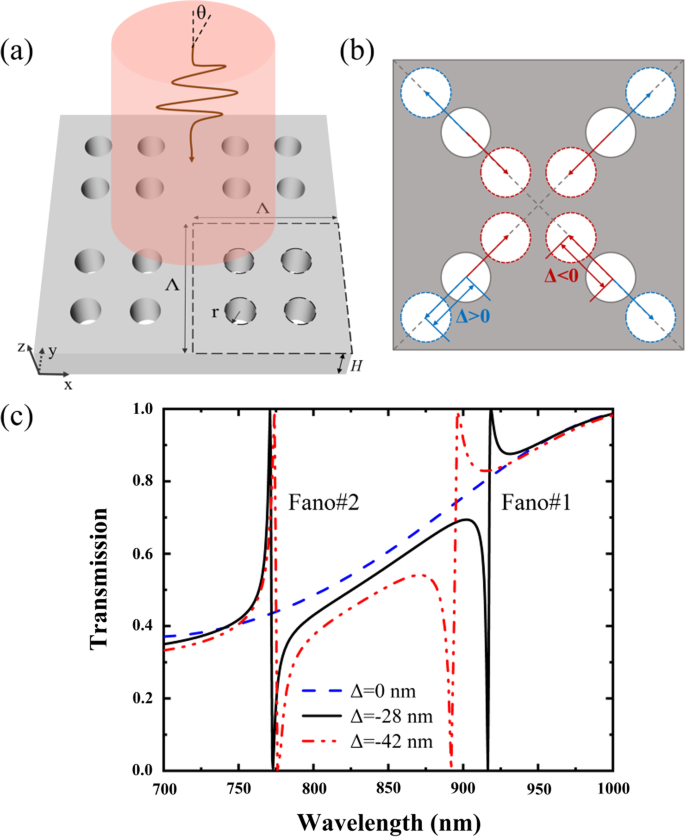
un Vue en perspective du PNS. b Vue verticale du PNS alors que quatre nanotrous rétrécissent (Δ < 0) ou s'étendent (Δ > 0) le long des diagonales du super-réseau. c Spectres de transmission du PNS en fonction de la distance de décalage de . Le PNS est sous l'éclairage du x -onde incidente polarisée avec l'angle incident de θ = 0. Les paramètres du PNS sont :Λ = 350 nm, r = 35 nm et H = 175 nm

Pour montrer clairement l'évolution des résonances de Fano à double bande résultant du rétrécissement ou de l'expansion des trous tétramérisés, la carte de transmission 2D du PNS en fonction de la distance de décalage de est illustrée à la Fig. 2a. Comme le montre la Fig. 2a, deux BIC se produisent dans la région de longueur d'onde d'intérêt comme Δ  =0, et un phénomène similaire de double BIC a déjà été signalé dans les structures des métamembranes à double réseau [13] et du résonateur à anneau fendu [21]. Dans le cas de Δ ≠ 0, des résonances Fano à double bande sont réalisées car les BIC sont induits aux QBIC en raison de la brisure de la symétrie du PNS, c'est-à-dire de la centrosymétrie du réseau simple au quadruple rotation (C_{4 ) symétrie du super-réseau. De plus, parce que le C4 la symétrie du PNS peut être maintenue car les trous tétramérisés sont rétrécis ou agrandis le long des diagonales du super-réseau, les spectres de transmission du PNS sont les mêmes pour la même valeur absolue de |Δ|. En principe, le rétrécissement ou l'expansion des trous tétramérisés réduit la surface de la première zone de Brillouin du PNS à mesure que la cellule unitaire du PNS passe du simple réseau au super-réseau, et le BIC protégé par la symétrie peut être excité à incidence normale en raison de la introduction d'une perturbation de surface ainsi que d'un plissement de la zone de Brillouin du PNS [42, 43]. Généralement, le facteur Q d'un BIC protégé contre la symétrie montre une dépendance carrée inverse du degré d'asymétrie δ basé sur la théorie des perturbations [21] :}

où ĸ est une constante de proportionnalité, S est l'aire d'un super-réseau, ω est la fréquence angulaire et le paramètre d'asymétrie est \(\delta { =}\sqrt 2 \Delta /\Lambda\).

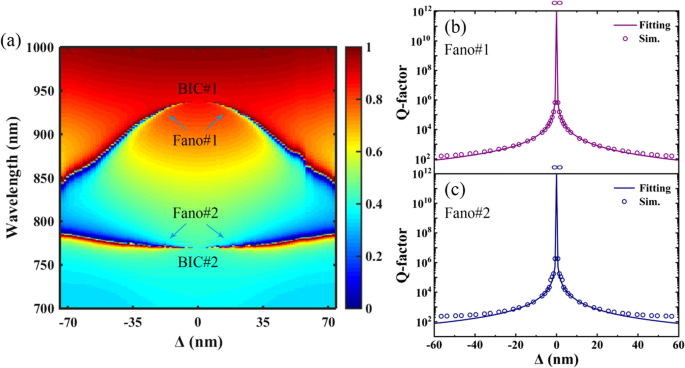
un Carte 2D de transmission du PNS en fonction de la distance de décalage de le long des diagonales du super-réseau. b et c Le facteur Q et le résultat d'ajustement de Fano#1 et Fano#2, respectivement. Les autres paramètres sont les mêmes que sur la figure 1c

La figure 2b, c montre le facteur Q et le résultat d'ajustement de Fano#1 et Fano#2, respectivement. Le facteur Q du PNS est calculé comme un rapport entre la longueur d'onde de résonance λ _r et sa pleine largeur à mi-hauteur (FWHM) , où est la région de longueur d'onde entre le pic et le creux de la résonance de Fano. Les résultats d'ajustement du PNS sont calculés en utilisant l'Eq. (1). Comme le montre la Fig. 2b, c, les trajectoires divergentes du PNS où les facteurs Q divergent à l'infini à Δ  =0 sont validées en utilisant la relation carrée inverse pour ajuster les données. D'excellents résultats d'ajustement peuvent être obtenus et le léger désaccord à une plus grande asymétrie est dû à l'écart par rapport à l'hypothèse d'une petite perturbation dans l'équation. (1). L'avantage significatif du PNS est que l'emplacement et le facteur Q des résonances Fano double bande peuvent être adaptés en réduisant ou en élargissant les trous tétramérisés, ce qui facilite le contrôle dynamique des performances de résonance du multiple à facteur Q élevé. Résonances Fano.

Mécanismes physiques et interprétation

Pour avoir un aperçu de l'origine des résonances Fano à double bande via la réduction ou l'expansion des trous tétramérisés du PNS, nous décomposons le rayonnement en champ lointain de la résonance BIC et Fano en contributions de différents composants multipolaires pour discuter plus en détail de leurs caractéristiques. Les moments multipolaires peuvent être calculés sur la base de la densité de courant de déplacement j dans le super-réseau du PNS [26, 44, 45] :

où P , M , T , Q ^{(e )} et Q ^{(m )} sont les moments du dipôle électrique (ED), du dipôle magnétique (MD), du dipôle toroïdal (TD), du quadripôle électrique (EQ) et du quadripôle magnétique (MQ), respectivement ; c est la vitesse de la lumière dans le vide, et α , β = x , y , z . Ici la densité de charge ρ , qui apparaît généralement dans la définition de ED et MQ, a été remplacé par la densité de courant de déplacement j via la relation de conservation de charge de \(i\omega \rho + \nabla \cdot {\varvec{j}} =0\). En cas d'excitation harmonique ~ exp(iωt ), le pouvoir de diffusion des moments multipolaires induits contribuant à la réponse en champ lointain peut s'écrire sous la forme :

où les deux premiers termes correspondent à la diffusion conventionnelle ED (charge) et MD. Le troisième terme correspond à la diffusion TD. Les quatrième et cinquième termes proviennent de EQ et MQ. Le dernier terme est le terme d'ordre supérieur qui contient la diffusion multipolaire d'ordre élevé et le couplage entre eux et peut être généralement ignoré. En utilisant les équations. (2)–(7), les contributions de différents multipôles à la puissance de diffusion du champ lointain peuvent être obtenues.

La figure 3 montre la puissance de diffusion de différents multipôles du PNS pour différentes distances de décalage de , les autres paramètres sont les mêmes que sur la figure 1c. Comme le montre la Fig. 3a–d, pour le PNS avec Δ = 0, ED et MD sont les dipôles dominants et ils ne résonnent pas dans la région de longueur d'onde d'intérêt. Cependant, en réduisant ou en agrandissant les nanotrous du PNS avec |Δ|≠ 0, des résonances Fano à double bande peuvent être réalisées en raison des excitations des modes dipolaires résonnants. Pour voir clairement les rôles importants des modes dipolaires résonnants dans la formation des résonances de Fano à double bande observées, la figure 3e, f montre la puissance de diffusion normalisée de différents multipôles avec Δ =  − 28 nm autour de Fano#1 et Fano#2, respectivement . Comme le montre la figure 3e, les modes de résonance dominants sont ED et TD autour de Fano#1, et Fano#1 est la conséquence directe du couplage résonant des dipôles électriques toroïdaux. En particulier, ED et TD sont fortement améliorés à une amplitude comparable à la pointe de résonance (918,5 nm) de Fano 1 ; ainsi, une transmission à 100% peut être obtenue en raison de l'interférence destructive entre ED et TD. Alors que pour le creux de résonance (916,5 nm) de Fano#1, la réflexion est maximisée et la transmission passe à zéro en raison de la diffusion améliorée de ED et TD. De même, comme le montre la Fig. 3f, Fano # 2 résulte du couplage résonant des dipôles magnétiques toroïdaux, sa pointe (771,1 nm) indique l'interférence destructive entre MD et TD, tandis que son pendage (772,9 nm) est associé à la diffusion améliorée de MD et TD. Notez qu'en raison du fort couplage des dipôles toroïdaux électriques ou des dipôles toroïdaux magnétiques, les modes de résonance sont robustes à la fois pour Fano#1 et Fano#2 même si Δ est varié.

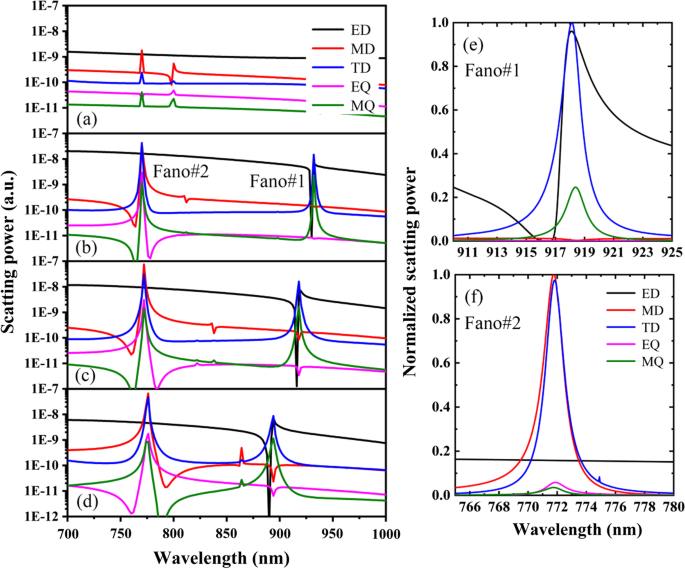
Pouvoir de diffusion des cartésiens ED, MD, TD, EQ et MQ lorsque a Δ = 0, b Δ =  − 14 nm, c Δ =  − 28 nm et d =  − 42 nm. e et f Pouvoir de diffusion normalisé de différents multipôles avec Δ =  − 28 nm autour de Fano#1 et Fano#2, respectivement. Les autres paramètres sont les mêmes que sur la figure 1c

Pour lier la réponse de transmission des résonances de Fano à double bande dans le champ lointain avec les excitations des moments multipolaires induits, les distributions du champ électromagnétique et du courant de déplacement des résonances de Fano du super-réseau du PNS sont illustrées à la Fig. 4. Fig. 4a, b, le champ électrique de Fano#1 est bien confiné dans le super-réseau du PNS avec le courant de déplacement le long du x axe, indiquant un mode de résonance ED. De plus, le courant de déplacement de Fano#1 forme deux boucles inversées entre le centre et les bords du super-réseau, et le champ magnétique forme une boucle dans le yz plan, correspondant à un mode de résonance TD le long du x axe [44, 46]. Par conséquent, Fano#1 est issu du couplage résonant entre les modes ED et TD, qui sont en ligne avec les résultats prédits des décompositions multipolaires comme mentionné ci-dessus. En fait, en raison des caractéristiques de résonance des dipôles toroïdaux électriques de Fano # 1, les distributions du champ électromagnétique et du courant de déplacement au pic de résonance (918,5 nm), à la longueur d'onde centrale (917,5 nm) et au creux de résonance (916,5 nm) de Fano #1 sont presque les mêmes, à l'exception d'une légère différence dans l'amplitude du champ (Fichier supplémentaire 1 :Fig. S1). Dans le cas de Fano # 2, comme le montre la figure 4c, le champ électrique est fortement amélioré et le courant de déplacement forme deux boucles inversées entre le centre du super-réseau et le super-réseau voisin du PNS, indiquant un mode de résonance TD le long de la z axe. De plus, le champ magnétique de Fano#2 est très localisé dans le super-réseau avec la direction le long du y axe, comme le montre la Fig. 4d, avec un mode de résonance MD. En conséquence, Fano#2 est la conséquence directe du couplage résonant des dipôles magnétiques toroïdaux, ce qui est en accord avec la prédiction des décompositions multipolaires du champ lointain du PNS. De plus, en raison du couplage des dipôles magnétiques toroïdaux de Fano n°2, le champ électromagnétique et le courant de déplacement au pic de résonance (771,1 nm), la longueur d'onde centrale (772,0 nm) et le pendage de résonance (722,9 nm) de Fano n°2 sont similaires distributions (Fichier supplémentaire 1 :Figure S2).

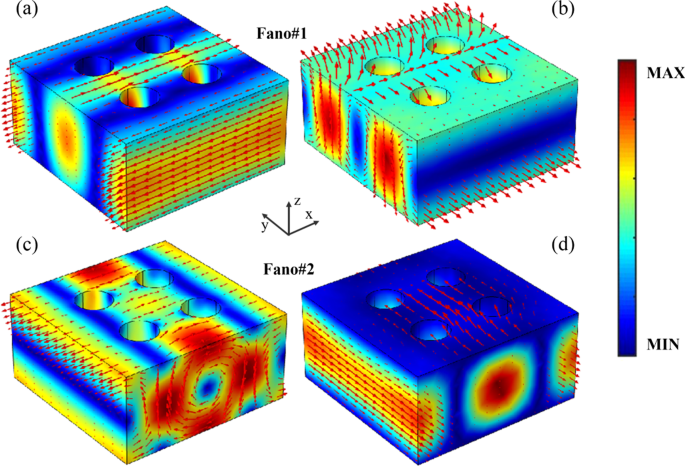
Distributions du champ électromagnétique et du courant de déplacement des résonances de Fano du super-réseau du PNS, la barre de couleur représente l'amplitude du champ et les flèches rouges indiquent le vecteur de champ ou le vecteur de courant de déplacement. Les autres paramètres sont les mêmes que sur la Fig. 1c avec Δ =  − 28 nm. un et c Distributions d'amplitude de champ électrique et vecteur de courant de déplacement de Fano#1 et Fano#2, respectivement. b et d Distributions de l'amplitude du champ magnétique et du vecteur de champ magnétique de Fano#1 et Fano#2, respectivement

Résultats et discussion

La figure 5 montre les spectres de transmission du PNS en fonction du rayon r du nanotrou, et les autres paramètres sont les mêmes que sur la figure 1c avec Δ =  − 28 nm. Comme le montre la Fig. 5a, les résonances Fano double bande peuvent être maintenues comme r varie de 0 à la valeur maximale de 67,5 nm, c'est-à-dire , les trous tétramérisés sont tangents les uns aux autres dans le super-réseau. L'augmentation du rayon du nanotrou r augmente les perturbations de surface du PNS et réduit également son indice de réfraction effectif (ERI), ce qui entraîne l'augmentation du facteur Q et le décalage vers le bleu des résonances de Fano. Plus précisément, l'emplacement de résonance de Fano#1 est plus sensible à la variation de r , et les résonances de Fano à double bande ont tendance à fusionner en un seul mode de résonance lorsque les trous tétramérisés se rapprochent les uns des autres. Comme le montre la figure 5b, l'augmentation de r non seulement blueshifts l'emplacement de résonance des résonances de Fano, mais augmente également leurs FWHM. En tant que r est augmenté de 25 à 45 nm, les pics de résonance de Fano#1 et Fano#2 sont décalés vers le bleu de 936,7 nm et 793,2 nm à 887,6 nm et 743,8 nm, respectivement ; et leurs FWHM sont augmentées de 0,8 nm et 0,6 nm à 6,8 nm et 3,1 nm, respectivement. Notez l'augmentation de r améliore également les profondeurs de modulation des résonances Fano, et des profondeurs de modulation de 100 % peuvent être réalisées en tant que r est supérieure à 30 nm. De plus, en évaluant le décalage de la longueur d'onde du pic de Fano affecté par les paramètres structurels du PNS, il est montré que le rayon du nanotrou r est les paramètres structurels les plus sensibles pour Fano#1 et Fano#2 (Fichier supplémentaire 1 :Figure S3). Par conséquent, la variation de r fournit une approche efficace pour contrôler dynamiquement les performances de résonance des résonances Fano double bande du PNS.

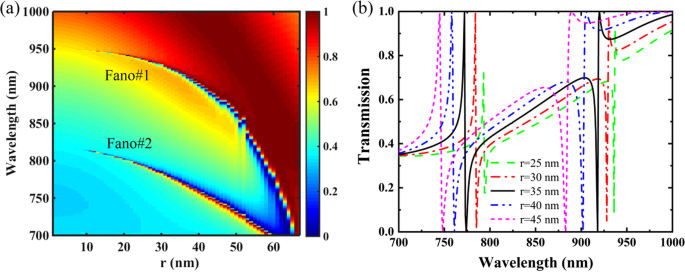
un Carte de transmission 2D du PNS en fonction du rayon r du nanotrou. b Spectres de transmission du PNS pour différents rayons de nanotrous r . Les autres paramètres sont les mêmes que sur la Fig. 1c avec Δ =  − 28 nm

La figure 6 montre les influences de la symétrie de la structure sur les réponses de transmission du PNS, où le rayon r' de deux nanotrous varie de zéro à tangent l'un à l'autre, et les autres paramètres sont les mêmes que sur la figure 1c avec Δ =  − 28 nm. Comme le montre la figure 6a, pour le super-réseau avec symétrie miroir le long du x axe (direction du champ électrique de la lumière incidente), comme le rayon r ′ des deux nanotrous est augmenté, les emplacements de résonance des résonances Fano à double bande sont décalés vers le bleu en raison de la diminution de l'ERI du PNS, et leurs bandes passantes sont élargies en raison des perturbations de surface accrues. Cependant, comme le montre la figure 6b, bien que les deux résonances de Fano puissent être maintenues avec l'augmentation de r ′, deux résonances Fano supplémentaires se produiront en tant que symétrie miroir du super-réseau le long du x l'axe est cassé. En général, briser la symétrie structurelle le long du x (y ) brisera également la symétrie du mode le long de l'axe x (y ) d'un réseau périodique, et le mode non radiatif non dégénéré est capable de se coupler au rayonnement extérieur grâce à sa composante dégénérée [47]. Par conséquent, le fait que les deux résonances de Fano supplémentaires soient présentes uniquement pour la structure à symétrie brisée le long de x l'axe indique qu'elles sont dues aux modes non dégénérés perturbés.

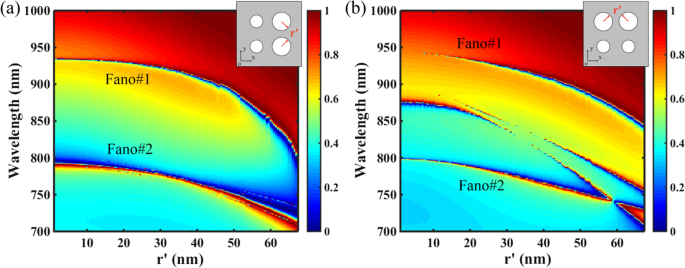
Influences de la symétrie de la structure sur les réponses de transmission du SNP. Les autres paramètres sont les mêmes que sur la Fig. 1c avec Δ =  − 28 nm. Les figures d'insertion indiquent le schéma de principe du super-réseau du PNS. un Carte de transmission 2D du PNS en fonction du rayon r ′ de deux nanotrous, où la symétrie structurelle du super-réseau le long du x l'axe est maintenu. b Carte de transmission 2D du PNS en fonction du rayon r ′ de deux nanotrous, où la symétrie structurelle du super-réseau le long du x l'axe est cassé

Nous avons en outre caractérisé les performances de résonance du PNS sous les influences de l'angle d'incidence et de l'angle de polarisation. Comme le montre la figure 7a, les résonances Fano à double bande du PNS sont immunisées contre la variation de l'angle de polarisation due au C₄ topologie symétrique. Comme l'angle de polarisation est modifié de 0 à 90°, c'est-à-dire de x -polarisation à y -polarisation, Fano#1 et Fano#2 restent les mêmes. Cependant, dans le cas de l'angle incident, comme le montre la Fig. 7b, bien que Fano#1 soit également insensible à la variation de l'angle incident, Fano#2 est décalé vers le rouge lorsque l'angle incident s'écarte de l'incidence normale, et une résonance Fano supplémentaire (Fano#3) se produit en raison de la suppression de la décroissance du rayonnement du BIC protégé par la symétrie est annulée à une incidence anormale. En général, ce type de suppression de la décroissance du rayonnement du BIC est étroitement lié à l'interférence destructive entre les champs de rayonnement émis par deux modes de fuite contra-propagatifs à l'un ou l'autre des deux bords de la bande d'arrêt des réseaux périodiques [48]. Notez qu'en raison du fort couplage entre Fano#2 et Fano#3, une fenêtre de transparence induite étroite peut être excitée dans la région voisine entre eux.

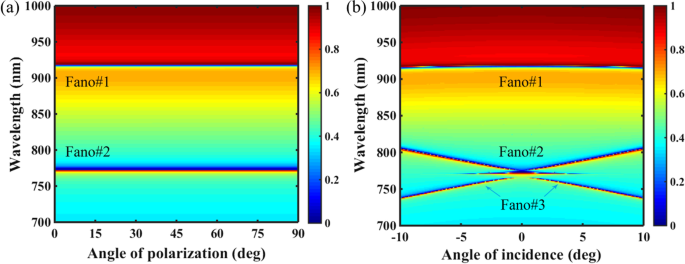
un Carte 2D de transmission du PNS en fonction de l'angle de polarisation. b Carte 2D de transmission du PNS en fonction de l'angle d'incidence. Les autres paramètres sont les mêmes que sur la Fig. 1c avec Δ =  − 28 nm

Enfin, nous avons montré que plusieurs résonances de Fano peuvent être obtenues en augmentant la hauteur de dalle H du PNS. La figure 8 montre la carte de transmission 2D du PNS en fonction de H pour les structures non rétrécies (Δ = 0 nm) et rétrécies (Δ =  − 28 nm). Comme le montre la figure 8a, il n'y a pas de résonance de Fano, à l'exception des résonances de Fabry-Pérot (F-P) pour le PNS non rétréci lorsque H varie. Selon la théorie F-P, la condition de résonance de la cavité F-P du PNS non rétréci peut être écrite comme :

où δ est le déphasage, λ est la longueur d'onde dans l'espace libre, n _eff est l'ERI de la dalle homogène équivalente du PNS, φ est la phase supplémentaire et m est un entier qui indique l'ordre de résonance. En utilisant la théorie du milieu effectif [49], l'ERI du PNS peut être estimé comme :

où f est le facteur de remplissage du PNS, et f = 1 − 4π(r /Λ) ² .

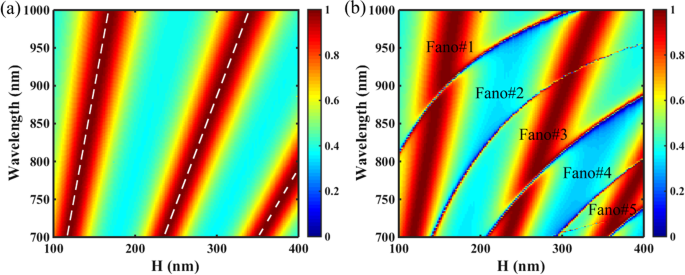
un Carte de transmission 2D du PNS en fonction de la hauteur de dalle H avec Δ = 0 nm, les lignes pointillées blanches sont les résultats du modèle de cavité F–P. b Carte 2D de transmission du PNS en fonction de la hauteur de dalle H avec Δ =  − 28 nm. Les autres paramètres sont les mêmes que sur la figure 1c

En utilisant les équations. (8) et (9), les emplacements de la résonance F–P du PNS non rétréci peuvent être calculés comme λ _F–P = 2π ·H·n _eff /(mπ -φ ). En calcul, bien que la phase supplémentaire φ ne peut pas être traité comme une constante car il affecte évidemment le déphasage δ , ses valeurs peuvent être déterminées en utilisant la méthode d'ajustement linéaire [50, 51]. La figure 8a montre la carte de transmission 2D du PNS avec Δ = 0 nm, et les résultats de la théorie F–P sont indiqués par les lignes en pointillés blancs. Comme le montre la figure 8a, les lignes pointillées blanches du modèle de cavité F-P coïncident avec celles des pics de transmission du PNS, confirmant que c'est la résonance F-P qui améliore la transmission du PNS non rétréci dans le région spectrale d'intérêt. Cependant, comme le montre la figure 8b, pour le PNS rétréci avec Δ =  − 24 nm, cinq résonances Fano avec un facteur Q élevé sont excitées et coexistent avec les résonances F-P lorsque H varie dans la plage de 100 à 400 nm , les résonances Fano sont si fortes qu'elles divisent les résonances F–P dans la région de croisement entre les résonances Fano et F–P. Selon la théorie du guide d'onde en plaque, l'augmentation de l'épaisseur de la plaque de cristal photonique assure des modes de fuite plus limités dans la structure [32, 52] ; ainsi, le nombre de résonances de Fano peut être augmenté en augmentant simplement l'épaisseur du PNS. Notez que le décalage des trous tétramérisés ne changera pas l'ERI du PNS, donc les emplacements des résonances F-P sont conservés presque les mêmes pour les structures non rétrécies et rétrécies.

Conclusions

Des résonances Fano double bande à facteur Q élevé peuvent être réalisées en utilisant une architecture de PNS relativement simple basée sur l'excitation de QBIC doubles. By shrinking or expanding four nanoholes of the PNS along the diagonals of the superlattice, two symmetry-protected BICs can be transformed to dual-band Fano resonances and their locations as well as their Q-factors can be flexibly tuned. The dual-band Fano resonances of the PNS are resulted from the resonant couplings between the electric toroidal dipoles or the magnetic toroidal dipoles, and their correlations between the far-field multiple decompositions and the near-field distributions of the superlattice are verified. The dual-band Fano resonances of the PNS possess polarization-independent feature, and their high-Q-factor features are robust to the variations of the geometric parameters. By increasing the height of the PNS, the number of high-Q-factor Fano resonances can be improved as more leaky modes can be supported by the structure. Our results give more tuning freedoms for the realization of high-Q-factor resonators with better performances, which may provide a further step in the development of lasing, sensing and nonlinear photonics.

Disponibilité des données et des matériaux

Les ensembles de données utilisés et/ou analysés au cours de la présente étude sont disponibles auprès de l'auteur correspondant sur demande raisonnable.

Abréviations

Q-factor:

Quality factor

PNS:

Planar nanohole slab

BICs:

Bound states in the continuum

NIR:

Near-infrared

QBICs:

Quasi-BICs

FWHM:

Full width at half maximum

DE :

Dipôle électrique

MD :

Dipôle magnétique

TD:

Toroidal dipole

EQ :

Quadrupôle électrique

MQ :

Quadrupôle magnétique

ERI:

Effective refractive index

F–P:

Fabry–Pérot