Notation sous forme polaire et sous forme rectangulaire pour les nombres complexes

Afin de travailler avec des nombres complexes sans dessiner de vecteurs, nous avons d'abord besoin d'une sorte de notation mathématique standard. Il existe deux formes de base de notation des nombres complexes :polaire et rectangulaire .

Forme polaire d'un nombre complexe

La forme polaire est l'endroit où un nombre complexe est désigné par la longueur (autrement connu sous le nom de grandeur , valeur absolue , ou module ) et l'angle de son vecteur (généralement désigné par un symbole d'angle qui ressemble à ceci : ).

Pour utiliser l'analogie de la carte, la notation polaire pour le vecteur de New York à San Diego serait quelque chose comme "2400 miles, sud-ouest". Voici deux exemples de vecteurs et leurs notations polaires :

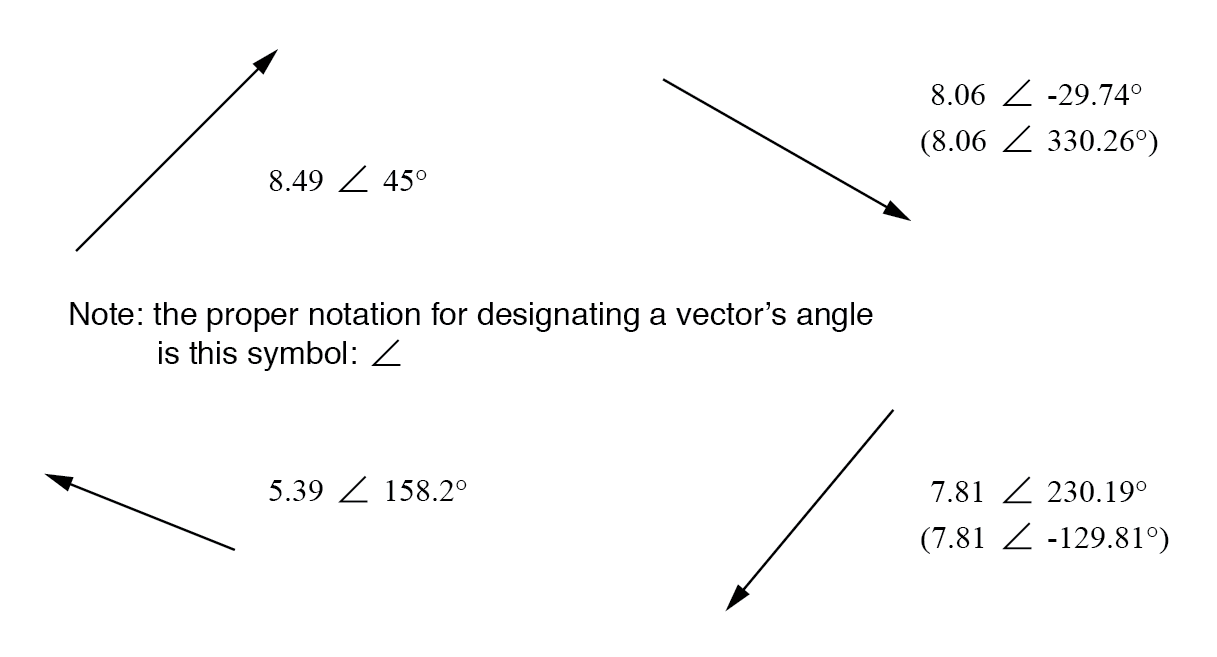
Vecteurs avec notations polaires.

L'orientation standard pour les angles vectoriels dans les calculs de circuits CA définit 0° comme étant vers la droite (horizontal), faisant 90° vers le haut, 180° vers la gauche et 270° vers le bas. Veuillez noter que les vecteurs inclinés vers le bas peuvent avoir des angles représentés sous forme polaire sous forme de nombres positifs supérieurs à 180 ou de nombres négatifs inférieurs à 180.

Par exemple, un vecteur angulaire 270° (droit vers le bas) peut également être considéré comme ayant un angle de -90°. (Figure ci-dessous) Le vecteur ci-dessus à droite (7,81 ∠ 230,19°) peut également être noté 7,81 ∠ -129,81°.

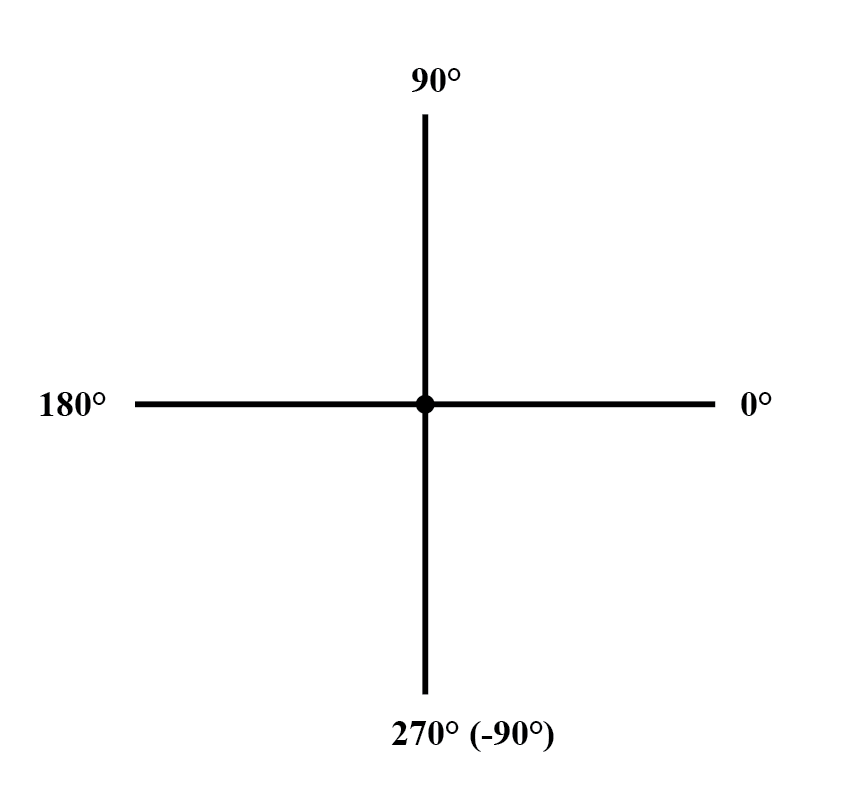
La boussole vectorielle.

Forme rectangulaire d'un nombre complexe

La forme rectangulaire, d'autre part, est l'endroit où un nombre complexe est désigné par ses composants horizontaux et verticaux respectifs. Essentiellement, le vecteur angulaire est considéré comme l'hypoténuse d'un triangle rectangle, décrit par les longueurs des côtés adjacents et opposés.

Plutôt que de décrire la longueur et la direction d'un vecteur en indiquant la magnitude et l'angle, il est décrit en termes de « à quelle distance gauche/droite » et « à quelle distance haut/bas ».

Ces figures bidimensionnelles (horizontales et verticales) sont symbolisées par deux figures numériques. Afin de distinguer les dimensions horizontales et verticales l'une de l'autre, la verticale est précédée d'un « i » minuscule (en mathématiques pures) ou d'un « j » (en électronique).

Ces lettres minuscules ne représentent pas une variable physique (telle que le courant instantané, également symbolisé par une lettre minuscule "i"), mais sont plutôt des opérateurs mathématiques utilisé pour distinguer la composante verticale du vecteur de sa composante horizontale. En tant que nombre complexe complet, les quantités horizontales et verticales sont écrites sous forme de somme :(Figure ci-dessous)

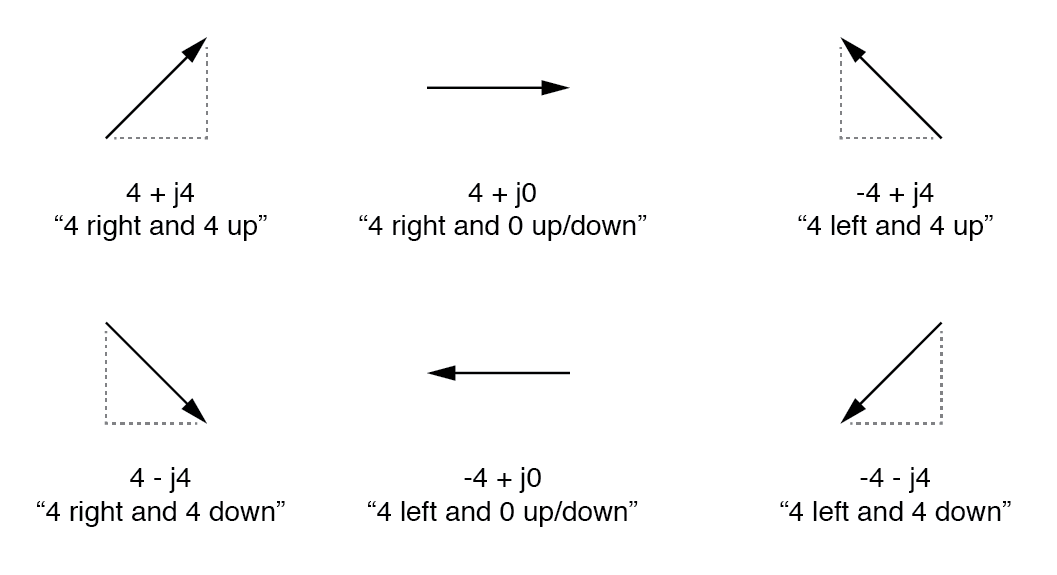
Dans la forme "rectangulaire", la longueur et la direction du vecteur sont indiquées en termes de portée horizontale et verticale, le premier nombre représentant l'horizontale ("réel") et le second nombre (avec le préfixe « j ») représentant les dimensions verticales (« imaginaires »).

La composante horizontale est appelée le réel car cette dimension est compatible avec les nombres scalaires (« réels ») normaux. La composante verticale est appelée l'imaginaire composante puisque cette dimension se situe dans une direction différente, totalement étrangère à l'échelle des nombres réels. (Figure ci-dessous)

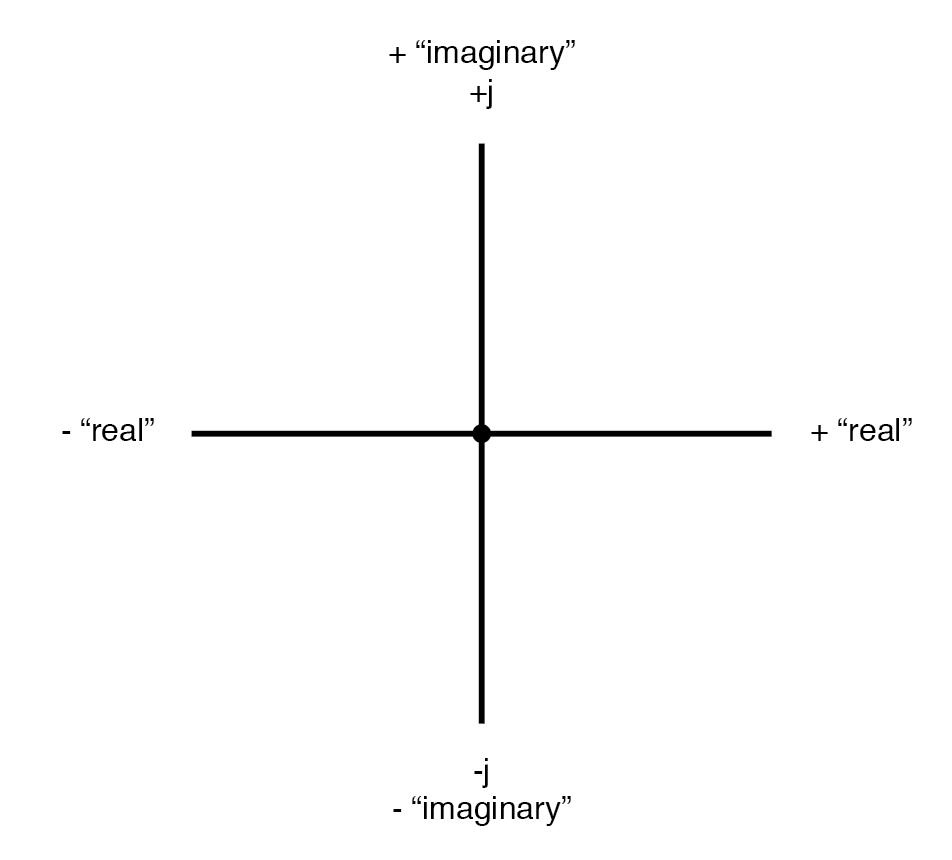
Boussole vectorielle montrant les axes réels et imaginaires.

L'axe « réel » du graphique correspond à la droite numérique familière que nous avons vue plus tôt :celle qui contient à la fois des valeurs positives et négatives. L'axe « imaginaire » du graphique correspond à une autre droite numérique située à 90° de la « vraie ».

Les vecteurs étant des choses à deux dimensions, nous devons avoir une « carte » à deux dimensions sur laquelle les exprimer, donc les deux droites numériques perpendiculaires l'une à l'autre :(Figure ci-dessous)

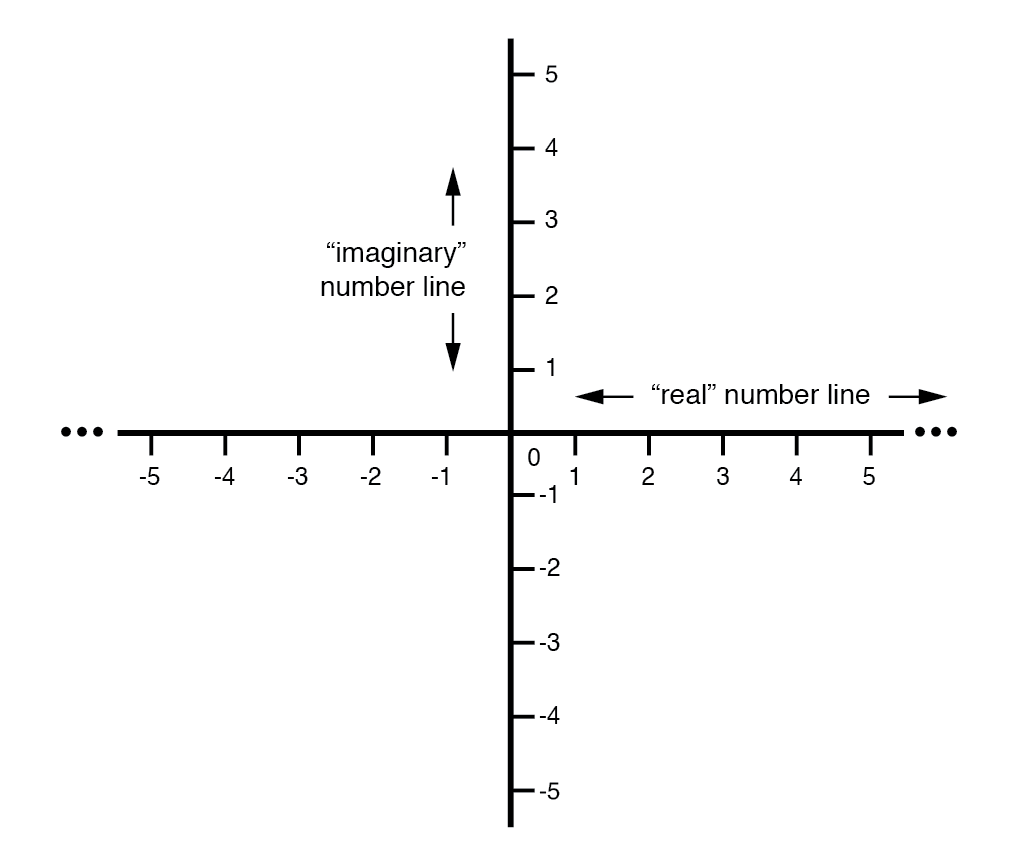
Boussole vectorielle avec droites numériques réelles et imaginaires ("j").

Conversion de la forme polaire en forme rectangulaire

L'une ou l'autre méthode de notation est valable pour les nombres complexes. La principale raison d'avoir deux méthodes de notation est la facilité de calcul à la main, la forme rectangulaire se prêtant à l'addition et la soustraction, et la forme polaire se prêtant à la multiplication et à la division.

La conversion entre les deux formes de notation implique une trigonométrie simple. Pour convertir du polaire au rectangulaire, trouvez la composante réelle en multipliant la magnitude polaire par le cosinus de l'angle, et la composante imaginaire en multipliant la magnitude polaire par le sinus de l'angle.

Cela peut être compris plus facilement en traçant les quantités comme les côtés d'un triangle rectangle, l'hypoténuse du triangle représentant le vecteur lui-même (sa longueur et son angle par rapport à l'horizontale constituant la forme polaire), les côtés horizontaux et verticaux représentant le " composants rectangulaires réels" et "imaginaires", respectivement :(Figure ci-dessous)

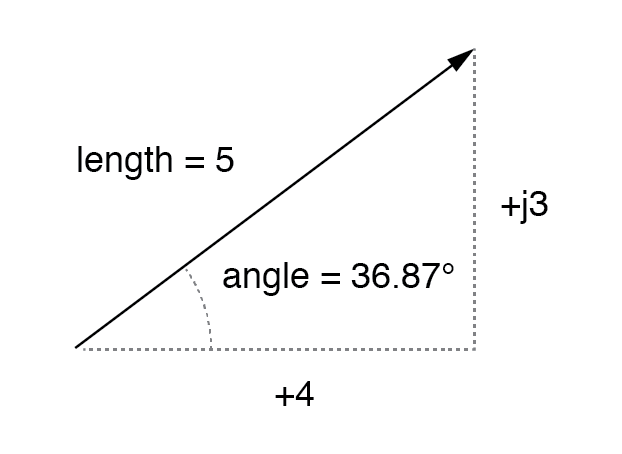
Vecteur de magnitude en termes de composants réels (4) et imaginaires (j3).

Conversion de la forme rectangulaire en forme polaire

Pour convertir de rectangulaire à polaire, trouvez la magnitude polaire à l'aide du théorème de Pythagore (la magnitude polaire est l'hypoténuse d'un triangle rectangle et les composantes réelle et imaginaire sont respectivement les côtés adjacent et opposé) et l'angle par en prenant l'arc tangente de la composante imaginaire divisée par la composante réelle :

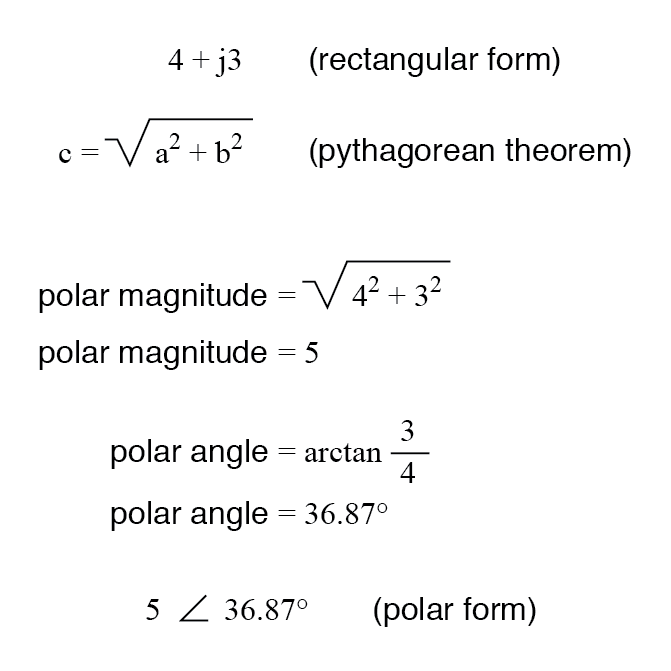
AVIS :

• Polaire la notation désigne un nombre complexe en termes de longueur de son vecteur et de direction angulaire à partir du point de départ. Exemple :voler 45 miles ∠ 203 ° (ouest par sud-ouest).
• Rectangulaire la notation désigne un nombre complexe par ses dimensions horizontale et verticale. Exemple :conduisez 41 miles vers l'ouest, puis tournez et conduisez 18 miles vers le sud.
• En notation rectangulaire, la première quantité est la composante « réelle » (dimension horizontale du vecteur) et la deuxième quantité est la composante « imaginaire » (dimension verticale du vecteur). Le composant imaginaire est précédé d'un « j » minuscule, parfois appelé l'opérateur j .
• Les formes polaires et rectangulaires de notation pour un nombre complexe peuvent être liées graphiquement sous la forme d'un triangle rectangle, l'hypoténuse représentant le vecteur lui-même (forme polaire :longueur de l'hypoténuse =magnitude ; angle par rapport au côté horizontal =angle ), le côté horizontal représentant le composant rectangulaire "réel" et le côté vertical représentant le composant rectangulaire "imaginaire".

FEUILLE DE TRAVAIL CONNEXE :

• Fiche de travail de la phase AC