Loi de tension de Kirchhoff (KVL)

Qu'est-ce que la loi de tension de Kirchhoff (KVL) ?

Le principe connu sous le nom de Loi de tension de Kirchhoff (découvert en 1847 par Gustav R. Kirchhoff, un physicien allemand) peut s'énoncer ainsi :

« La somme algébrique de toutes les tensions dans une boucle doit être égale à zéro »

Par algébrique , je veux dire tenir compte des signes (polarités) ainsi que des grandeurs. Par boucle , je veux dire tout chemin tracé d'un point d'un circuit à d'autres points de ce circuit, et enfin de retour au point initial.

Démonstration de la loi de tension de Kirchhoff dans un circuit en série

Jetons un autre coup d'œil à notre exemple de circuit en série, en numérotant cette fois les points du circuit pour la référence de tension :

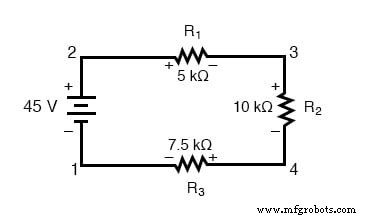
Si nous devions connecter un voltmètre entre les points 2 et 1, le câble de test rouge au point 2 et le câble de test noir au point 1, le compteur enregistrerait +45 volts. En règle générale, le signe « + » n'est pas affiché mais plutôt implicite, pour les lectures positives sur les affichages des compteurs numériques. Cependant, pour cette leçon, la polarité de la lecture de tension est très importante et je vais donc montrer explicitement les nombres positifs :

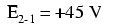
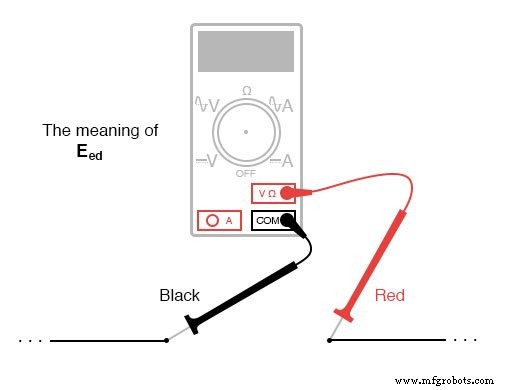
Lorsqu'une tension est spécifiée avec un double indice (les caractères "2-1" dans la notation "E_2-1 "), cela signifie la tension au premier point (2) telle que mesurée par rapport au deuxième point (1). Une tension spécifiée comme « E_cd " signifierait la tension indiquée par un compteur numérique avec le fil de test rouge au point "c" et le fil de test noir au point "d":la tension à "c" en référence à "d".

Si nous devions prendre ce même voltmètre et mesurer la chute de tension à travers chaque résistance, en parcourant le circuit dans le sens des aiguilles d'une montre avec le fil de test rouge de notre compteur sur le point devant et le fil de test noir sur le point derrière, nous obtiendrions les lectures suivantes :

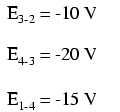
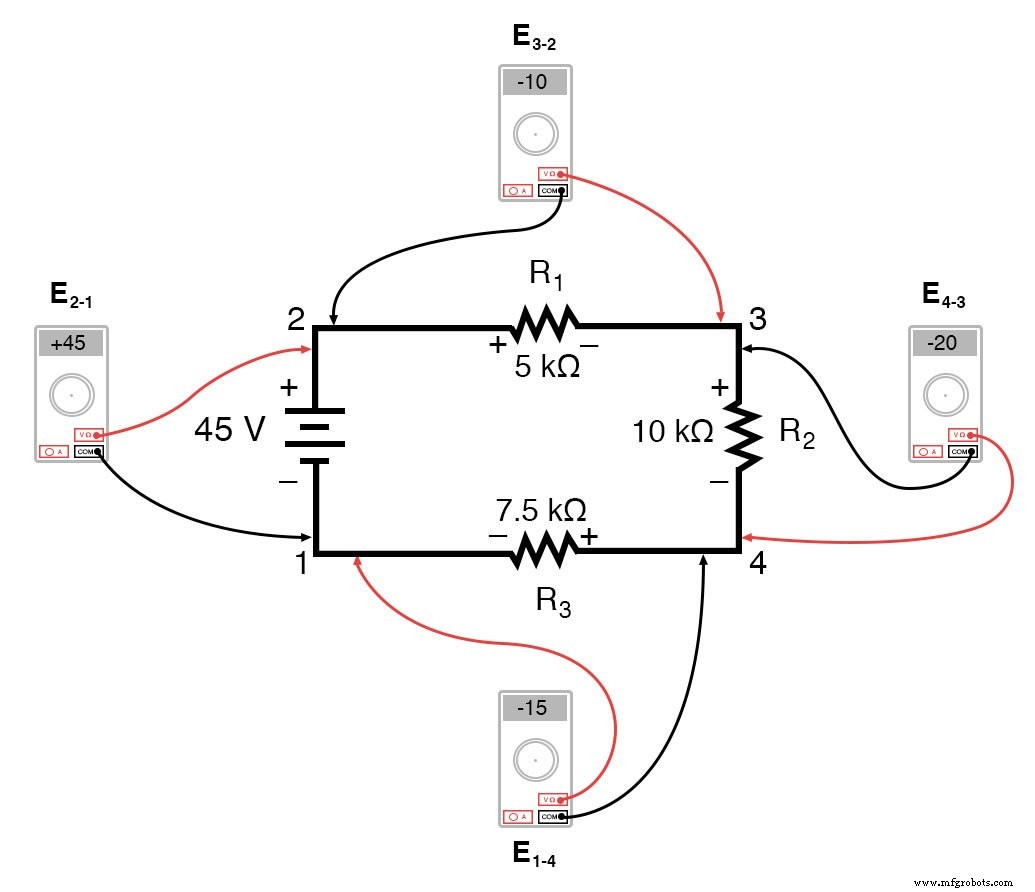
Nous devrions déjà être familiarisés avec le principe général des circuits en série indiquant que les chutes de tension individuelles s'ajoutent à la tension totale appliquée, mais mesurer les chutes de tension de cette manière et faire attention à la polarité (signe mathématique) des lectures révèle une autre facette de cela. principe :que les tensions mesurées comme telles s'additionnent toutes à zéro :

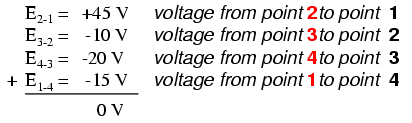
Dans l'exemple ci-dessus, la boucle a été formée par les points suivants dans cet ordre :1-2-3-4-1. Peu importe à quel point nous commençons ou dans quelle direction nous procédons en traçant la boucle; la somme de tension sera toujours égale à zéro. Pour le démontrer, on peut additionner les tensions dans la boucle 3-2-1-4-3 du même circuit :

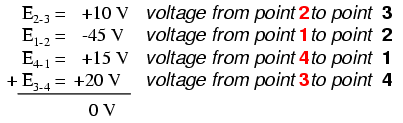
Cela peut avoir plus de sens si nous redessinons notre exemple de circuit en série afin que tous les composants soient représentés en ligne droite :

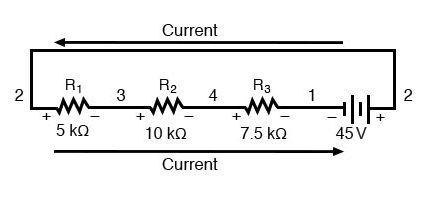
C'est toujours le même circuit en série, juste avec les composants disposés sous une forme différente. Remarquez les polarités des chutes de tension de la résistance par rapport à la batterie :la tension de la batterie est négative à gauche et positive à droite, alors que toutes les chutes de tension de la résistance sont orientées dans l'autre sens :positive à gauche et négative à droite. C'est parce que les résistances résistent le flux de charge électrique étant poussé par la batterie. Autrement dit, la « poussée » exercée par les résistances contre le flux de charge électrique doit être dans une direction opposée à la source de la force électromotrice.

Ici, nous voyons ce qu'un voltmètre numérique indiquerait sur chaque composant de ce circuit, le fil noir à gauche et le fil rouge à droite, comme présenté de manière horizontale :

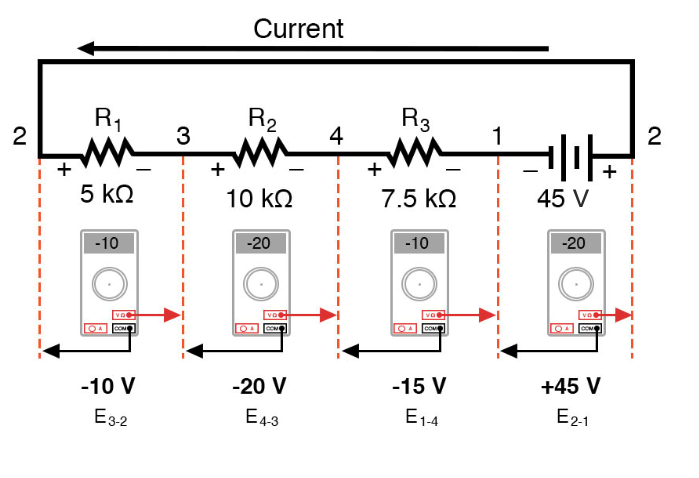
Si nous devions prendre ce même voltmètre et lire la tension sur les combinaisons de composants, en commençant par le seul R₁ sur la gauche et en progressant sur toute la chaîne de composants, nous verrons comment les tensions s'additionnent algébriquement (à zéro) :

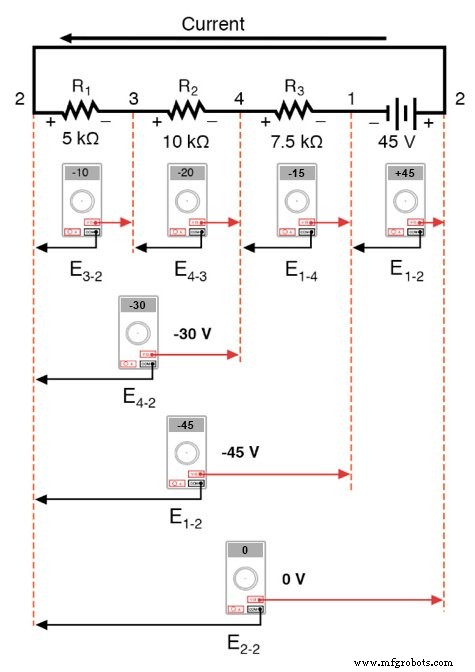
Le fait que les tensions série s'additionnent ne devrait pas être un mystère, mais nous remarquons que la polarité de ces tensions fait une grande différence dans la façon dont les chiffres s'additionnent. Lors de la lecture de la tension aux bornes de R₁ —R₂ , et R₁ —R₂ —R₃ (J'utilise un symbole « double tiret » « - » pour représenter la série connexion entre les résistances R₁ , R₂ , et R₃ ), nous voyons comment les tensions mesurent des amplitudes successivement plus grandes (quoique négatives), car les polarités des chutes de tension individuelles sont dans la même orientation (positive à gauche, négative à droite).

La somme des chutes de tension aux bornes de R₁ , R₂ , et R₃ est égal à 45 volts, ce qui est le même que la sortie de la batterie, sauf que la polarité de la batterie est opposée à celle des chutes de tension de la résistance (négatif gauche, positif droit), nous nous retrouvons donc avec 0 volt mesuré sur l'ensemble de la chaîne de composants.

Que nous devrions nous retrouver avec exactement 0 volt sur toute la chaîne ne devrait pas non plus être un mystère. En regardant le circuit, nous pouvons voir que l'extrême gauche de la chaîne (côté gauche de R₁ :le point numéro 2) est directement connecté à l'extrême droite de la chaîne (côté droit de la batterie :point numéro 2), si nécessaire pour compléter le circuit.

Étant donné que ces deux points sont directement connectés, ils sont électriquement communs l'un à l'autre. Et, en tant que telle, la tension entre ces deux points électriquement communs doit être zéro.

Démonstration de la loi de tension de Kirchhoff dans un circuit parallèle

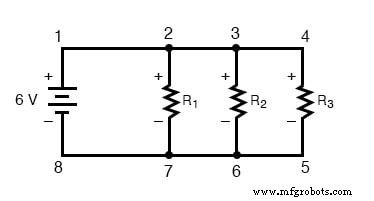
La loi de tension de Kirchhoff (parfois appelée KVL pour faire court) fonctionnera pour n'importe quel configuration de circuit du tout, pas seulement de simples séries. Notez comment cela fonctionne pour ce circuit parallèle :

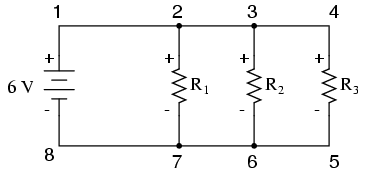
Étant un circuit parallèle, la tension aux bornes de chaque résistance est la même que la tension d'alimentation :6 volts. En additionnant les tensions autour de la boucle 2-3-4-5-6-7-2, nous obtenons :

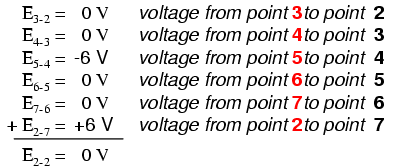
Notez comment j'étiquette la tension finale (somme) comme E_2-2 . Puisque nous avons commencé notre séquence de pas de boucle au point 2 et fini au point 2, la somme algébrique de ces tensions sera la même que la tension mesurée entre le même point (E_2-2 ), qui doit bien entendu être égal à zéro.

La validité de la loi de tension de Kirchhoff, quelle que soit la topologie du circuit

Le fait que ce circuit soit parallèle au lieu d'être en série n'a rien à voir avec la validité de la loi de tension de Kirchhoff. D'ailleurs, le circuit pourrait être une "boîte noire" - sa configuration de composants complètement cachée à notre vue, avec seulement un ensemble de bornes exposées pour nous permettre de mesurer la tension entre - et KVL serait toujours vrai :

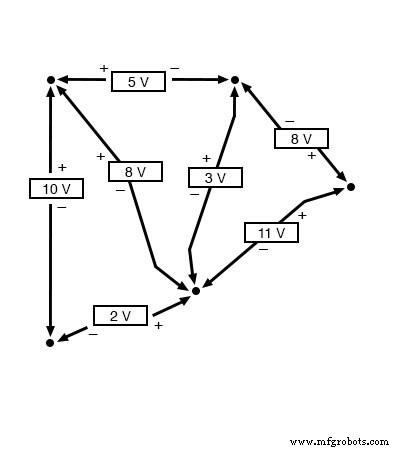
Essayez n'importe quel ordre d'étapes à partir de n'importe quel terminal dans le diagramme ci-dessus, en revenant au terminal d'origine, et vous constaterez que la somme algébrique des tensions toujours est égal à zéro.

De plus, la "boucle" que nous traçons pour KVL n'a même pas besoin d'être un véritable chemin de courant au sens de circuit fermé du terme. Tout ce que nous avons à faire pour nous conformer au KVL est de commencer et de terminer au même point du circuit, en comptabilisant les chutes de tension et les polarités au fur et à mesure que nous allons entre le point suivant et le dernier. Considérez cet exemple absurde, traçant la "boucle" 2-3-6-3-2 dans le même circuit de résistance parallèle :

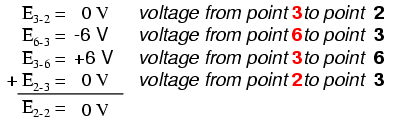
Utilisation de la loi de tension de Kirchhoff dans un circuit complexe

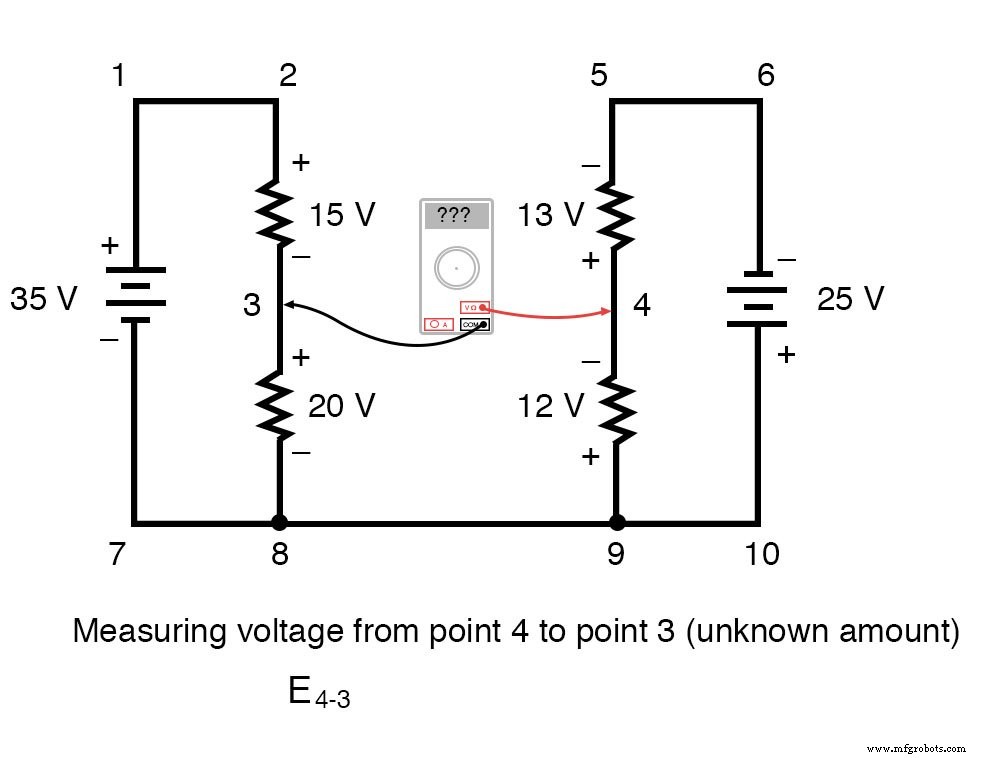
KVL peut être utilisé pour déterminer une tension inconnue dans un circuit complexe, où toutes les autres tensions autour d'une « boucle » particulière sont connues. Prenons comme exemple le circuit complexe suivant (en fait deux circuits en série reliés par un seul fil en bas) :

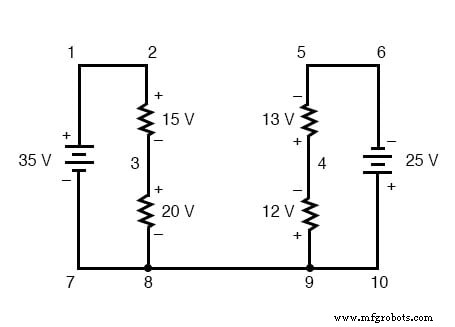
Pour simplifier le problème, j'ai omis les valeurs de résistance et simplement donné des chutes de tension sur chaque résistance. Les deux circuits en série partagent un fil commun entre eux (fil 7-8-9-10), effectuant des mesures de tension entre les deux circuits possibles. Si nous voulions déterminer la tension entre les points 4 et 3, nous pourrions établir une équation KVL avec la tension entre ces points comme inconnue :

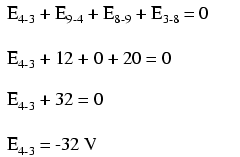
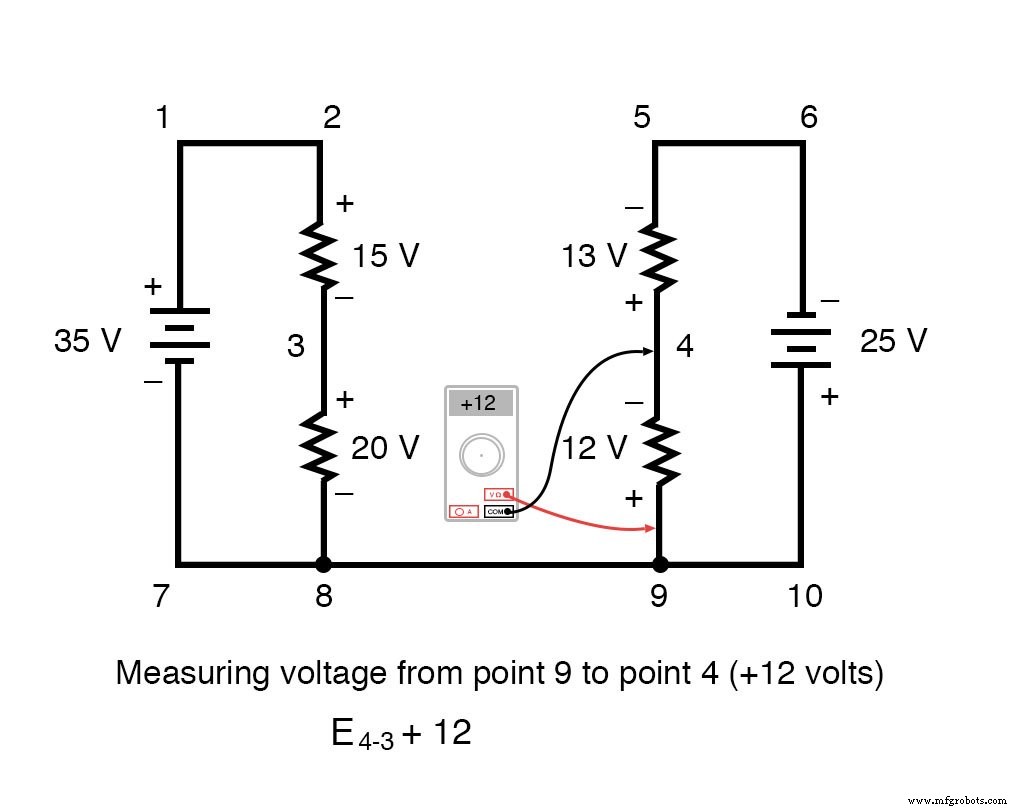
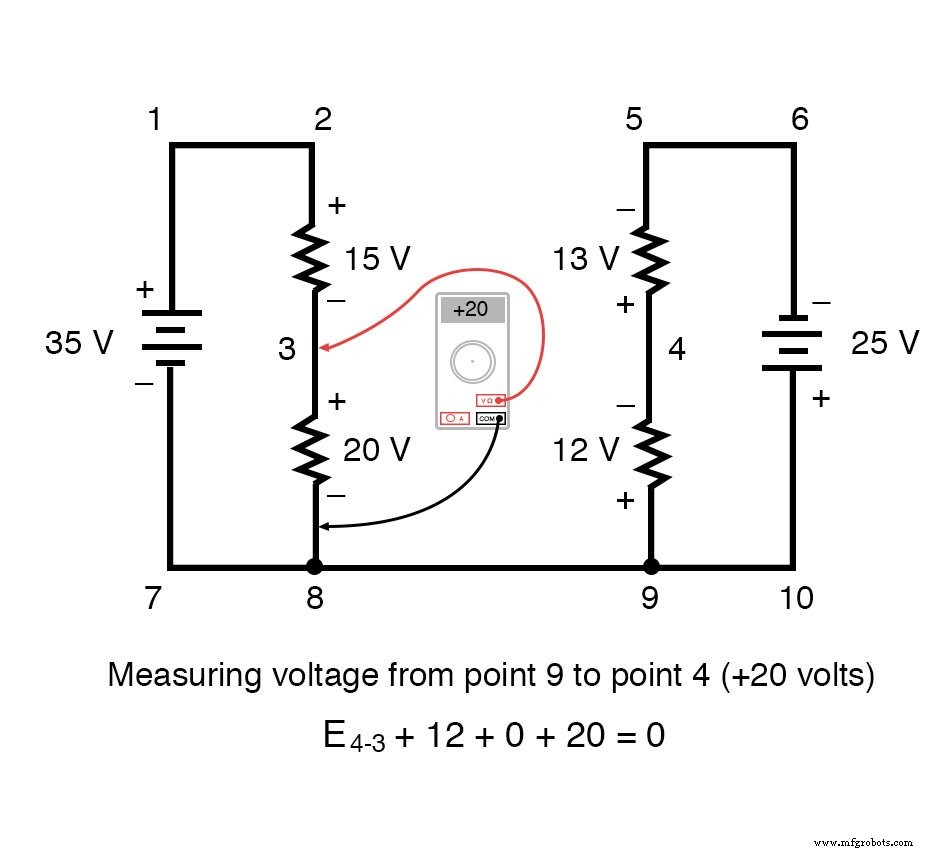
En contournant la boucle 3-4-9-8-3, nous écrivons les chiffres de chute de tension comme un voltmètre numérique les enregistrerait, mesurant avec le fil de test rouge sur le point en avant et le fil de test noir sur le point derrière au fur et à mesure que nous progressons. la boucle. Par conséquent, la tension du point 9 au point 4 est un positif (+) 12 volts car le "fil rouge" est sur le point 9 et le "fil noir" est sur le point 4.

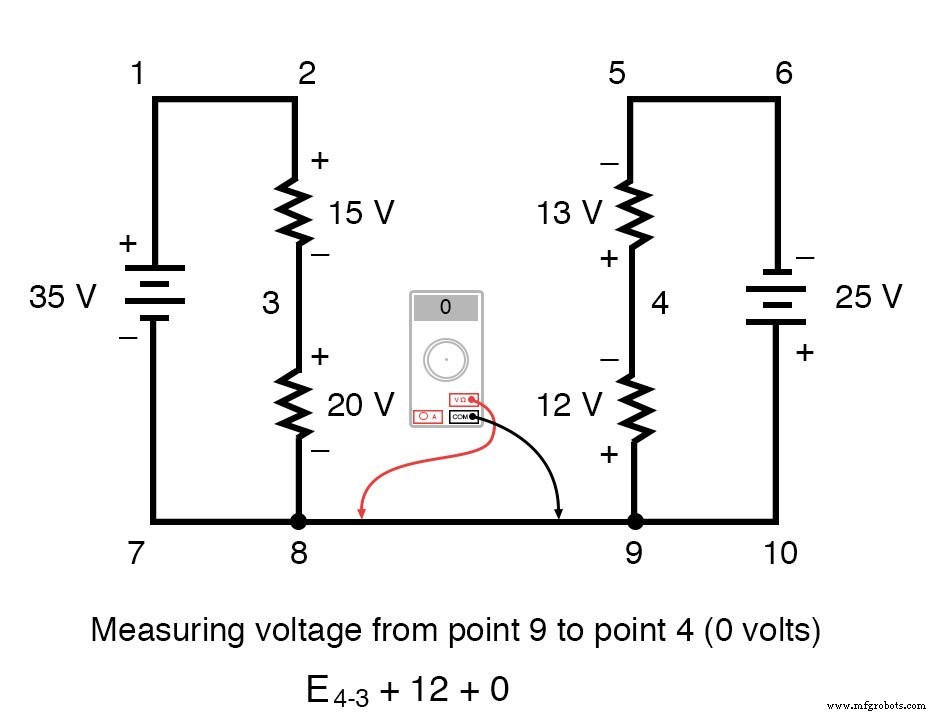
La tension du point 3 au point 8 est un positif (+) 20 volts car le "fil rouge" est au point 3 et le "fil noir" est au point 8. La tension du point 8 au point 9 est de zéro, bien sûr , car ces deux points sont électriquement communs.

Notre réponse finale pour la tension du point 4 au point 3 est un négatif (-) 32 volts, nous indiquant que le point 3 est en fait positif par rapport au point 4, précisément ce qu'un voltmètre numérique indiquerait avec le fil rouge au point 4 et la mine noire au point 3 :

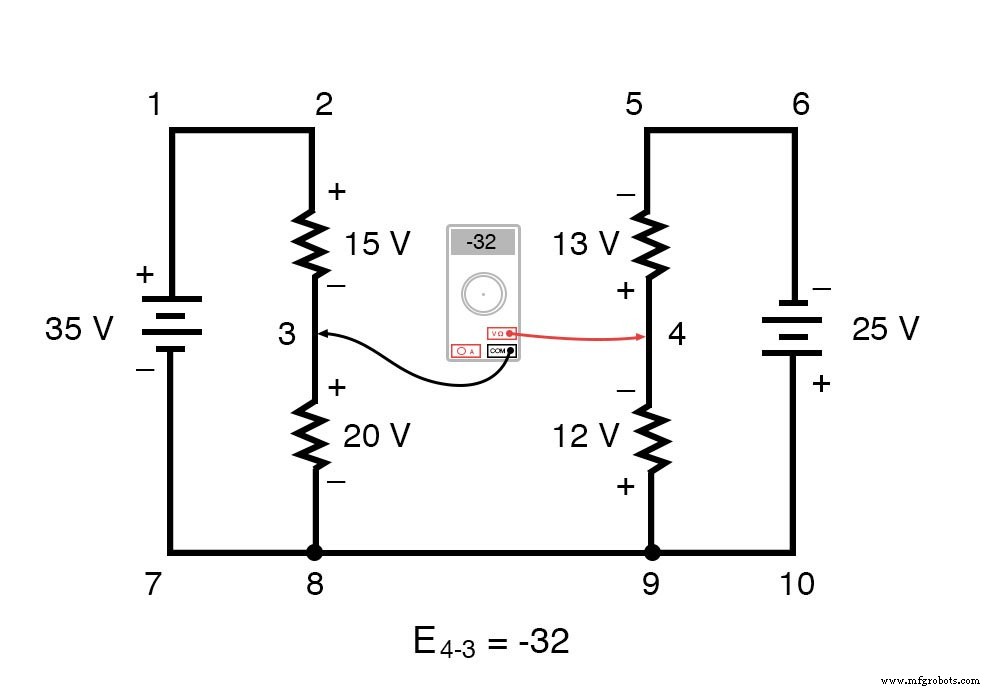
En d'autres termes, le placement initial de nos "fils de compteur" dans ce problème KVL était "en arrière". Avons-nous généré notre équation KVL en commençant par E_3-4 au lieu de E_4-3 , en faisant le tour de la même boucle avec l'orientation opposée du fil de mètre, la réponse finale aurait été E_3-4 =+32 volts :

Il est important de réaliser qu'aucune des deux approches n'est « mauvaise ». Dans les deux cas, on arrive à l'évaluation correcte de la tension entre les deux points, 3 et 4 :le point 3 est positif par rapport au point 4, et la tension entre eux est de 32 volts.

AVIS :

• Loi de tension de Kirchhoff (KVL) :« La somme algébrique de toutes les tensions dans une boucle doit être égale à zéro »

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les lois de Kirchhoff