Caractérisation à l'échelle atomique de la déformation par glissement et usinabilité nanométrique du monocristal 6H-SiC

Introduction

En tant que matériau semi-conducteur de troisième génération à large bande interdite, le SiC présente les caractéristiques d'un champ de claquage élevé, d'une tolérance élevée aux rayonnements, d'une vitesse élevée de saturation des porteurs, d'une conductivité thermique rapide, d'une faible constante diélectrique et de propriétés chimiques stables. de dispositifs optoélectroniques à haute température, haute fréquence, haute puissance, anti-rayonnement et à courte longueur d'onde et intégration optoélectronique [1].

Les cristaux de SiC les plus utilisés sont le 3C, le 4H et le 6H. Les méthodes de traitement telles que le meulage/rodage/polissage restent les principales méthodes lors de l'usinage du SiC monocristallin. Cependant, le rapport de dureté entre le diamant et le SiC est proche de 2:1 (profondeur de traitement < 50 nm)), ce qui est bien inférieur à la valeur recommandée de 5:1 pour le processus d'usinage [2]. L'usure sévère de l'outil de coupe et les dommages du sous-sol influencent directement la qualité de la plaquette. Pour résoudre ces problèmes, de nombreux travaux ont été réalisés pour comprendre le comportement d'élimination du SiC à l'échelle nanométrique. Le mécanisme d'élimination du 3C-SiC et l'influence des facteurs de traitement ont été étudiés de manière approfondie, tels que le mécanisme de déformation plastique pendant le processus de coupe [3,4,5,6,7], l'usure de l'outil [8], le comportement de frottement [9 ], et l'anisotropie du 3C-SiC [10] et l'influence des températures de coupe [11].

Le 6H-SiC a une structure d'empilement ABCACB plus complexe. Bien que le mécanisme d'élimination du 6H-SiC dans le traitement SPDT (tournage au diamant à un point) (tel que l'influence de l'angle de coupe de l'outil sur le processus d'enlèvement de matière [12] et la transition cassante-ductile [13]) soit étudié, la recherche est évidemment moins de 3C-SiC. La bande interdite du 6H-SiC (3 eV) est évidemment supérieure à celle du 3C-SiC (2,3 eV). À l'heure actuelle, le niveau technologique du processus de croissance des tiges 6H-SiC est beaucoup plus élevé que celui du 3C-SiC. Le 6H-SiC est bien plus utilisé dans les applications industrielles que le 3C-SiC. Des dispositifs correspondants ont été appliqués dans des champs à haute fréquence, haute puissance et haute température, tels que le redresseur Schottky, le thyratron et le MOSFET de puissance (Metal-Oxide-Semiconductor Field-Effect Transistor). Pour améliorer la qualité de surface/subsurface usinée du 6H-SiC, le moyen le plus efficace et le plus efficace à l'heure actuelle est de trouver une combinaison appropriée de plan cristallin (surface d'usinage)/orientation du cristal (direction d'usinage) qui convient mieux au processus de 6H -SiC.

L'expérience de grattage et les simulations sont parmi les méthodes les plus courantes et les plus efficaces pour explorer le comportement d'élimination [14, 15]. La recherche sur le mécanisme d'enlèvement de matière pendant le processus de grattage a une grande importance pour le processus d'usinage abrasif réel. La méthode de dynamique moléculaire peut fournir un processus de formation et d'élimination des dommages à l'échelle nanométrique. Par conséquent, la simulation de grattage de la dynamique moléculaire a été utilisée pour analyser le comportement d'élimination du 6H-SiC sous l'influence de l'anisotropie induite par la cristallographie.

Méthodologie

Les simulations de coupe dans cet article ont été réalisées à l'aide d'un simulateur massivement parallèle atomique/moléculaire à grande échelle (LAMMPS) [16]. OIVTO [17] et la méthode d'identification de la structure du diamant [18] ont été utilisés pour la visualisation du modèle et l'identification des défauts dans cette étude. Les implémentations de la modélisation des pièces et des outils dépendaient de LAMMPS sans l'aide d'un autre logiciel. Comme le montrent les figures 1a–c, la pièce et l'outil ont tous deux été définis comme des corps déformables, et le comportement à l'usure a été étudié au cours de la simulation. L'outil et le modèle de pièce ont été divisés en trois parties :une couche atomique limite, une couche atomique thermostatique et une zone d'atomes newtoniens. Afin de maintenir la pièce dans sa position initiale, les atomes de la couche limite à l'extrémité inférieure et droite de la pièce ont été fixés. Les atomes de la couche thermostatique et de la couche newtonienne suivent la deuxième loi de Newton. Une limite périodique a été appliquée le long de y direction. Avant la simulation de grattage, les modèles ont été relaxés par l'ensemble NVE avec la méthode du thermostat de Berendsen. Une période de relaxation de 50 ps a été appliquée avant les simulations de grattage pour obtenir un état d'énergie stable. La forme abrasive est une pyramide triangulaire à couronne sphérique avec un angle bord à bord de 90°. Comme le montre la figure 2, les plans cristallins communs (plan a (plan basal), plan m (plan prismatique) et plan c) pour le 6H-SiC ont été sélectionnés comme surfaces d'usinage. Compte tenu de la symétrie de la structure, les combinaisons plan/orientation suivantes ont été sélectionnées comme surface d'usinage/direction d'usinage :\( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{ 1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right) /\left[1\overline{1}00\right] \), et \( \left(11\overline{2}0\right)/\left[0001\right] \). Les paramètres de traitement de la simulation sont présentés dans le tableau 1. Avant la simulation de grattage, les abrasifs étaient placés sur le côté gauche de la pièce et la pointe abrasive se trouve à 50 Å sous la surface supérieure de la pièce. La distance la plus proche entre les abrasifs et la pièce est de 30 , ce qui est loin de la plage de coupure du potentiel d'interaction. L'abrasif se déplace de l'extrémité libre de la pièce dans le sens positif de x -axe et terminer le processus de grattage.

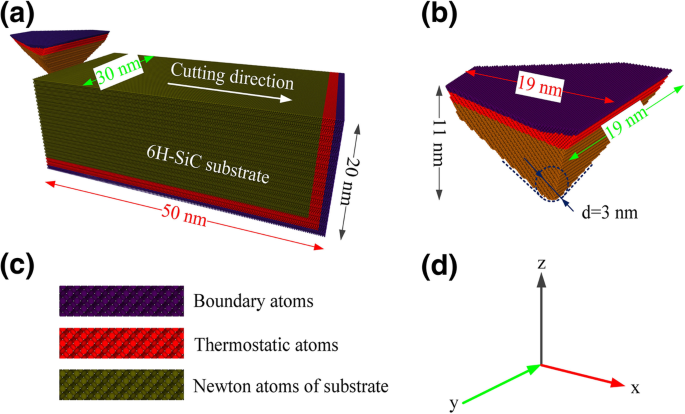
un Modèle MD de simulation de nanoscratching. b La morphologie de l'outil. c Structure du modèle. d Sens de l'axe

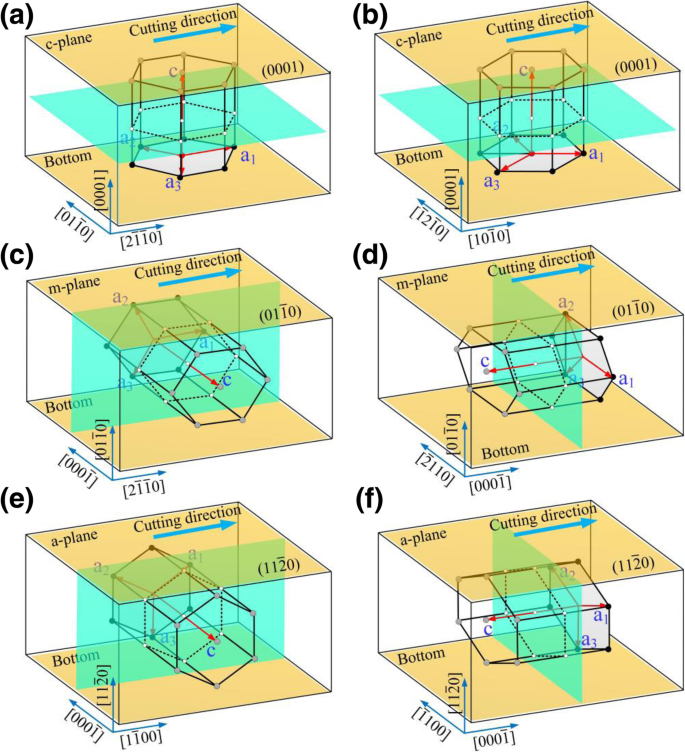
Diagramme schématique du processus de grattage, où a –f sont les modes de traitement correspondants \( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), et \( \left(11\overline{2}0\right)/\left[0001\right] \), respectivement

La fonction de potentiel atomique joue un rôle crucial dans la précision et la fiabilité de la simulation de la dynamique moléculaire. D'après les tests et simulations précédents pour les propriétés mécaniques et les mécanismes d'élimination du SiC monocristallin, la fonction de potentiel d'ordre de liaison analytique (ABOP) proposée par Erhart et Albe [19] est plus adaptée aux interactions pour le silicium et le carbone. Les paramètres utilisés dans la fonction de potentiel sont présentés dans le tableau 2 [19]. Au lieu de la fonction d'énergie potentielle de Tersoff [6], la fonction de potentiel ABOP est utilisée pour définir les interactions Si-Si, CC et Si-C dans et entre l'outil et la pièce pendant le traitement [2, 7, 8, 10, 11].

Résultats et discussion

Analyse d'usinabilité nanométrique

Comme le montrent les Fig. 3 et 4, l'anisotropie du 6H-SiC a eu un impact significatif sur l'usinabilité nanométrique (profondeur usinée, mode d'enlèvement, quantité d'enlèvement et profondeur d'endommagement souterrain (SSD), etc.). Selon la relation surface d'usinage/sens d'usinage et plan de base/c -axe (voir Fig. 3), les modes de traitement des matériaux peuvent être divisés en trois catégories :(i) le plan de base est sélectionné comme surface d'usinage, (ii) le plan de base est perpendiculaire à la surface d'usinage et c -l'axe est perpendiculaire à la direction d'usinage, et (iii) le c -l'axe est parallèle au sens d'usinage.

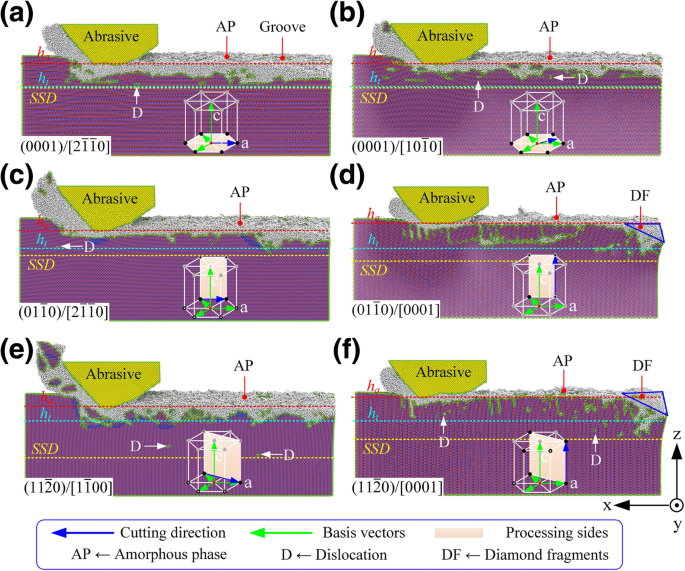
Topographie de la surface usinée sous différentes conditions de plan/orientation cristallines, où a –f sont les modes de traitement correspondants \( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), et \( \left(11\overline{2}0\right)/\left[0001\right] \), respectivement

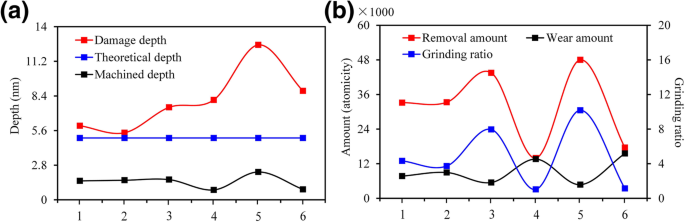
Usinabilité nanométrique dans différentes conditions de plan/orientation du cristal, a l'influence de l'anisotropie sur la profondeur usinée et la profondeur d'endommagement, b l'influence de l'anisotropie sur la quantité d'enlèvement, la quantité d'usure et le rapport de broyage. 1, 2, 3, 4, 5 et 6 sont les méthodes de traitement correspondantes \( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/ \left[10\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\ overline{1}00\right] \) et \( \left(11\overline{2}0\right)/\left[0001\right] \), respectivement. La profondeur de la couche endommagée fait référence à la profondeur maximale des défauts internes du cristal causés par les rayures. La profondeur théorique se réfère à la profondeur prédéfinie avant le traitement. La profondeur usinée fait référence à la profondeur résiduelle après le grattage. La quantité d'enlèvement fait référence au nombre d'atomes dont le matériau de la pièce est enlevé. La quantité d'usure fait référence à la différence du nombre d'atomes des grains abrasifs avant et après le grattage

(i) Comme le montrent les figures 3a, b, l'usinabilité nanométrique du 6H-SiC était extrêmement similaire lorsque le mode de traitement était sélectionné comme \( (0001)/\left[2\overline{1}\overline{1}0 \right] \) et \( (0001)/\left[10\overline{1}0\right] \). Cependant, le processus de suppression du 6H-SiC était plus orienté vers le mode fragile lorsque le mode de traitement était sélectionné comme \( (0001)/\left[10\overline{1}0\right] \). (ii) Comme le montre la figure 3c, e, lorsque les modes de traitement ont été sélectionnés comme \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0 \right] \) et \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), la profondeur usinée et la quantité d'enlèvement de matière étaient significativement plus élevées que celles dans les autres méthodes de traitement. Comme le montre la figure 4, sous la même profondeur de traitement théorique (h _t =5,0 nm), le taux d'enlèvement de matière dans le mode de traitement \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) était 3,4 fois supérieur à que dans le mode de traitement \( \left(01\overline{1}0\right)/\left[0001\right] \). Le rapport de traitement du matériau (quantité d'enlèvement de matière/usure de l'outil) était de 10,1, mais le SSD sous ce paramètre de traitement était également beaucoup plus élevé que celui dans d'autres conditions de traitement, atteignant 2,3 fois de \( (0001)/\left[10\overline{ 1}0\droit] \). Il y avait un grand nombre de nanocristallites sur les surfaces usinées et les puces. Un grand nombre de ruptures fragiles se sont produites dans cette condition. Le mode de traitement \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) ne convient qu'au traitement nanosillon qui nécessite une efficacité de traitement élevée mais est insensible à la dommages souterrains. Le taux d'enlèvement de matière de \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) était similaire à celui de \( \left (11\overline{2}0\right)/\left[1\overline{1}00\right] \) mais le SSD ne représentait que 50% de ce dernier. De plus, l'épaisseur de la couche amorphe sur la surface usinée était bien inférieure à celle de \( (0001)/\left[2\overline{1}\overline{1}0\right] \) et \( (0001) /\left[10\overline{1}0\right] \). La distribution de phase sous la surface était uniforme et les propriétés mécaniques de l'ensemble du sillon étaient meilleures que celles des autres méthodes de traitement. Par conséquent, le mode de traitement \( \left(01\overline{1}0\right)/\left[0001\right] \) est le meilleur choix pour le traitement de micro-nano rainures sur une surface 6H-SiC avec une efficacité élevée , haute précision et faible SSD. (iii) Comme le montrent les Fig. 3d, f, lorsque la direction d'usinage était parallèle à c -axe, la pointe a été fortement usée pendant la phase de traitement initiale. Bien que la profondeur usinée et le taux d'enlèvement de matière aient été bien inférieurs à ceux des autres méthodes de traitement et que le rapport de traitement de matière n'était que d'environ 1,0, le SSD de \( \left(01\overline{1}0\right)/\left[ 0001\right] \) et \( \left(11\overline{2}0\right)/\left[0001\right] \) les modes de traitement étaient supérieurs à celui de \( \left(01\overline{1} 0\right)/\left[2\overline{1}\overline{1}0\right] \). Par conséquent, il n'est pas recommandé d'utiliser \( \left(01\overline{1}0\right)/\left[0001\right] \) et \( \left(11\overline{2}0\right)/ \left[0001\right] \) dans le traitement de micro-nano rainures à la surface du 6H-SiC. Cependant, ces modes démontrent une excellente résistance à l'usure; par conséquent, ils sont adaptés à la face de coupe de l'outil de coupe SiC monocristallin, qui a de larges perspectives dans le domaine du traitement ultra-précis des métaux ferreux.

Analyse du mouvement des lèvres et de la distribution des dommages sous la surface

Répartition des facteurs de Schmid dans le processus de grattage basée sur une pointe de pyramide triangulaire

Les systèmes de glissement courants du système cristallin hexagonal (voir Fig. 4) comprennent principalement le glissement basal, le glissement prismatique et le glissement pyramidal. La résistance au glissement est liée à l'énergie de défaut d'empilement généralisé (GSF) et dE _GSF /dx contre (x /b ) des systèmes de glissement. Le mouvement de glissement se produirait sur le plan le plus dense et le long de la direction la plus courte [10]. Les systèmes de glissement préférentiels dans le glissement basal sont le glissement basal (jeux aléatoires)/<\( 1\overline{1}00 \)> et le glissement basal (jeux aléatoires)/<\( 11\overline{2}0 \)> [20]. Comme le premier manque d'un minimum d'énergie intermédiaire, le second est prioritaire dans les simulations et les expériences [20]. Par conséquent, les mouvements de glissement considérés dans ce travail sont les suivants :glissement basal (shuffle sets)/<\( 11\overline{2}0 \)> et glissement prismatique et glissement. Figure 5.

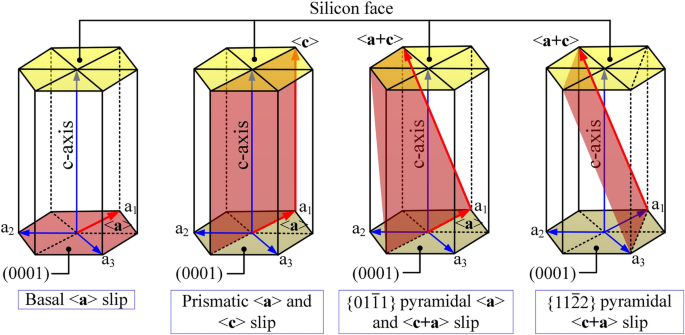
Systèmes de glissement du système hexagonal

La composante de contrainte de cisaillement sur le plan de glissement τ _s peut être calculé par la relation :

$$ {\tau}_{\mathrm{ss}}={\sigma}_{\mathrm{cont}}\mathit{\cos}<\overset{\rightharpoonup }{f},\overset{\rightharpoonup } {n_g}>\cos <\overset{\rightharpoonup }{f},\overset{\rightharpoonup }{t_g}>={\sigma}_{\mathrm{cont}}\bullet m $$ (1)

où σ _suite est la contrainte de contact, \( \overset{\rightharpoonup }{f} \) est la direction de chargement, \( \overset{\rightharpoonup }{n_g} \) et \( \overset{\rightharpoonup }{t_g} \) sont la normale au plan de glissement et la direction de glissement dans le système de coordonnées cartésien global, et m est le facteur de Schmid. Le système de coordonnées global a été fixé et le système de coordonnées local a tourné avec la direction du cristal. Le x -l'axe du système de coordonnées local était parallèle au vecteur de base \( \overset{\rightharpoonup }{a_1} \) tandis que le z -axis était parallèle au vecteur de base \( \overset{\rightharpoonup }{c} \).

Pendant le processus de grattage, la face de contact principale de la pointe de la pyramide triangulaire était la face de coupe, mais lorsque l'outil s'est fortement usé, la face de contact principale a transité vers le composé de la face de coupe et de la pointe. La direction de chargement correspondante \( \overset{\rightharpoonup }{f} \) est présentée comme

$$ \left\{\begin{array}{c}\overset{\rightharpoonup }{f_1}=\left({f}_{1x},{f}_{1y},{f}_{1z} \right)\kern8em \mathrm{rake}\ \mathrm{face}\ \\ {}\overset{\rightharpoonup }{f_2}=\left({f}_{2x},{f}_{2y}, {f}_{2z}\right)\kern9.75em \mathrm{tip}\ \mathrm{top}\end{array}\right. $$ (2)

où \( \overset{\rightharpoonup }{f_1}=\left(1,0,-\sqrt{2}\right) \), \( \overset{\rightharpoonup }{f_2}=\left(0,0 ,-1\right) \) dans le système de coordonnées global.

En tant que système cristallin hexagonal, le système de glissement du 6H-SiC peut être exprimé sous la forme {h k i l }/ < u v t w>. Le plan de glissement normal \( \overset{\rightharpoonup }{n_c} \) et la direction de glissement \( \overset{\rightharpoonup }{t_c} \) dans le système de coordonnées cartésien local sont indiqués par

$$ \overset{\rightharpoonup }{n_c}=\left(\frac{3}{2}h,\frac{\sqrt{3}}{2}\left(h+2k\right),\frac{ 3 la}{2c}\right) $$ (3) $$ \overset{\rightharpoonup }{t_c}=\left(u-\frac{1}{2}\left(v+t\right),\ frac{\sqrt{3}}{2}\left(vt\right),\frac{c}{a}w\right) $$ (4)

Le plan de glissement normal \( \overset{\rightharpoonup }{n_g} \) et la direction de glissement \( \overset{\rightharpoonup }{t_g} \) dans le système de coordonnées cartésien global sont indiqués par

$$ \overset{\rightharpoonup }{n_g}=T\bullet \overset{\rightharpoonup }{n_c} $$ (4) $$ \overset{\rightharpoonup }{t_g}=T\overset{\rightharpoonup }{\ puce {t}_c} $$ (5)

où la matrice de rotation forme du système de coordonnées global au système de coordonnées local et les angles de rotation correspondants sont indiqués dans le tableau 3

D'après les formules (1) à (5), les facteurs de Schmid des systèmes de glissement correspondants lorsque les directions de chargement étaient \( \overset{\rightharpoonup }{f_1} \) et \( \overset{\rightharpoonup }{f_2} \ ) sont présentés dans le tableau 4. (i) La valeur c/a du 6H-SiC a atteint 4,901, ce qui est bien supérieur à 1,633. Par conséquent, la contrainte de cisaillement critique requise pour le glissement basal était inférieure à celle du système de glissement prismatique. Lorsque la surface usinée était un plan basal, le coefficient de système de glissement basal était plus élevé que celui des autres systèmes de glissement. Par conséquent, lorsque les modes de traitement ont été sélectionnés comme \( (0001)/\left[2\overline{1}\overline{1}0\right] \) et \( (0001)/\left[10\overline{1 }0\right] \), le mouvement de glissement basal a eu lieu en premier. (ii) Lorsque les modes de traitement ont été sélectionnés comme \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) et \( \ left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), en ne considérant que les directions de chargement \( \overset{\rightharpoonup }{f_1} \) et \( \overset{\rightharpoonup }{f_2} \), il était théoriquement impossible que le glissement basal se produise, et le mouvement de glissement prismatique a pris le pas. (iii) Lorsque les modes de traitement ont été sélectionnés comme \( \left(01\overline{1}0\right)/\left[0001\right] \) et \( \left(11\overline{2}0\right )/\left[0001\right] \), comme le montre la figure 4, le tip-top a été sérieusement usé pendant la phase de traitement initial et \( \overset{\rightharpoonup }{f_2} \) a joué un rôle crucial dans le processus de grattage. Par conséquent, le mouvement de glissement se produirait dans le système de glissement prismatique symétriquement distribué avec le plan YOZ dans les coordonnées globales.

Répartition des dommages de surface/subsurface

Comme le montre la figure 6a, b lorsque \( (0001)/\left[2\overline{1}\overline{1}0\right] \) et \( (0001)/\left[01\overline{1 }0\right] \) ont été sélectionnés, le mouvement de glissement s'est principalement produit sur le système de glissement \( (0001)/<1\overline{2}10> \), qui est dû à la poussée vers l'avant de l'outil. Le mode de mouvement de glissement correspondant est cohérent avec les résultats du calcul du coefficient de Schmidt. Il y avait des grains nanocristallins et des déflexions de réseau dans la zone souterraine et ces dommages ont formé des zones de distorsion de réseau irrégulières. La phase amorphe couvrait toute la surface usinée et la profondeur de la dislocation était proche de la profondeur de la couche de distorsion du réseau.

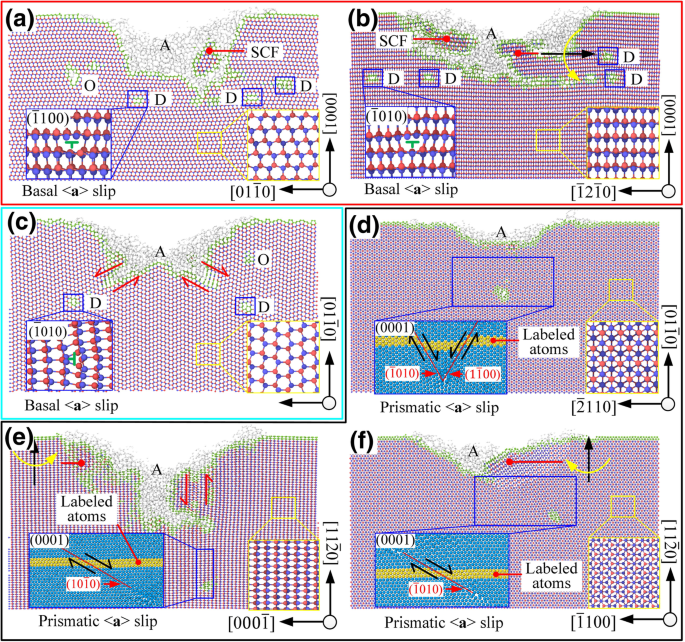
La section transversale de la zone usinée, D est la luxation, A est une phase amorphe, SCF est une forme monocristalline, O est un autre type de défaut, où a –f sont les modes de traitement correspondants \( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), et \( \left(11\overline{2}0\right)/\left[0001\right] \), respectivement.

Lorsque \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) est sélectionné, comme coefficient de Schmidt de basal < a> le glissement est égal à 0, le basal <a> le glissement ne devrait pas se produire en théorie. Mais l'angle entre la direction de chargement \( \overset{\rightharpoonup }{f_1} \) et la direction de glissement \( \left[11\overline{2}0\right] \) n'était que de 5,3°. Sous l'action de cisaillement due au mouvement relatif entre la zone de contact et la zone de non-contact (voir Fig. 6c), la base <a> le glissement a été déclenché avant le glissement prismatique sous le mode de traitement de \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) et s'est produit des deux côtés de la rainure en V. Sous le mode de traitement de \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \), les angles entre la direction de chargement \( \overset{\rightharpoonup }{f_1} \) et les directions de glissement \( \left[1\overline{2}10\right] \) et \( \left[\overline{1}\overline{1}20\right] \) étaient 24,7° et 35,3°, respectivement. L'action de cisaillement n'a pas induit de mouvement de glissement du plan basal. Le mode de mouvement de glissement correspondant est cohérent avec les résultats du calcul du coefficient de Schmidt. Comme le montre la figure 6e, lorsque \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) a été sélectionné, le système de glissement \( \left[ 1\overline{2}10\right]/\left(\overline{1}010\right) \) avait un coefficient de Schmidt élevé sous l'action conjointe de \( \overset{\rightharpoonup }{f_1} \) et \ ( \overset{\rightharpoonup }{f_2} \), ce qui entraînerait inévitablement une grande profondeur de la couche d'endommagement du sous-sol. La distorsion du réseau et la phase amorphe existaient également, mais contrairement à l'usinage sur le plan basal, la profondeur de dislocation était significativement supérieure à celle de la distorsion du réseau. Le sp ³ →sp ² le comportement de transition s'est produit dans la région souterraine.

Lorsque la direction de traitement était parallèle au c -axe, en raison de l'usure sévère de la pointe, le glissement prismatique causé par l'extrusion vers le bas était le principal mode de mouvement de glissement dans l'étape de grattage stable. Le mode de mouvement de glissement correspondant était cohérent avec les résultats du calcul du coefficient de Schmidt. Lorsque \( \left(01\overline{1}0\right)/\left[0001\right] \) a été sélectionné, avec la direction de chargement \( \overset{\rightharpoonup }{f_2} \), les systèmes de glissement \( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) et \( \left[\overline{1}\overline{1}20\right] /\left(1\overline{1}00\right) \) avait le même coefficient de Schmidt, un glissement croisé s'est produit sur les deux surfaces de glissement avec un angle de 60°, puis, l'effet d'épinglage s'est produit qui a entravé le mouvement de glissement . Ainsi, la profondeur maximale des dommages souterrains SSD _max serait inférieur ou égal à h _t bronzage θ /2 cot α /2, où θ = 101° est l'angle théorique du nanosillon et α = 60° est l'angle entre le plan de glissement \( \left(\overline{1}010\right) \) et \( \left(1\overline{1} 00\droit) \). Lorsque \( \left(11\overline{2}0\right)/\left[0001\right] \) a été sélectionné, les systèmes de glissement \( \left[\overline{2}110\right]/\left( 0\overline{1}10\right) \) et \( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) avaient également le même coefficient de Schmidt, mais le mouvement de glissement a été affecté par l'usure irrégulière de la pointe et seul le système de glissement \( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) s'est produit.

En résumé, comme le montre la figure 7, les dommages dans les régions souterraines dans différentes conditions de traitement étaient principalement des dislocations, une distorsion du réseau (torsion/glissement relatif) et une phase amorphe. La déformation du 6H-SiC était principalement causée par le mouvement de glissement, la non-cristallisation des matériaux et la distorsion irrégulière du réseau. Les principaux modes de déformation du glissement étaient le glissement basal et le glissement prismatique, qui sont étroitement liés à la surface/direction de traitement.

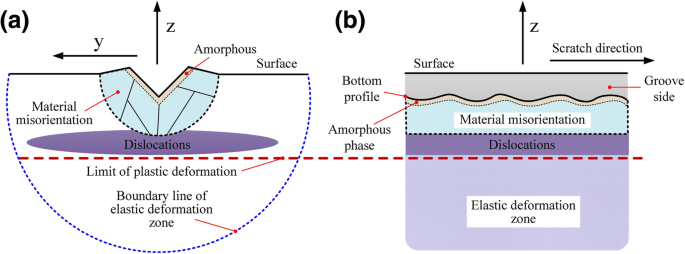
Répartition des dommages de surface/subsurface traités. un xy la Coupe transversale. b xz coupe transversale