Réévaluation des distributions de la durée de vie de la luminescence dans les nanocristaux de silicium

Introduction

Les nanoparticules colloïdales peuvent être utilisées dans une multitude d'applications, notamment la catalyse, les traitements médicaux et les applications optoélectroniques [1,2,3,4]. Les nanoparticules semi-conductrices sont particulièrement intéressantes pour les applications d'émission de lumière, photovoltaïques et photocatalytiques [5, 6]. Les nanocristaux de silicium (SiNCs) sont actuellement au centre de l'attention en raison des propriétés d'émission accordables [7] ainsi que de l'abondance et de la biocompatibilité du silicium [8]. Afin de développer des technologies basées sur les nanoparticules, une connaissance approfondie des propriétés optoélectroniques pertinentes est nécessaire, et la spectroscopie à résolution temporelle est souvent un outil précieux à cette fin.

Les durées de vie de luminescence des SiNC sont généralement modélisées avec une fonction exponentielle étirée (SE) ayant la forme de base exp[ − (λt ) ^β ], où le paramètre de dispersion β prend des valeurs entre 0 et 1, λ est un paramètre de taux, et t est le temps. Cette fonction est souvent décrite comme « plus lente qu'exponentielle » et implique une distribution asymétrique des taux de décroissance se prolongeant vers des durées de vie plus longues. Une fois le β et λ ont été trouvés en ajustant une courbe de décroissance de la luminescence, la distribution du taux de décroissance correspondante peut être approximativement reconstruite [9].

L'origine de la décroissance de la luminescence SE dans le silicium et d'autres points quantiques semi-conducteurs a été fortement débattue au cours des deux dernières décennies, et le débat s'est poursuivi récemment [10]. Diverses explications ont été proposées pour l'apparition de la SE dans la dynamique de désintégration, y compris l'effet tunnel et le piégeage des porteurs dans des ensembles de nanocristaux étroitement espacés [11], la distribution de taille élargie de manière non homogène [12], le couplage électron-phonon dépendant de la taille [10] , et une distribution des hauteurs de barrière pour la recombinaison non radiative [13], cette dernière étant similaire à une suggestion précédente pour le silicium poreux [14]. De toute évidence, la connaissance de la distribution de taux est nécessaire pour comprendre le mécanisme de luminescence dans les SiNC ainsi que dans les nanocristaux semi-conducteurs plus généralement.

Dans une grande partie de la littérature précédente sur les SiNC, la décroissance exponentielle étirée était supposée a priori, généralement sans analyse d'autres distributions possibles. Le SE a tendance à bien s'adapter visuellement (c'est-à-dire que la ligne la mieux ajustée semble bien correspondre aux données « à l'œil »). De plus, dans la grande majorité des travaux précédents, par exemple [15], il y a un manque de clarté quant à savoir si la décroissance de la population ou la décroissance de la luminescence est réellement modélisée. Ceux-ci sont liés par une dérivée et il faut utiliser l'expression correcte afin de comprendre les échelles de temps de décroissance dans l'échantillon [16]. En outre, la fonction de réactivité du détecteur peut avoir un effet significatif sur la courbe de décroissance de la luminescence mesurée dans les SiNC, en raison du large spectre d'émission d'ensemble. Malgré cela, la réactivité a rarement, voire jamais, été prise en compte, ce qui rend difficile la comparaison des résultats de différentes enquêtes. Enfin, aucune étude antérieure n'a tenté d'utiliser la spectroscopie à résolution de fréquence (FRS) dans l'analyse des nanocristaux de silicium. En principe, FRS permet d'extraire la distribution de la durée de vie sans supposer de modèle a priori.

Le but de cet article est d'établir une approche pour mesurer, modéliser et interpréter la dynamique de luminescence des nanocristaux de silicium. On espère que cela pourrait aider à mieux comprendre la grande diversité de résultats souvent contradictoires dans la littérature, conduire à un meilleur accord, ou du moins plus de cohérence, entre les différentes mesures, et à mieux comprendre les mécanismes de luminescence.

Théorie de base

Nous comparons trois modèles :l'exponentielle étirée, qui est largement utilisée pour les nanocristaux de Si, la distribution de désintégration lognormale, qui a été appliquée pour la première fois aux SiNCs récemment [17], et la désintégration bimoléculaire. Pour tout modèle, la fonction de densité de probabilité d'émission, représentée par l'intégrale de la fonction d'intensité g (t ), à l'instant t′ est lié à la fraction d'excitations restant à t′ selon [16].

où c _t et c ₀ sont le nombre de NC excités au temps t et initialement. La fonction de densité de probabilité décrit la fraction de photons émis entre l'instant 0 et t par rapport au nombre total de photons émis. Si la décroissance de la population suit une équation de taux de premier ordre (c'est-à-dire une recombinaison "monomoléculaire"), nous avons dc _t /dt = − λc _t , où λ = 1/τ ₀ , conduisant à l'habituel c _t /c ₀ = exp[− λt ] et g (t ) = λ⋅ exp[− λt ] après avoir pris la dérivée temporelle des deux côtés de l'équation. 1. La dérivée est nécessaire car l'intensité de luminescence mesurée dans la fenêtre dt′ est proportionnel à la variation de la fraction excitée sur cet intervalle.

Si nous considérons à la fois les taux radiatifs et non radiatifs, alors nous remplaçons le taux de décroissance total λ avec λ _R + λ _NR de sorte que g (t ) = (λ _R + λ _NR )exp[− (λ _{R +} λ _NR t ] = λ _R exp[− (λ _{Ri +} λ _NR )t ] + λ _NR exp[− (λ _{R +} λ _NR )t ] dans lequel seul le premier terme est mesurable, ce qui donne une intensité mesurée pour la spectroscopie résolue en temps (TRS) donnée par

La fonction de décroissance utilisée pour ajuster les données, I _t = A· exp(− λt ) + dc, échelles avec un préfacteur arbitraire supplémentaire, A , qui dépend de l'efficacité de détection et du nombre de nanoparticules excitées et conduira à l'échelle appropriée. Un décalage en courant continu est généralement ajouté à la fonction de décroissance en tant qu'autre paramètre d'ajustement.

Dans le cas de la décroissance exponentielle étirée, la fraction d'émetteurs excités décroît selon

où λ _SE est le taux de décroissance exponentielle étirée (égal à 1/τ _SE ). L'insertion dans l'Eq. 1 et en prenant la dérivée des deux côtés comme précédemment donne une fonction de probabilité d'émission donnée par

Un moyen d'estimer la distribution des fréquences H (λ ) qui conduit à l'équation. 3 a été montré en utilisant une transformée de Laplace inverse [9], donnant une distribution qui s'élargit avec la diminution de β et est biaisé vers les hautes fréquences.

Malheureusement, dans l'éq. 4, il n'est pas possible de séparer le préfacteur en parties radiative et non radiative. Cela signifie que l'équation. 4 est correctement normalisé uniquement pour λ _NR = 0 [16], et la distribution de durée de vie obtenue à partir d'une courbe de décroissance PL n'est comprise que de cette manière. De plus, il y a un terme dépendant du temps dans le préfacteur; par conséquent, la décroissance de la population a une dépendance temporelle différente de celle de la décroissance de la luminescence [16, 18]. Pour obtenir les valeurs de τ _SE et β pour la décroissance de la population à partir de laquelle les durées de vie moyennes appropriées peuvent être extraites, il faut utiliser l'équation. 4 pour modéliser la décroissance observée, où l'on remplace g (t ) par la fonction de décroissance mesurée I _t :

Dans l'éq. 5, un paramètre de mise à l'échelle (qui peut également absorber le β et λ termes dans le préfacteur) et un décalage continu ont été insérés comme paramètres d'ajustement. La durée de vie moyenne est donnée par

où Γ représente la fonction Gamma, et le temps de décroissance moyen est

Dans de nombreux travaux antérieurs, il était courant d'utiliser l'exponentielle étirée « standard » exp[− (λ _SE t ) ^β ] pour modéliser la décroissance de la luminescence au lieu de la décroissance de la population. En conséquence, nous avons une fonction d'intensité normalisée donnée par

L'équation 8 est normalisée de sorte que l'intégration entre t = 0 et ∞ est égal à 1. Le modèle d'ajustement correspondant est simplement

L'équation 9 est largement appliquée et s'adapte souvent assez bien aux données de luminescence SiNC, malgré le fait que (comme l'équation 4) Eq. 8 est strictement normalisé pour une efficacité quantique absolue (AQY) de 100 %. Un point souvent négligé est le fait que l'on ne peut pas extraire τ _SE (=1/λ _SE ) et β à partir de la décroissance de la luminescence modélisée par l'Eq. 9 et les utiliser pour calculer les temps moyens avec les équations. 6 et 7. Essentiellement, les équations. 4 et 8 sont des modèles de décroissance d'intensité différents et il faut s'attendre à des fonctions de décroissance de la population, des temps moyens et des distributions de taux de décroissance différents.

Afin de trouver la décroissance de la population qui conduirait à une fonction d'intensité donnée par l'équation. 9, nous appliquons le même processus que nous avons fait pour obtenir de l'Eq. 4 à Éq. 5, mais à l'envers, c'est :

Après plusieurs étapes, la solution de l'Eq. 10 est

L'équation 11 est la décroissance de la population obtenue à partir de la décroissance de l'intensité donnée par l'équation. 8. Trouver la durée de vie moyenne de la manière habituelle conduit à

et un temps de décroissance moyen de

Enfin, la distribution de fréquence est (1 /λ )·H (λ ), où, comme précédemment, H (λ ) est la distribution calculée dans la réf. [9] pour une décroissance de population donnée par l'équation. 3. Ces résultats sont résumés dans le tableau 1.

Les différences entre les deux formules SE sont significatives (Fig. 1). Dans la littérature, on trouve fréquemment que la décroissance d'intensité est modélisée par A· exp[− (t /τ _SE ) ^β ] + dc (c'est-à-dire, Eq. 9) puis les temps moyens sont calculés en utilisant les Eqs. 6 et 7. Cela semble être mathématiquement incorrect, puisque les Eqs. 6 et 7 sont dérivés d'une décroissance d'intensité donnée par l'Eq. 4, pas l'Éq. 8. Par exemple, prendre τ _SE = 100 s et β = 0.7, comme le montre la Fig. 1, pour une décroissance d'intensité donnée par exp[− (t /τ _SE ) ^β ], nous trouvons une constante de temps moyenne de 199 µs (Eq. 12), contre 127 µs en utilisant l'Eq. 6. Des différences similaires sont trouvées pour les temps de décroissance moyens (équations 7 et 13). De plus, il existe une approche connue sous le nom de méthode de Higashi-Kastner pour estimer une durée de vie caractéristique [19], qui a été appliquée aux SiNC comme alternative à l'application du modèle de désintégration SE [20, 21]. Dans ce modèle, le temps de retard caractéristique, t _d , est simplement considéré comme le pic des données de décroissance tracé comme I _t ·t contre t . Cela a été suggéré comme étant équivalent à (1 /β ) ^{1 /β} ·τ _SE obtenu à partir de l'éq. 9 [20].

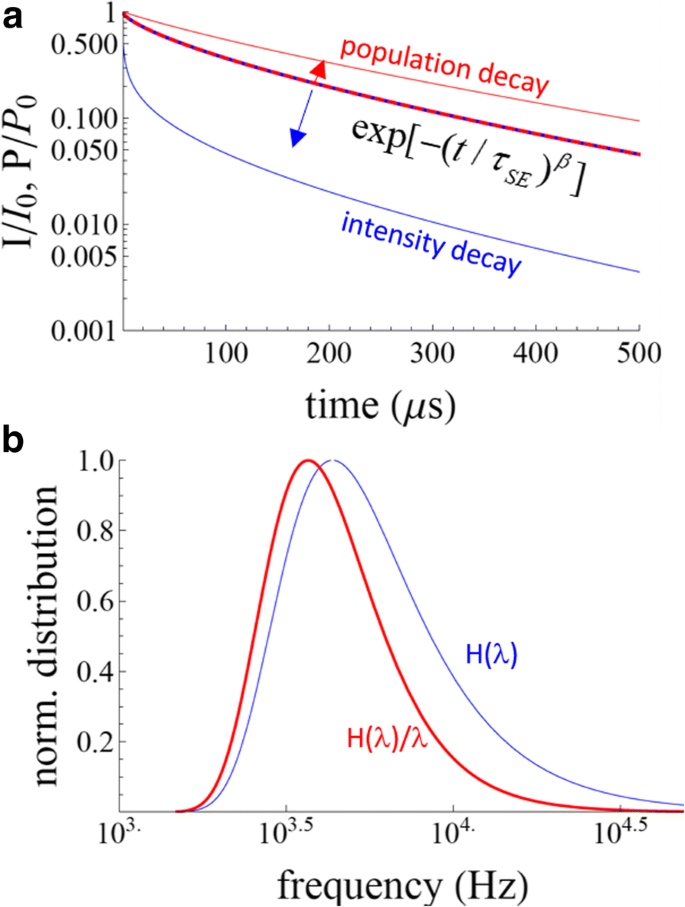
Les exponentielles étirées. un La population et l'intensité diminuent pour la fonction exponentielle étirée avec τ _SE = 100 s et β = 0,7. La ligne pointillée bleu-rouge est exp[− (λt ) ^β ]. Si cela représente la décroissance de la population, la décroissance d'intensité sera donnée par la ligne bleue. Si exp[− (λt ) ^β ] est la décroissance de l'intensité, puis la décroissance de la population est indiquée par la ligne rouge. b Les répartitions tarifaires correspondantes

Alternativement, la distribution des taux de décroissance peut suivre un Η spécifique (λ ), conduisant à une décroissance de la luminescence donnée par :

où Η (λ ) représente la distribution dépendante de la fréquence des taux de décroissance. L'équation 14 se réduit à l'équation. 2 si Η (λ ) est égal à la fonction delta de Dirac δ (λ − λ ₀ ), ou il peut représenter une série continue d'exponentielles pondérées par la distribution sélectionnée. Une fonction lognormale semble un choix raisonnable dans les systèmes de nanocristaux puisque de nombreux ensembles de nanocristaux suivent naturellement des distributions de taille lognormales [22]. Afin d'éviter toute confusion supplémentaire, nous utilisons la définition normalisée standard de la fonction lognormale donnée par :

de sorte que la fonction de décroissance mesurée est

Comme pour la fonction SE, il n'y a que deux variables indépendantes (ainsi qu'un décalage et un facteur d'échelle). Les moments sont définis comme d'habitude; c'est-à-dire que le taux médian est donné par exp (μ ), la moyenne par exp (μ + σ ² /2), et la durée de vie la plus probable (le pic de la distribution) est exp (μ − σ ² ). Auparavant, une distribution non standard était utilisée [16] (c'est-à-dire une distribution qui, bien que valable en soi, n'est pas la fonction de distribution lognormale communément acceptée). L'équation 14 s'applique également à une distribution de désintégration radiative (c'est-à-dire AQY = 100%). En fait, il a été suggéré que les distributions de taux de décroissance sont pondérées par une fonction d'efficacité quantique (inconnue) [16]. Dans des situations réelles, il faut simplement accepter cette mise en garde étant donné qu'il est difficile voire impossible de connaître la distribution de la population des taux non radiatifs dans l'échantillon.

Les désintégrations de la luminescence peuvent également correspondre à une réaction de second ordre (c'est-à-dire la désintégration « bimoléculaire ») [23]. Ici, la vitesse à laquelle la population décroît est donnée par dc /dt = − λ [c _t ] ² , ce qui donne une fraction restante c _t /c ₀ = (c ₀ λt + 1) ⁻¹ . L'insertion de cette expression dans l'Eq. 1 entraîne une décroissance en loi de puissance :

Le modèle bimoléculaire n'a qu'une constante de vitesse λ (contrairement à l'exponentielle étirée et à la lognormale, qui ont des distributions de taux), et il n'y a pas de durée de vie moyenne. Plus précisément, l'intégrale temporelle diverge et la durée de vie moyenne de la désintégration du second ordre est infinie.

La fonction SE « standard » (Eq. 9) a été de loin le modèle dominant utilisé pour les décroissances de luminescence SiNC, avec de nombreux articles consacrés à l'interprétation de la signification de la décroissance pour les mécanismes de luminescence. La distribution de durée de vie lognormale a été appliquée pour la première fois aux SiNCs assez récemment [17, 24, 25]. De toute évidence, il y a peu de raisons a priori de supposer un modèle, et il serait plutôt préférable d'établir directement la distribution des taux de décroissance. Ceci peut, en principe au moins, être réalisé par la spectroscopie à résolution de fréquence en quadrature (QFRS), qui a été appliquée à plusieurs reprises au silicium amorphe mais pas aux SiNC.

Spectroscopie à résolution de fréquence en quadrature

La méthode QFRS est assez peu rapportée dans la littérature, principalement limitée à quelques études de verres dopés aux terres rares [26,27, et a-SiOx:H. Mater Sci Eng B 105:165–168" href="/articles/10.1186/s11671-018-2785-x#ref-CR28" id="ref-link-section-d291096563e3613">28] et du silicium amorphe [29, 30, 31]. La base de la technique est d'exciter l'échantillon avec un faisceau de pompe modulé en onde sinusoïdale de fréquence angulaire ω et pour mesurer la phase et l'amplitude de la luminescence lorsqu'elle tente de suivre l'excitation. Avec cette configuration, la composante en quadrature (Q ) d'un détecteur sensible à la phase (c'est-à-dire un amplificateur à verrouillage) fournit une mesure directe de la distribution de la durée de vie [30]. Étant donné que l'amplitude de l'oscillation laser modulée par l'AOM peut dépendre de la fréquence, la composante en quadrature du PL, Q _PL = Z _PL péché (Δθ _PL ) doit être normalisé à l'amplitude de l'oscillation laser, Z _LA .

Le signal FRS en quadrature est compliqué par le fait qu'une seule décroissance exponentielle n'entraîne pas de fonction delta dans le spectre QFRS. Le signal observé est en fait la convolution de la distribution de durée de vie avec une seule fonction de réponse exponentielle donnée sur une échelle logarithmique par [31].

Où la constante de temps τ ₀ = ω ₀ ⁻¹ . Ainsi, à moins que la distribution du taux de décroissance ne s'étende sur plusieurs décennies, une déconvolution doit être effectuée afin d'extraire une distribution significative.

Résultats et discussion

Caractérisation de base

En raison du faible contraste associé aux SiNC et du contraste marbré chevauchant du support de carbone amorphe, les algorithmes de comptage de particules informatisés utilisant des images en fond clair ne peuvent pas être appliqués et les diamètres ont dû être estimés « à l'œil » à l'aide d'un logiciel de comptage de pixels ( des échantillons d'images MET à fond clair sont montrés sur la Fig. 2a, d et les résultats du comptage manuel des particules ont été ajustés avec une distribution lognormale (Fig. 2c, f) afin d'obtenir un diamètre moyen linéaire de 2,9 nm (moyenne et écart type de les logarithmes naturels μ = 1.057 et σ = 0.1555) et 5.4 nm (μ = 1.663 et σ = 0.1917), pour des températures de recuit de 1100 et 1200 °C, respectivement. Ces échantillons seront dorénavant appelés « petits » et « grands » SiNC. Les tailles ont été en outre vérifiées par imagerie à haute résolution de NC sélectionnées (Fig. 2b, e), où les franges du réseau pourraient être utilisées comme un autre moyen d'identifier les NC et d'estimer leurs diamètres. La spectroscopie infrarouge à transformée de Fourier (FTIR) et les données XPS ont montré que les SiNC préparés ont été fonctionnalisés avec succès avec du dodécène ; cependant, les petits SiNC sont plus oxydés que les grands et présentent donc un degré de fonctionnalisation plus faible (Fichier supplémentaire 1 :Figures S1 et S2).

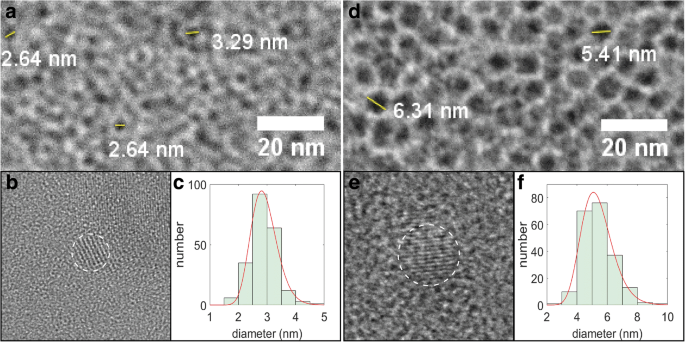
Images MET de SiNC. un Fond clair, b haute résolution, et c histogramme de distribution de taille pour les petits SiNC. Panneaux d –f représentent un ensemble similaire d'images des grands SiNCs

Photoluminescence et spectroscopie résolue en temps

Les spectres de photoluminescence (PL) étaient centrés à 660 et 825 nm avec un maximum de pleine largeur à mi-hauteur de 123 et 198 nm pour les petites et grandes SiNC, respectivement (fig. 3 encarts). Les énergies de bande interdite indirecte sont estimées à 1,87 et 1,37 eV selon \( {E}_g\kern0.5em =\kern0.5em \sqrt{E_{g,\mathrm{bulk}}^2\kern0.5em +\ kern0.5em D/{R}^2} \) [32] avec D = 4,8 eV ² /nm ² et R étant le rayon NC, ce qui est en accord étroit pour les petites particules mais prédit une bande interdite légèrement plus petite que celle obtenue par le pic PL pour les grandes. L'AQY était de 12 % pour le petit échantillon de SiNC et de 56 % pour les grands NC. Des mesures indépendantes sur un système différent ont donné 18 % et 48 % pour les deux échantillons, ce qui est typique des incertitudes des mesures AQY [33] pour les différentes longueurs d'onde d'excitation et de coupure. Nous émettons l'hypothèse que les surfaces moins incurvées et à plus faible énergie des plus grandes NC conduisent à une meilleure fonctionnalisation de surface et à une plus petite contribution des états de surface non radiatifs au spectre PL global.

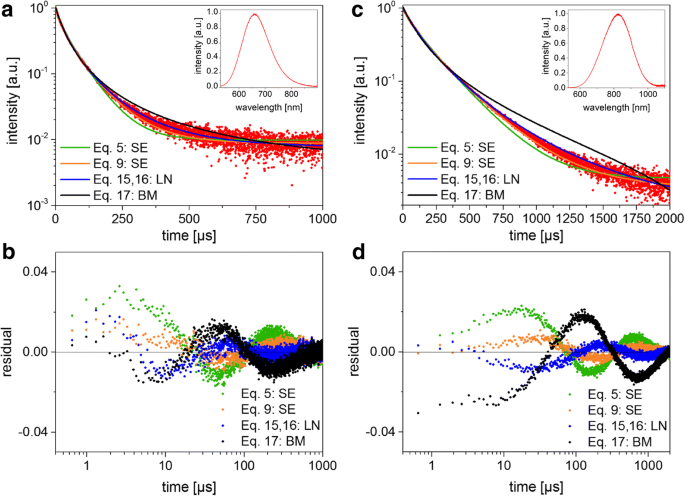
Données TRS et résultats d'ajustement. un La luminescence décline et la fonction d'ajustement correspondante (BM bimoléculaire, SE exponentielle étirée, LN lognormal) pour les petits SiNC. Le spectre PL est montré dans l'encart. b Tracés des résidus pour les ajustements (a , c , d ) montrent les courbes et les résidus pour les grands SiNC.

Les deux échantillons ont donné une décroissance non exponentielle, comme prévu sur la base de la vaste littérature précédente sur les SiNC. Les désintégrations PL mesurées ont été ajustées avec les équations. 5, 9, 16 et 17 afin de tester les différents modèles en utilisant la minimisation standard de la somme des carrés (Fig. 3). Le fait que la sensibilité du détecteur n'est pas constante sur le large spectre de luminescence NC sera discuté plus tard. Pour tous les cas, les résidus oscillent, indiquant qu'aucun des modèles ne semble totalement adéquat, mais le modèle SE « simple » (Eq. 9) et le lognormal (Eq. 16) tendent vers la somme des carrés des résidus la plus basse. Les paramètres d'ajustement calculés et les durées de vie moyennes pour les deux échantillons de SiNC sont présentés dans le tableau 2, dans lequel les moyennes dépendent clairement de la sélection du modèle de décroissance. La méthode de Higashi-Kastner a également été appliquée (Fig. 4) et les positions des pics déterminées en ajustant les courbes de temps de retard avec une gaussienne asymétrique. La méthode Higashi-Kastner donne une constante de temps t _d assez similaire à (1 /β ) ^{1 /β} ∙τ _SE , avec ces valeurs prendre de l'Eq. 9 comme indiqué avant [20]. Le modèle bimoléculaire s'adapte assez mal, cohérent avec des nanocristaux isolés qui ne sont pas fortement surexcités. Il ne sera donc pas discuté davantage.

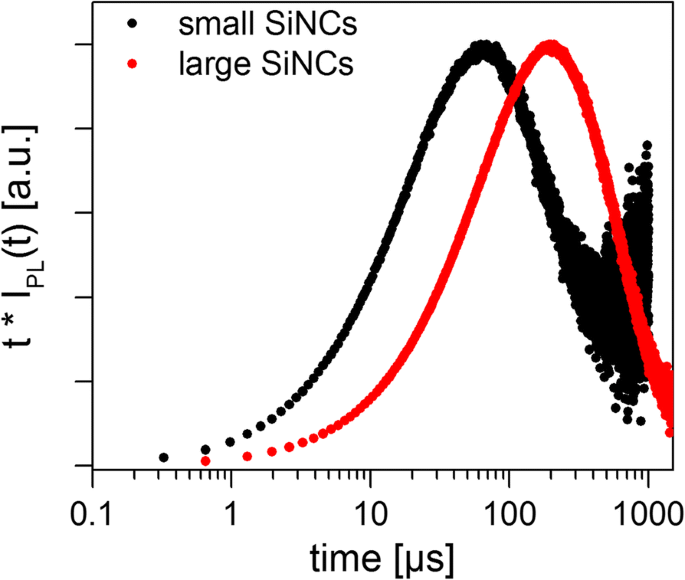
Courbes de décroissance PL normalisées multipliées par le temps de décroissance (traces de Higashi-Kastner) pour les petits et grands ensembles SiNC. Les positions de pic représentent le temps de décroissance le plus dominant, représenté par t _d dans le tableau 2

Afin d'estimer le nombre d'excitons par NC en moyenne pour ces conditions de mesure, le taux d'excitation doit être calculé à partir des sections efficaces d'absorption, qui peuvent évidemment atteindre 10 ⁻¹⁴ cm ² pour ces expériences [34]. Pour un éclairement énergétique d'excitation de 4500 W/m ² à 352 nm et aux taux d'émission de crête mesurés (voir les sections suivantes), le nombre d'excitations par NC pour les grands et les petits SiNC a été estimé à moins de ~ 1 et 0,2, respectivement. Cela suggère que les grands SiNC peuvent être légèrement surexcités. Cela peut provoquer des effets non radiatifs supplémentaires en raison de la présence de multi-excitons dans certaines NC. Afin d'évaluer davantage cette possibilité, la durée de vie a été mesurée en fonction de la puissance d'excitation; jusqu'à 2 % des valeurs indiquées ci-dessus. Les résultats n'ont montré aucune tendance et étaient toujours les mêmes à environ ~ 2% (Fichier supplémentaire 1 Figure S3), ce qui est proche des erreurs d'ajustement et de répétabilité malgré le faible rapport signal/bruit dans les mesures à faible puissance. Ainsi, l'éventuelle surexcitation des NC semble avoir peu d'effet sur les résultats.

Afin d'estimer la distribution de durée de vie à partir du TRS, les désintégrations ont été mesurées sur un ensemble de longueurs d'onde fixes à l'aide d'un monochromateur avec une bande passante de ~ 3 nm (Fig. 5). En raison de la faible intensité, un système PMT à comptage de photons a été utilisé à cette fin. Avec un rayonnement effectivement monochromatique, il ne devrait pas y avoir de différence dans les constantes de décroissance mesurées avec différents détecteurs car il y a une distribution négligeable de la fonction de réponse sur une plage de longueurs d'onde aussi étroite. La même tendance a été trouvée pour les particules à terminaison dodécyl comme observée dans d'autres NC de silicium [25, 35, 36] ; c'est-à-dire que le paramètre de dispersion augmente plus près de l'unité et que la durée de vie augmente rapidement en fonction de la longueur d'onde (Fig. 5, Tableau 3).

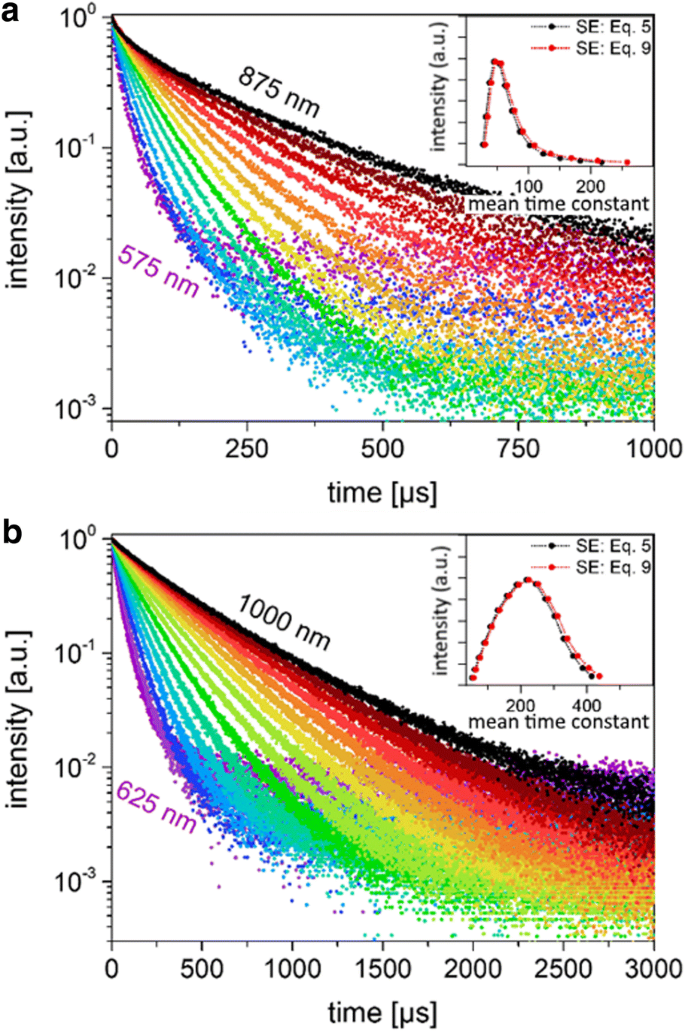
La PL à longueur d'onde étroite se désintègre. un La luminescence diminue pour les petits SiNC à des longueurs d'onde d'émission spécifiques (3 nm FWHM) allant de 575 à 875 nm, à des intervalles de 25 nm. Les données ont été ajustées avec les équations. 5 et 9, ce qui a donné un ajustement exponentiel presque unique. b La luminescence décroît à des longueurs d'onde d'émission spécifiques allant de 625 à 1000 nm pour les grands SiNC mesurés et installés dans les mêmes conditions. Les constantes de temps résultantes pour les petits et les grands SiNC sont données dans le tableau 1

Les plus petites particules ont toujours une durée de vie plus courte que les plus grosses à la même longueur d'onde de mesure. Cette observation est cohérente avec l'AQY inférieur des particules plus petites, indiquant que la durée de vie des grandes NC est moins fortement régie par des processus non radiatifs. Les grands NC sont également moins oxydés par rapport au petit échantillon NC (Fichier supplémentaire 1 Figure S1). Ainsi, alors que l'observation de l'AQY inférieur sur le petit échantillon est cohérente avec les durées de vie plus courtes mesurées, on ne peut pas faire une comparaison relative des deux échantillons via la sélection de longueur d'onde (essentiellement, la longueur d'onde d'émission dépend de la taille et le degré d'oxydation [24], qui est différent dans les deux échantillons).

Les distributions obtenues en traçant les durées de vie moyennes obtenues à partir des données monochromatiques, à l'aide des équations, sont également représentées sous forme d'encarts sur la figure 5. 5 ou 9 pour ajuster les données, en fonction de l'intensité PL à cette longueur d'onde. Comme pour ces désintégrations le paramètre bêta est raisonnablement proche de 1, il y a assez peu de différence entre les durées de vie moyennes calculées avec les deux versions du modèle SE et les distributions obtenues de cette manière semblent similaires. Bien que ces désintégrations ne représentent pas la « vraie » distribution des durées de vie en raison des contributions non radiatives à I _PL , ils peuvent néanmoins donner une indication de la distribution à vie. Pour les petites particules, on observe un pic à ~ 47 s, alors que pour les grosses NCs le pic est plus symétrique et centré autour de 220 s.

Spectroscopie à résolution de fréquence

Nous avons commencé par valider les données FRS à partir de deux standards de test :le premier était un circuit RC et le second était un échantillon de microsphères fluorescentes dopées au chélate d'Eu (Fisher Scientific). Le circuit RC a une décroissance mono-exponentielle dans laquelle les données FRS correspondent à l'Eq. 9 d'assez près et a culminé à 12,7 kHz, en accord avec la constante de temps de décroissance mesurée de 78,9 s. Le spectre Eu-chélate PL a culminé à 650 nm avec un temps de décroissance de l'ordre de centaines de microsecondes, présentant un standard pour les Si NC. La luminescence a également diminué de manière presque mono-exponentielle avec une durée de vie de 670 s. Les données FRS étaient centrées à ~ 1570 Hz avec une largeur pratiquement égale à la fonction de réponse (Eq. 18), ce qui est assez proche du résultat TRS observé. La différence (636 contre 670 s) pourrait être due au comportement légèrement non exponentiel de la décroissance couplée à la méthode d'excitation, comme expliqué plus loin.

Les données FRS pour les Si-NC sont problématiques car les résultats QFRS observés se sont avérés être à peine plus larges que la fonction de réponse (voir l'encadré de la figure 6a). Par conséquent, une déconvolution doit être effectuée sur les données, qui doivent être presque exemptes de bruit afin d'éviter des problèmes importants avec la procédure de déconvolution. We used the Richardson-Lucy deconvolution method [37] in order to enforce a positivity constraint. The deconvolved and normalized QFRS data then yield the measured lifetime distribution directly, as shown in Fig. 6 for the large and small NCs, respectively (red points), without assuming any model a priori. For both samples, we find a broad lifetime distribution that, in the case of the large NCs, is slightly skewed toward higher frequencies, whereas the small NCs distribution is more nearly symmetrical on a semilog plot. The decay rate distribution peaked at 19,900 Hz (50.3 μs) for the small NCs, whereas for the larger NCs the distribution peaked at 6280 Hz (159.2 μs).

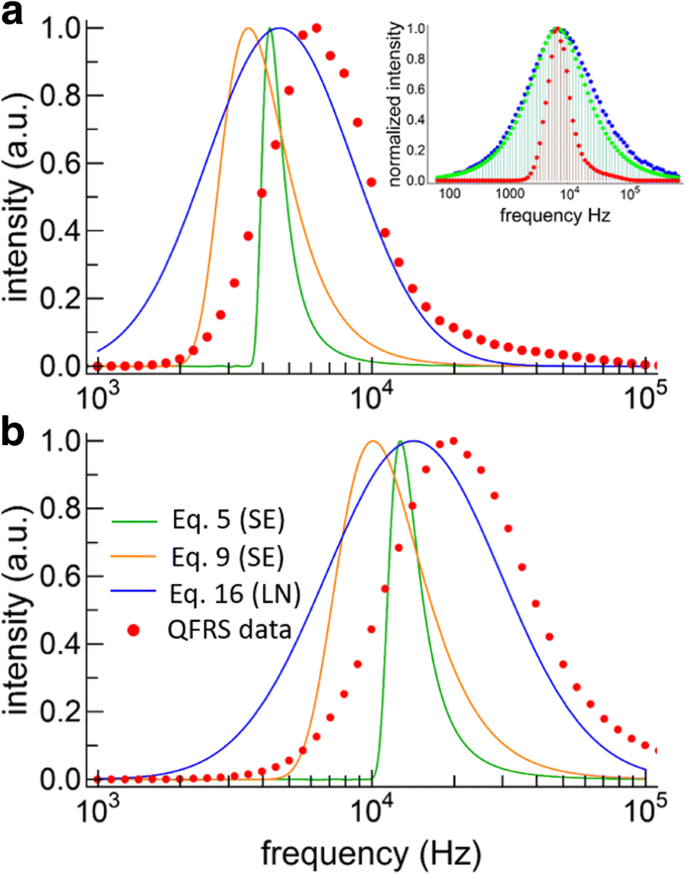
Lifetime distributions. un Lifetime distributions for large SiNCs obtained from fitting the TRS data with the two SE models and the LN model. The deconvolved QFRS data is also shown (red points). The inset shows the raw QFRS data for this sample (blue), the response function (green), and the deconvolution (red). b Lifetime distributions obtained by model fitting the TRS data (lines, same color scheme for both graphs) and QFRS (red points) for the small SiNCs

The lifetime distributions obtained from the stretched exponentials (orange and green curves) and lognormal (blue curve) model fits are also plotted in Fig. 6 for the large and small particles. The three decay models yield different distributions, both in terms of the overall shape and the peak frequencies. For both samples, the QFRS peaks at a higher frequency than any of the TRS model fits. While this may seem surprising, the same effects have been observed for CdSe NCs having a distribution of lifetimes [38, 39]. In fact, the TRS decay curve for CdSe NCs was evidently sensitive to the pulse duration, with shorter pulses accentuating the shorter lifetimes and the opposite case for long pulses. Furthermore, the mean lifetimes obtained by long-pulse duration techniques were a factor of 3–4 times longer than those obtained by phase measurement, which was due to preferential excitation of the long-lived population in steady-state excitation [38]. Indeed, the response function for TRS with a slow repetition rate is narrower than for FRS, cutting off especially sharply on the high frequency side [29]. Essentially, FRS accentuates the short-lived components of the ensemble decay more than steady-state TRS does, and this may account for the difference in the peak frequencies obtained by TRS model fitting and FRS. Despite these inherent differences, FRS appears suited to uncovering the distribution of lifetimes in ensembles of SiNCs, because it is obtained by direct measurement rather than by an assumed model. For SiNCs typical of a thermally grown ensemble, the main drawback of FRS is the necessity of a deconvolution.

While the detector response function certainly affects the QFRS, it plays a role in the TRS data as well. Indeed, measuring the ensemble decay with the APD vs. the PMT setup yielded mean decay times that were different by a factor of ~ 2, regardless of the fitting model applied. The detector responsivity also affects choice of the TRS “best” model fit. As mentioned above, our Thorlabs APD responsivity peaks at 600 nm, whereas for our Hamamatsu PMT the responsivity maximizes at 850 nm, in the long-wavelength, slow-decay part of the SiNC spectrum. Although apparently not reported before in the literature on SiNCs, this issue means that wide-spectrum TRS results from different setups are not comparable. Unfortunately, despite some critical conclusions, ref. [38] also used different detectors to compare the decay dynamics from the same wide-band NC sample and the response functions may not have been the same. Fortunately, however, the phase measurements and the steady-state measurements used the same detector (as was the case here) and the differences in the observed dynamics for these situations remain valid. Finally, the detector response function is in principle correctable in the FRS data if the responsivity curve and monochromated decay rate distribution are known over a wide range of wavelengths (i.e., decay rates). The responsivity correction has no such simple solution with TRS alone.

Conclusions

The most common models used for SiNC luminescence decay were described theoretically. The population decay corresponding to the “simple” stretched exponential luminescence decay, exp[− (t /τ ) ^β ], was derived and expressions for the characteristic mean times were found. This model was compared against the alternative model in which the population decays according to the simple SE. Two dodecene-functionalized SiNCs samples were then prepared from thermal nucleation and growth, followed by etching and alkane surface functionalization. These samples consisted of particles with mean diameters of 2.9 and 5.4 nm, respectively. The basic PL spectrum and TRS was measured using standard methods. The TRS data were fit with several distributions in order to establish whether any of them can be considered “true” and to find which one yields the best fit. While the simple SE luminescence decay fits the TRS data reasonably well, the distribution of residuals shows that it is not strictly accurate. None of the fitting models fully captures the shape of the measured decay rate distribution; they also show large deviations in the peak position and the shape of the distribution, as well as disagreement in the average time constants. Furthermore, the ensemble mean time constants were dependent on the responsivity curve of the detection system. This leads to serious questions about how to interpret the PL decay from ensembles of thermally-grown SiNCs.

Quadrature frequency-resolved spectroscopy was then employed with the intent to find the lifetime distribution directly for SiNC ensembles formed by thermal annealing of a base oxide. The spectrum was found to be not much wider than the intrinsic QFRS response function, requiring a deconvolution in order to extract the SiNC rate distribution. This yielded a distribution whose shape was nearly symmetrical (on a semilog scale) for the small NC sample and about half a decade wide, whereas it was slightly more skewed for the large NCs. We find that FRS techniques are suited to the study of SiNC luminescence dynamics and, after deconvolving the system response from the data, FRS yields the decay rate distribution directly. The most significant problem is the required deconvolution, but the Richardson-Lucy method was found to produce fairly robust results. While the detector response function can in principle be corrected from the FRS data, there is no simple means to do this for wide-PL-band TRS data. Still, as long as the data compared are from the same detector then the results should at least be internally meaningful. Hopefully in the future, these issues will be more fully considered when analyzing inhomogeneously broadened NC luminescence lifetimes, rather than defaulting to the simple stretched exponential model (Eq. 9) to describe and characterize the dynamical processes at work in the PL spectrum.

Methods

The SiNCs were synthesized according to a recently-proposed method [21]. Briefly, 4 g of hydrogen silsesquioxane (HSQ) was annealed at 1100 or 1200 °C for 1 h in a flowing 5% H₂  + 95% Ar atmosphere, resulting in composites of SiNCs embedded in a silica matrix. These composites were mechanically ground into a fine powder using an agate mortar. The powder was shaken for about 8 h with glass beads using a wrist action shaker. The powders were suspended in 95% ethanol and interfaced to a vacuum filtration system equipped with a filter. To liberate the H-SiNCs, the silica matrix was removed via HF etching. An approximately 200 mg aliquot of the composite was transferred to a Teflon beaker to which 2 mL of ethanol, 2 mL of water, and 2 mL of 49% HF aqueous solution were added in order to dissolve the silica matrix. After stirring the suspension for 40 min, the liberated H-SiNCs were extracted as a cloudy yellow suspension using toluene and isolated by centrifugation at 3000 rpm for 5 min. The resulting hydrogen-terminated SiNCs were suspended in 10 mL dry toluene, and then transferred to an oven-dried Schlenk flask equipped with a magnetic stir bar. Subsequently, 1 mL of 1-dodecene (ca. 4.6 mmol), as well as 20 mg of AIBN were added. The suspension was subjected to three freeze-pump-thaw cycles using an Ar charged Schlenk line. After warming the suspension to room temperature, it was stirred for 24 h at 70 °C, and 10 mL of methanol and 20 mL of ethanol were subsequently added to the transparent reaction mixture. The resulting cloudy suspension was transferred to a 50 mL PTFE vial and the SiNCs were isolated by centrifugation at 12,000 rpm for 20 min. The SiNCs were re-dispersed in 10 mL toluene and isolated by addition of 30 mL ethanol antisolvent followed by another centrifugation. The latter procedure was carried out one more time. Finally, the dodecyl-SiNCs were re-dispersed in 5 mL dry toluene and stored in a screw capped vial (concentration ~ 0.5 mg/mL) for optical studies.

TEM samples were prepared by depositing the freestanding nanoparticles directly onto an ultrathin (ca. 3 nm) carbon-coated copper TEM grid. The NCs were imaged by bright-field TEM using a JEOL JEM-2010 and HRTEM was done on a JEOL JEM-ARM200CF. Fourier transform infrared spectroscopy (FTIR) was performed in a Nicolet 8700 from Thermo Scientific. X-ray photo-electron spectroscopy was measured in a SPECS system equipped with a Phoibos 150 2D CCD hemispherical analyzer and a Focus 500 monochromator. The detector angle was set perpendicular to the surface and the X-ray source was the Mg Kα line.

Luminescence spectra were excited with a 352-nm Ar ⁺ ion laser, which was pulsed (50% duty cycle, 50–250 Hz) using an Isomet IMDD-T110 L-1.5 acousto-optic modulator (AOM) with a fall time of ~ 50 ns. The used setup is schematically depicted in Fig. 7. The laser beam passes the acousto-optic modulator and one of the diffracted beams is selected by an iris. A beamsplitter reflects the main part of the pulsed laser beam into the sample cuvette and the incident power on the sample was ~ 8 mW spread over an area of ~ 4 mm ² . The luminescence was collected with an optical fiber (numerical aperture 0.22), sent through a 450-nm longpass filter and is guided to the appropriate detector. The PL spectrum was measured by an Ocean Optics miniature spectrometer whose response function was corrected using a calibrated radiation source (the HL-3 + -CAL from Ocean Optics). The quantum efficiency was measured using an integrating sphere with 405-nm excitation, using a solution diluted to have an absorbance of ~ 0.15 at that wavelength.

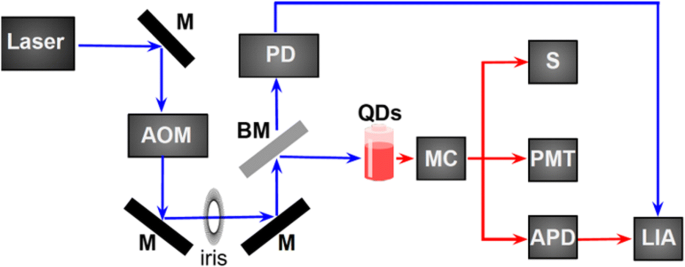
Diagram of the experimental setup. M mirror, AOM acousto-optic modulator, BM beamsplitter, PD photodiode, MC monochromator, S spectrometer, PMT photomultiplier tube, APD avalanche photodiode, LIA lock-in amplifier

The luminescence dynamics were measured with two different detectors. The first detector was the Thorlabs 120A2 avalanche photodiode (50 MHz roll-off), which was interfaced to a Moku:Lab (200 MHz) in digital oscilloscope mode. The second detector was a Hamamatsu h7422-50 photomultiplier tube interfaced to a Becker-Hickl PMS400 multiscalar. The error in the luminescence decay times was obtained by repeating the measurements three times, yielding a standard error in the mean lifetime calculated using the stretched exponential fit (Eq. 4) of 1 μs. All fits to the decay data were done in Origin using the least linear squares with the Levenberg-Marquardt algorithm, and were repeated in Matlab using the same method. For wavelength-dependent decay measurements, the luminescence was sent through an Acton MS2500i monochromator prior to detection, with the half width of the detected radiation set to ~ 3 nm.

For QFRS measurements, the AOM was set to produce a sinusoidal oscillation. A part of the incident beam was deflected into a Thorlabs PDA10A photodiode (200 MHz) in order to generate the reference signal. The SiNC PL response was simultaneously collected and sent to the APD. The reference signal was obtained using the beamsplitter, and along with the corresponding PL signal, was analyzed using the Moku:Lab in the lock-in amplifier mode to measure the in-phase and quadrature components of the signal.

Finally, we also searched for a short-lifetime component in the luminescence, as has sometimes been reported previously and attributed to oxidation [22]. This system used a 405-nm picosecond diode laser (Alphalas GmbH) to excite the NCs, and a Becker-Hickl HPM-100-50 PMT interfaced to an SPC-130 pulse counter system. This setup has a response time of ~ 100 ps. No evidence of a nanosecond decay was observed in these SiNCs.

Abréviations

APD:

Avalanche photodiode

AQY:

Absolute quantum yield

FRS:

Frequency-resolved spectroscopy

LN:

Lognormal

NCs:

Nanocrystals

PL:

Photoluminescence

PMT:

Photomultiplier tube

QFRS:

Quadrature frequency-resolved spectroscopy

SE:

Stretched exponential

SiNCs:

Silicon nanocrystals

TRS:

Time-resolved spectroscopy