Diffusion aux petits angles à partir de fractales de graisse à l'échelle nanométrique

Introduction

De nombreuses structures hiérarchiques générées à l'échelle nano et micro ont des caractéristiques géométriques invariantes sous des dilatations d'échelle, affichant une auto-similarité, et portant ainsi des propriétés fractales [1, 2]. Bien que les progrès récents de la science des matériaux et de la nanotechnologie permettent la préparation de diverses fractales déterministes artificielles à l'échelle nano/micro, avec une auto-similitude exacte [3-7], la grande majorité des processus naturels génèrent des fractales aléatoires et statistiquement auto-similaires. Une bonne approximation dans les études structurales des formations fractales naturelles peut se faire en recourant à des modèles fractals déterministes, avec la même dimension fractale que les modèles aléatoires. Cette approche a été utilisée avec succès pour montrer que le transfert à travers des surfaces fractales aléatoires est très proche de la réponse des géométries de modèles déterministes [8]. En introduisant la polydispersité dans l'algorithme de construction d'une fractale déterministe, des intensités de diffusion aux petits angles (SAS) similaires à celles correspondant aux fractales aléatoires peuvent être obtenues [9]. De plus, une approche « déterministe » est plus efficace sur le plan informatique, permettant une description analytique de diverses propriétés, telles que la forme fractale, les facteurs de structure et le rayon de giration.

L'une des méthodes les plus fiables pour déterminer les propriétés structurelles des fractales déterministes et aléatoires [10, 11] utilise la diffraction des ondes dans le contexte de la diffusion aux petits angles sur des matériaux nano- ou micro-structurés, en utilisant des neutrons ou des ondes électromagnétiques (x -rayon, lumière, etc.) [12]. C'est pourquoi, l'une des tâches fondamentales des descriptions théoriques liées aux déterminations expérimentales dans ce domaine de recherche est de révéler la relation entre la structure des fractales et leur spectre de diffraction correspondant ou la distribution d'intensité de diffusion en fonction du vecteur d'onde de diffusion. De nombreuses études expérimentales et théoriques ont été menées dans ce sens [13-21].

À l'aide de calculs théoriques standard et d'interpolation, le paramètre qui est déterminé à partir de ce type de mesures expérimentales est la dimension fractale de masse D _m (voir Annexe 1), avec D _m D _s , avec d -1<D _s <d . Nous avons noté d la dimension euclidienne dans laquelle la fractale est noyée. La dimension fractale de la masse décrit la manière dont la masse M (r ) varie lorsqu'il est noyé dans un disque de rayon r . Le masse-rayon obtenu la relation \(M(r) \propto r^{D_{\mathrm {m}}}\) conduit au comportement de l'intensité de diffusion \(I(q) \propto q^{-D_{\mathrm {m} }}\). Évidemment, D _m peut être identifié avec l'exposant de la dépendance de la loi de puissance de l'intensité de diffusion en fonction du vecteur d'onde de diffusion q [18, 22]. Plus la valeur de D est élevée _m , plus la structure est compacte. De même, dans le cas d'une fractale surfacique, sa distribution surfacique obéit à \(S(r) \propto r^{2-D_{\mathrm {s}}}\), et donc, \(\phantom {\dot { i}\!}I(q) \propto q^{-(2\mathrm {d}-D_{\mathrm {s}})}\) [19, 23]. Travailler dans l'espace euclidien tridimensionnel, D _s approche le minimum de deux, lorsque la surface est presque parfaitement lisse. Il tend vers le maximum de trois, s'il est tellement plié qu'il remplit presque complètement l'espace.

De nombreuses intensités de diffraction expérimentales provenant de divers systèmes synthétisés chimiquement et biologiques sont caractérisées, sur une double échelle logarithmique, par une succession de désintégrations en loi de puissance, entrelacées par des régions d'intensité constante. Ce comportement peut être identifié pour certains gels polymères [24], glycoside hydrolase pour substrat cellobiose [25], coacervats complexes polyélectrolytiques [26] ou carbone nanoporeux [27]. Bien que le modèle classique de Beaucage [28] puisse fournir des informations structurelles de base sur ces systèmes (c'est-à-dire la dimension fractale de masse ou de surface et la taille globale de chaque niveau structurel), une caractérisation plus complète est nécessaire en raison du grand nombre de configurations une valeur fixe de la dimension fractale. Ce problème a été récemment partiellement traité par Cherny et al. [29] dans le cadre des modèles de diffusion aux petits angles (SAS). Il a été montré que, pour les fractales de masse déterministes à une seule échelle, des informations supplémentaires peuvent être obtenues, telles que le nombre d'itérations fractales, le nombre d'unités constituantes de base et le facteur d'échelle. Cette approche a en outre été utilisée avec succès pour développer de nouveaux modèles pour les fractales grasses, si des successions de désintégrations de loi de puissance sont présentes dans les distributions de diffusion. Il peut être appliqué aux structures où la taille globale des unités de base constitutives est du même ordre que les distances entre elles [30, 31].

Le modèle théorique présenté dans cet article combine des modèles antérieurs pour étendre leur applicabilité. Il décrit des successions de désintégrations en loi de puissance, avec des valeurs arbitrairement décroissantes des exposants de diffusion, et entrelacées par des régions d'intensité constante. Notre modèle est également capable de fournir des informations plus détaillées sur chaque niveau structurel dans la nano-/micro-fractale. Pour cela, nous considérons une fractale grasse, représentée par une fractale de masse déterministe à deux dimensions avec un facteur d'échelle dépendant du nombre d'itérations, mais avec une surface non nulle dans la limite d'un grand nombre d'itérations, donc avec un Mesure de Lebesgue. Nous dérivons des expressions analytiques des facteurs de forme et de structure fractales, et nous montrons comment déterminer les dimensions fractales et les facteurs d'échelle à chaque niveau structurel.

Contexte théorique

Considérant un réseau d'ouvertures de diffraction identiques orientées de manière similaire, désigné ici par Σ , contenant N régions transparentes, étiquetées par j , une sommation des amplitudes obtenues à partir de chaque ouverture doit être prise en compte. Ainsi, la distribution de fréquence bien connue de l'amplitude de diffraction d'une seule ouverture (Eq. (37) en Annexe 2) peut être réécrite comme [32] :

Les coordonnées d'un point dans le repère local du j ème ouverture sont (x _j ,y _j ), et T (x,y ) représente la fonction de transmission individuelle correspondant à chaque région transparente. On peut échanger la sommation avec l'intégration car, dans notre cas, les ouvertures sont décrites par la même fonction de distribution individuelle, de sorte que l'Eq. (1) peut être réécrit comme :

Le facteur intégral de l'égalité précédente représente la transformée de Fourier de la fonction de distribution de chacune des ouvertures identiques, comme indiqué ci-dessus. Cette amplitude est modulée par le facteur contenant la sommation, représentant la transformée de Fourier des distributions Dirac-delta de la forme \(A_{\delta }~=~\sum _{j~=~1}^{N}(x~ -~x_{j})(y~-~y_{j})\). Par conséquent, la distribution spatiale des ouvertures à l'intérieur du réseau est également prise en compte. Ainsi, l'éq. (2) peut être réécrit sous la forme dite du théorème du tableau [32] :

La distribution d'intensité de l'image diffractée dans le plan de Fourier devient :

Comme on s'y attend, le premier facteur du produit correspond à l'intensité de diffusion d'un seul trou, tandis que le second révèle la manière dont ces trous sont répartis dans l'ouverture de diffraction Σ . Ces quantités sont également connues sous le nom de facteur de forme F (p,q ) et, respectivement, le facteur de structure S (p,q ). C'est pourquoi, les résultats obtenus tout au long de l'article seront exprimés sous la forme d'intensité de diffusion suivante :

Modèle et méthode fractales grasses

La procédure détaillée pour construire une fractale de Cantor mince (régulière) est bien connue [33]. Seule la procédure de construction principale est résumée ici. Une approche de haut en bas est adoptée. Commençant par un carré initial (ou toute autre forme euclidienne) d'arête l ₀ (à m =0), dont le centre coïncide avec l'origine du repère cartésien et les arêtes parallèles aux axes du repère, tout point du carré satisfait aux conditions −l ₀ /2≤x ≤l ₀ /2 et −l ₀ /2≤y ≤l ₀ /2. À la première itération (m =1), le carré est divisé en quatre autres carrés, de longueur d'arête \(\beta _{\mathrm {s}}^{(1)}l_{0}\). Nous avons noté \(\beta _{\mathrm {s}}^{(1)} \equiv (1-\gamma _{1})/2\), avec \(0 <\beta _{\mathrm { s}}^{(1)} <1/2\), le premier facteur d'échelle d'itération, et avec γ ₁ la fraction de la longueur enlevée à ce point, comme on peut le voir sur la Fig. 1 a, b) pour m =1. Le nombre placé entre (⋯), apparaissant comme index supérieur, quantifie le nombre d'itérations. Il ne doit pas être interprété comme un exposant d'une fonction puissance. En termes de facteur d'échelle, les positions des quatre carrés sont données par les vecteurs \(\boldsymbol {a}_{j}~=~\left \{ \pm \beta _{\mathrm {t}}^{ (1)}l_{0}, \pm \beta _{\mathrm {t}}^{(1)}l_{0}\right \}\) avec toutes les combinaisons de signes possibles, où \(\beta _{ \mathrm {t}}^{(1)}~=~\left (1-\beta _{\mathrm {s}}^{(1)}\right)/2\) est utilisé pour simplifier davantage les formulations. Le carré a été choisi comme forme initiale, en raison de la simplicité des calculs numériques. Toute autre forme géométrique, par exemple un cercle, peut être envisagée. L'effet du choix d'une autre forme n'est observé que dans la région de Porod du facteur de forme, ce qui dépasse le cadre de cet article.

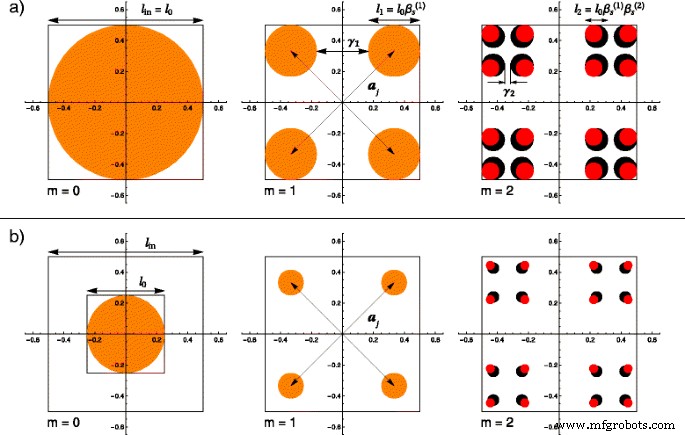
(Couleur en ligne) Une comparaison entre les fractales régulières et grasses pour les deux premières itérations, où la forme de base à m =0 est un disque de diamètre l ₀ et la taille fractale est l _dans :a l ₀ =l _dans; b l ₀ =l _dans /f , avec f =2. Dans les deux cas, à m =1 les structures coïncident en raison de facteurs d'échelle égaux \(\beta _{\mathrm {s}}^{(1)}\). Commençant par m =2, la grosse fractale a un facteur d'échelle plus grand \(\left (\beta _{\mathrm {s}}^{(2)}> \beta _{\mathrm {s}}^{(1)}\ à droite)\), et ainsi, les disques ont un diamètre plus grand (disques noirs ) que dans le cas des fractales régulières (disques rouges ); un _j sont les vecteurs de position et γ _i sont les fractions de longueur supprimée à i ème itération

Les deux premières étapes décrites ci-dessus sont également appliquées dans la construction de la version classique d'une grosse fractale, pour les itérations m =0 et m =1. C'est pourquoi, jusqu'à présent, ces deux structures coïncident. Pour obtenir la grosse fractale, une modification de l'algorithme utilisé à l'itération m =1 doit être fait, en choisissant un autre facteur d'échelle à m =2, \(\beta _{\mathrm {s}}^{(2)} \equiv (1 - \gamma _{2})/2\). En appliquant l'ensemble de l'algorithme dans la limite d'un nombre élevé d'itérations [34, 35], on obtient à nouveau la version classique d'une grosse fractale. Il ressort clairement de la construction que la version régulière de la fractale est récupérée lorsque les facteurs d'échelle, à chaque itération, sont choisis pour être égaux \(\beta _{\mathrm {s}}^{(1)}~=~ \beta _{\mathrm {s}}^{(2)}~=~\cdots =\beta _{\mathrm {s}}^{(m)}\).

Afin d'obtenir le plateau constant entre deux décroissances en loi de puissance dans le comportement de l'intensité SAS, nous devons tenir compte du fait que les distances entre les unités de diffusion sont beaucoup plus grandes que leur taille globale. Une telle approche a d'abord été utilisée dans le cadre de modèles fractals de surface [36, 37]. Compte tenu du rapport f de la distance totale entre les unités de diffusion l _dans et leur taille globale l ₀ , on a :

Pour les expériences de diffusion affichant des plateaux d'intensité constante entre deux régions fractales, les valeurs de f ≫1 doit être choisi. Dans le cas des fractales de surface, augmenter la valeur de f conduit à un meilleur accord entre l'intensité SAS totale, d'une part, et l'approximation d'unités de diffusion indépendantes, d'autre part [36, 37].

En utilisant les considérations ci-dessus, on peut décrire les différences entre les fractales régulières et les grosses. L'influence du facteur f , introduit ci-dessus, peut également être visualisé. C'est pourquoi, sur la figure 1, nous illustrons graphiquement la comparaison à l'aide d'un disque de rayon r ₀ ≡l ₀ /2=l _dans /(2f ) comme forme de base. Les résultats des deux premières itérations, affichés dans chaque ligne de la figure 1, représentent les structures obtenues pour une fractale régulière (marquée par des disques rouges) et une fractale grasse (représentée par un disque noir), qui peuvent également être totalement superposées ( marqués comme des disques orange). Dans la ligne intitulée Fig. 1 a, le facteur f est considérée comme égale à l'unité de sorte que les constructions classiques et les formes fractales sont obtenues. La deuxième rangée de la figure, notée Fig. 1b, montre l'influence du facteur présenté ci-dessus. Dans ces calculs, nous avons choisi la valeur arbitraire de f =2. On observe qu'aux itérations m =0 et m =1, dans les deux cas a et b, les structures obtenues des ensembles de Cantor régulier et gras sont identiques et complètement superposées. Ceci est à prévoir en raison du facteur d'échelle commun. Cependant, comme on peut le voir dans la dernière paire d'images de la figure 1, commençant par m =2, les rayons des disques de la grosse fractale sont plus grands car son facteur d'échelle \(\beta _{\mathrm {s}}^{(2)}\) est plus grand, par définition, que celui de la normale. Dans la dernière image de la figure 2 b, la taille des disques est beaucoup plus petite que dans son homologue de la figure 2 a en raison de la valeur non unitaire du facteur f .

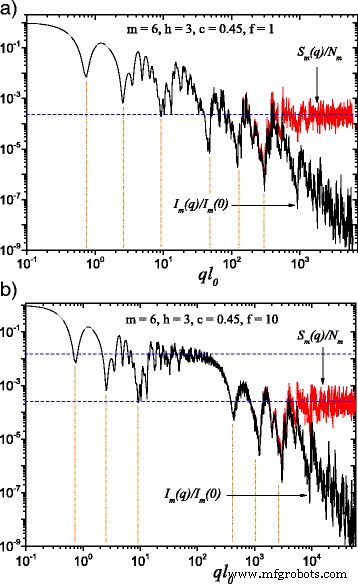
(Couleur en ligne) Une comparaison entre l'intensité de diffusion donnée par l'Eq. (22) (courbes noires ) et le facteur de structure donné par l'équation. (24) (courbes rouges ) à m =6 et moyenné sur les orientations selon l'Eq. (25). Ici, h =3 (c'est-à-dire que le facteur d'échelle est maintenu constant pendant trois itérations consécutives), tandis que la forme de base dans le calcul de l'intensité de diffusion est un carré de taille de bord l ₀ :a l ₀ =l _dans; b l ₀ =l _dans /f (avec f =10). Lorsque f ≠1, un plateau d'intensité constante apparaît entre les deux désintégrations généralisées en loi de puissance (Fig. 2 b). Lignes horizontales notons l'asymptote du facteur de structure ≃1/N _m , tandis que les positions des minima sont estimées selon l'équation. (26)

Pour obtenir les lois de puissance elles-mêmes, il faut généraliser davantage le modèle fractal classique de la graisse. Ceci est fait en considérant que les changements de facteur d'échelle ne sont pas effectués à chaque itération, mais à chaque seconde, troisième, ⋯ ou, de manière générale, chaque h ème itération. La fraction des longueurs enlevées au m l'itération est :

avec 0<c <1. La fonction p _m est défini comme :

pour toute valeur entière positive de m , avec h =1,⋯,m , où la fonction plancher ⌊⋯ ⌋ a été utilisée. Ainsi, le facteur d'échelle correspondant au m l'itération est donnée par :

Il est clair maintenant que le but de la fonction p _m est de garder le facteur d'échelle constant pour h itérations (h <m ).

Les composantes des vecteurs de position de chaque carré peuvent être écrites comme :

tandis que la longueur du bord de chaque carré est donnée par :

Le facteur f est à utiliser dans la formule de la longueur l ₀ prendre en compte que pour les itérations entre les (h +1)e et m ème, la taille des carrés diminue en fonction des distances entre eux :

où h <m . Le nombre de carrés à chaque itération est :

Ainsi, à chaque échelle, considérée comme itération à facteur d'échelle constant, on a une dimension fractale différente donnée par [29, 38, 39] :

Dans la limite d'un grand nombre d'itérations, la dimension fractale de l'ensemble fractal construit sera [34] :

qui est la valeur attendue pour une grosse fractale bidimensionnelle. Enfin, si a _i est la zone relative supprimée à i ème itération, alors \(\prod _{i=1}^{m}(1-a_{i})> 0\) si \(\sum _{i=1}^{\infty } a_{i} <\infty \), et ainsi, le modèle satisfait la définition et les caractéristiques des fractales grasses [35].

Résultats et discussion

D'après le principe de Babinet, on peut conclure qu'à m e itération, les ouvertures dans le réseau sont les carrés restants dans la fractale, tandis que les parties supprimées deviennent opaques au rayonnement.

Intensité de diffusion monodisperse et facteur de structure

Afin de dériver l'expression analytique de l'intensité de diffusion pour la fractale de Cantor gras, nous commençons par écrire la relation de récurrence de la transmittance du réseau pour une itération arbitraire correspondant à 1D Cas. À m =0, nous avons

Compte tenu de l'algorithme de construction de la fractale, la transmittance après la première itération est donnée par :

$$ \begin{aligned} T_{1}(l_{1}, x,) =T_{0}(l_{1}, x) \ast \delta\left(\frac{x-l_{0}\ beta_{\mathrm{t}}^{(1)}}{l_{1}}\right) + \\ T_{0}(l_{1}, x) \ast \delta\left(\frac{x +l_{0}\beta_{\mathrm{t}}^{(1)}}{l_{1}}\right),~~~~~~~~~~~~ \end{aligned} $$ (17)

où δ (x −un ) est la distribution Dirac-delta unidimensionnelle à x =un . Le symbole représente l'opérateur de convolution. Par conséquent, à m ème itération, on peut écrire :

$$ \begin{aligned} T_{m}(l_{m}, x) =T_{m-1}(l_{m}, x) \ast \delta\left(\frac{x-u_{m} }{l_{m}} \right) + \\ T_{m-1}(l_{m}, x, y) \ast \delta\left(\frac{x+u_{m}}{l_{m }} \right),~~~~~~~~~~~~ \end{aligned} $$ (18)

où \(u_{m}~=~l_{0}\beta _{\mathrm {t}}^{(m)}\prod _{j=1}^{m-1}\beta _{\mathrm {s}}^{(j)}\). Effectuer une transformée de Fourier sur l'équation. (18), on trouve que l'amplitude diffusée à m l'itération est :

$$ A_{m}(p)=2^{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\prod\limits_{i=1}^{ m}\cos(2\pi p u_{i}). $$ (19)

Depuis le 2D Le modèle fractal de graisse est un produit direct de deux fractales de graisse unidimensionnelles, sa transformée de Fourier peut être écrite comme le produit de deux transformées de Fourier unidimensionnelles. Par conséquent, l'amplitude de diffusion bidimensionnelle peut être écrite comme :

$$ A_{m}(p,s)\équiv A_{m}(p) A_{m}(s), $$ (20)

et ainsi,

$$ \begin{aligned} A_{m}(p, s) =N_{m}\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin (\pi s l_{m})}{\pi s l_{m}} \times \\ \prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}), \end{aligned} $$ (21)

de sorte que l'intensité de diffusion devienne :

$$ \begin{aligned} I_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin( \pi s l_{m})}{\pi s l_{m}} \right)^{2} \times \\ N_{m}^{2} \left(\prod\limits_{i=1}^ {m}\cos(2\pi p u_{i})\cos(2\pi s u_{i}) \right)^{2}. \end{aligné} $$ (22)

Le premier facteur de l'équation précédente, représentant l'intensité de diffraction due au facteur de forme, comme indiqué dans l'Eq. (5) :

$$ F_{m}(p, s) =\left(\frac{\sin(\pi p l_{m})}{\pi p l_{m}}\frac{\sin(\pi s l_{ m})}{\pi s l_{m}} \right)^{2}, $$ (23)

correspond à l'intensité de diffusion obtenue à partir d'un seul carré d'arête l _m . Le deuxième facteur, représentant l'intensité de diffraction due au facteur de structure, comme indiqué dans l'Eq. (5) :

$$ S_{m}(p, s) =N_{m}^{2}\left(\prod\limits_{i=1}^{m}\cos(2\pi p u_{i})\cos (2\pi s u_{i}) \right)^{2}, $$ (24)

décrit la façon dont les carrés sont distribués. L'intensité totale du rayonnement diffusé est le produit de F _m (p,s ) et S _m (p,s ).

La décroissance en loi de puissance de l'intensité, telle que formulée dans l'équation. (22), est obtenu après avoir effectué la moyenne sur toutes les orientations [29]. En considérant une probabilité égale pour toute orientation, la moyenne peut être calculée dans le cas de fractales à deux dimensions en intégrant sur toutes les directions du vecteur de diffusion q =(p,s ):

$$ \langle f(p, s) \rangle =\frac{1}{2\pi} \int_{0}^{2\pi}f(q,\phi)\mathrm{d}\phi, $ $ (25)

où p =q cosϕ et s =q péchéϕ . Ainsi, l'intensité de diffusion I (q ) est obtenu en fonction du module de transfert de quantité de mouvement q ≡|q |.

Car, d'après la définition du facteur de structure, on a \(S_{m}(0)~=~N_{m}^{2}\), où N _m est le nombre de carrés, tel que défini dans l'équation. (13), la procédure standard de normalisation S _m (0) =1 peut être adopté, comme décrit dans [11, 29].

Les résultats calculés pour l'intensité de diffusion monodisperse I _m (q ) et le facteur de structure S _m (q ), avec m =6, sont affichés dans la Fig. 2 pour la fractale de graisse classique (f =1 dans la Fig. 2 a) et, pour le modèle fractal étendu de graisse développé dans ce travail (f =10 sur la figure 2 b). Pour obtenir la Fig. 2b, nous avons considéré h =3 pour que le facteur d'échelle \(\beta _{\mathrm {s}}^{(1)}\) des trois premières itérations soit maintenu constant, alors il avait une autre valeur constante \(\beta _{\ mathrm {s}}^{(2)}\) pour les trois prochaines itérations. Comme prévu, dans les deux cas (pour f =1 et f =10), les différences entre l'intensité de diffusion d'une part, et le facteur de structure d'autre part, peuvent être observées lorsque \(q \gtrsim 1/l_{m}\). Dans cette région, l'intensité de diffusion a une décroissance en loi de puissance I (q )∝q ⁻³ . Le facteur de structure a une valeur asymptotique qui tend vers 1/N _m , représenté par la ligne horizontale sur la figure 2a ou la ligne horizontale inférieure sur la figure 2b [29, 33].

Une succession de deux désintégrations généralisées en loi de puissance, identifiables comme une superposition de maxima et de minima, sur une simple désintégration en loi de puissance, peut être observée sur la figure 2 a. Mais sur la figure 2b, une région d'intensité à peu près constante, dans le domaine 20≲ql ₀ ≲100, peut être clairement distingué, englobé par les deux désintégrations successives de la loi de puissance généralisée. Ceci est dû à la diminution de la taille des carrés d'un ordre de grandeur (f =10) par rapport aux distances qui les séparent. Cette région, observable autour de la ligne horizontale supérieure sur la figure 2b a l'asymptote 1/N ₃ , le même que celui du facteur de structure classique de la fractale grasse, affichant un comportement similaire au cas de ne considérer que les trois premières itérations.

De plus, on peut voir sur la figure 2 que le nombre de minima à chaque échelle coïncide avec le nombre d'itérations du facteur d'échelle constant. Ces minima se produisent lorsque le rayonnement traversant différents carrés à l'intérieur de la fractale interfère et sont en opposition de phase, et donc, les distances les plus fréquemment rencontrées entre le centre des carrés (2u _m ) sont égaux à π /q . C'est pourquoi, les positions approximatives des minima sont obtenues à partir de la relation :

$$ q_{i} \simeq \frac{\pi}{2 u_{i}},~~~~i=1, \cdots, m $$ (26)

indiqué dans la Fig. 2 par des lignes verticales. Pour les six premières itérations, on observe un assez bon accord entre les positions calculées à l'aide de l'Eq. (26), et ceux trouvés dans l'intensité de diffusion, ou facteur de structure. Cette approximation pourrait être moins précise pour les itérations plus élevées, une fois que le nombre d'itérations augmente au-dessus d'une certaine valeur car dans ces cas, de plus en plus de distances sont comparables à la plus fréquemment rencontrée. Néanmoins, cette approximation fonctionnera assez bien dans la pratique, où l'on ne peut guère s'attendre à distinguer plus de quatre ou cinq de ces minima.

Pour chaque échelle individuelle, dans une plage donnée 1/(2u _i )≲q ≲1/(2u _{i +1} ), le motif de diffraction est produit par l'interférence de seulement le i itération fractale. Ceci peut être utilisé pour montrer que, dans cet intervalle, les fonctions I _m (q )q ^D et S _m (q )q ^D sont log-périodiques [29], où D est la dimension fractale correspondant à une échelle donnée. En particulier, pour les résultats montrés dans les Fig. 2 et 3, les fonctions I _m (q )q ^−1.1 et S _m (q )q ^−1.1 sont log-périodiques avec la période \(1/\beta _{\mathrm {s}}^{(1)}\) pour les trois premières itérations, tandis que I _m (q )q ^−1.51 et S _m (q )q ^−1.51 sont log-périodiques avec \(1/\beta _{\mathrm {s}}^{(2)}\) pour le deuxième groupe de trois itérations.

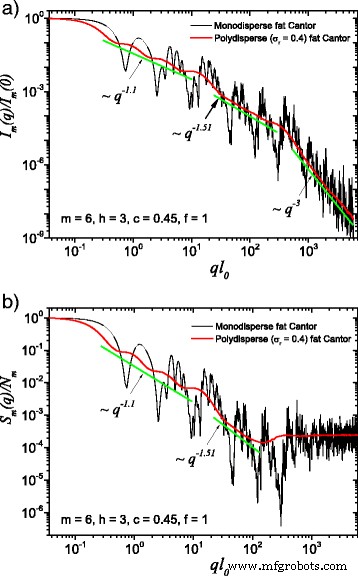
(Couleur en ligne) Une comparaison entre les systèmes monodispersés et polydispersés :a intensité de diffusion (Eq. (22)); b facteur de structure (Eq. (24)), moyenné sur toutes les orientations de la fractale, selon l'Eq. (25). Ici, f =1, m =6, h =3 (c'est-à-dire que le facteur d'échelle est maintenu constant pendant trois itérations consécutives), et la forme de base est un carré de longueur d'arête initiale l ₀ =l _dans . Dans les deux cas, la polydispersité étale les courbes de diffusion monodisperses, et les dimensions fractales peuvent être récupérées à chaque niveau structurel

De la même manière que les fractales de masse déterministes, l'Eq. (26) peut être utilisé pour obtenir plusieurs paramètres structuraux caractérisant les fractales grasses. Premièrement, le nombre total de minima coïncide avec le nombre total d'itérations fractales. La figure 2 montre que la fractale se compose de trois itérations avec un facteur d'échelle \(\beta _{\mathrm {s}}^{(1)}\) et de trois itérations avec un facteur d'échelle \(\beta _{\mathrm {s} }^{(2)}\). Deuxièmement, à partir de la périodicité de ces minima (ou de la périodicité de I _m (q )q ^D et S _m (q )q ^D ), les facteurs d'échelle peuvent être récupérés. Dans la figure 2 b, le facteur d'échelle \(\beta _{\mathrm {s}}^{(1)}\) peut être obtenu à partir de la périodicité des minima à ql ₀ ≃7,25 et 90, tandis que le facteur d'échelle \(\beta _{\mathrm {s}}^{(2)}\) peut être obtenu à partir de la périodicité des minima à ql ₀ ≃400,1000 et 2500. De plus, la longueur du plateau intermédiaire entre les régions fractales peut être utilisée comme indication du rapport (f ) des distances entre les unités de diffusion et leur taille globale. Sur la figure 2b, cette plage correspond à 13≲ql ₀ ≲130.

Intensité de diffusion polydisperse et facteur de structure

Dans cette partie de notre travail, nous pouvons considérer maintenant que les tailles de réseaux obéissent à une fonction de distribution D _N (l ₀ ), défini de telle sorte que D _N (l ₀ )dl ₀ donne la probabilité que la taille du réseau fractal soit dans l'intervalle (l ₀ ,l ₀ +dl ₀ ). Cette étape introduit la polydispersité dans notre modèle fractal de graisse. Nous illustrons cela en choisissant une distribution log-normale :

$$ D_{\mathrm{N}}(l_{0}) =\frac{1}{\sigma l_{0} (2\pi)^{1/2}}e^{-\frac{\left (\log(l_{0}/\mu)+\sigma^{2}/2\right)^{2}}{2\sigma^{2}}}, $$ (27)

avec variance relative \(\sigma _{\mathrm {r}} =\left (\left \langle l_{0}^{2} \right \rangle _{D} - \mu ^{2}\right)^ {1/2}/\mu \), mean value μ =〈l ₀ 〉 _D , and variance \(\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}\). Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:

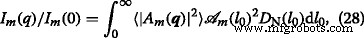
où 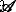is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term 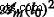[29].

The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ _r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ _r , the positions of main minima and maxima are still observable.

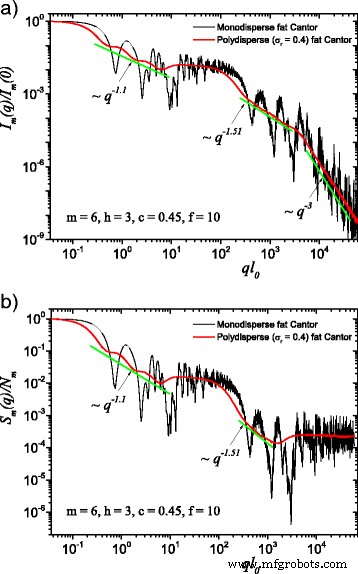
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); b structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql ₀ ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l ₀ =l _in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level

More generally, for small values of σ _r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ _r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.

Conclusions

In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.

Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.

We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.

The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.

Appendix

fractal dimension

Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D _m ).

In general terms, the mass-radius relation can be rewritten as [2]:

where the scaling law correction A (r ) tends to a constant value if r →∞ .

If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l ₀ , composed of k elementary units at the first iteration, each of size β _s l ₀ , where β _s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:

one can write M (l ₀ )=kM (β _s l ₀ ). En utilisant l'éq. (29), one obtains a direct method to compute the fractal dimension, via:

fraunhofer diffraction and the array theorem

Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z direction. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:

In the previous formula, \(r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}\) is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .

Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:

This approximation leads to the Fresnel diffraction integral:

where the prefactor P (u,v ) is given by

et k =2π /λ . Considering, in addition, that the condition z ≫k Max(x ² +y ² )/2 is satisfied, one has \(\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1\). Rewriting Eq. (34), the Fraunhofer approximation becomes:

Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space: