Conversion à partir de la numération décimale

Étant donné que les systèmes de numération octal et hexadécimal ont des bases qui sont des multiples de binaire (base 2), la conversion aller-retour entre hexadécimal ou octal et binaire est très facile.

De plus, étant donné que nous sommes si familiers avec le système décimal, il est relativement facile de convertir une forme binaire, octale ou hexadécimale en forme décimale (additionnez simplement les produits des valeurs chiffrées et des pondérations).

Cependant, la conversion du nombre décimal vers l'un de ces systèmes de numération « étranges » est une autre affaire.

Méthode d'essai et d'ajustement

La méthode qui aura probablement le plus de sens est la méthode « d'essai et d'ajustement », où vous essayez d'« ajuster » la notation binaire, octale ou hexadécimale à la valeur souhaitée telle qu'elle est représentée sous forme décimale.

Par exemple, disons que je voulais représenter la valeur décimale de 87 sous forme binaire. Commençons par dessiner un champ de nombre binaire, complété par des valeurs de pondération :

Eh bien, nous savons que nous n'aurons pas de bit "1" à la place du 128, car cela nous donnerait immédiatement une valeur supérieure à 87.

Cependant, comme le poids suivant à droite (64) est inférieur à 87, nous savons que nous devons y avoir un « 1 ».

Si nous devions également faire de l'emplacement suivant à droite un "1", notre valeur totale serait de 64₁₀ + 32₁₀ , ou 96₁₀ . C'est supérieur à 87₁₀ , nous savons donc que ce bit doit être un "0".

Si nous rendons le bit de position suivant (16) égal à "1", cela porte notre valeur totale à 64₁₀ + 16₁₀ , ou 80₁₀ , ce qui est plus proche de notre valeur souhaitée (87₁₀ ) sans le dépasser :

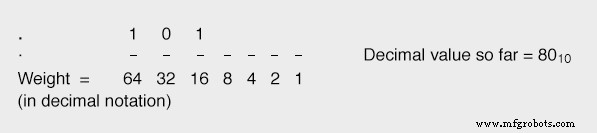
En poursuivant cette progression, en réglant chaque bit de poids moindre car nous devons atteindre notre valeur totale souhaitée sans la dépasser, nous finirons par arriver au chiffre correct :

Méthode d'essai et d'ajustement en octal et hexadécimal

Cette stratégie d'essai et d'ajustement fonctionnera également avec les conversions octales et hexadécimales. Prenons le même chiffre décimal, 87₁₀ , et convertissez-le en numération octale :

Si nous mettons un chiffre de "1" à la place de 64, nous aurions une valeur totale de 64₁₀ (moins de 87₁₀ ). Si nous mettons un chiffre de "2" à la place de 64, nous aurions une valeur totale de 128₁₀ (supérieur à 87₁₀ ). Cela nous indique que notre numération octale doit commencer par un « 1 » à la place du 64 :

Maintenant, nous devons expérimenter avec des valeurs de chiffrement à la place du 8 pour essayer d'obtenir une valeur totale (décimale) aussi proche que possible de 87 sans la dépasser. En essayant les premières options de chiffrement, nous obtenons :

Une valeur chiffrée de "3" à la place de 8 nous placerait au-dessus du total souhaité de 87₁₀ , c'est donc "2" !

Bien sûr, si vous aviez fait attention lors de la dernière section sur les conversions octales/binaires, vous vous rendrez compte qu'on peut prendre la représentation binaire de (décimal) 87₁₀ , que nous avons précédemment déterminé comme étant 1010111₂ , et convertissez-le facilement en octal pour vérifier notre travail :

Pouvons-nous effectuer la conversion décimal en hexadécimal de la même manière ? Bien sûr, mais qui le voudrait ? Cette méthode est simple à comprendre, mais laborieuse à réaliser.

Il existe une autre façon de faire ces conversions, qui est essentiellement la même (mathématiquement), mais plus facile à accomplir.

Technique de division répétée

Cette autre méthode utilise des cycles de division répétés (en utilisant la notation décimale) pour diviser la numération décimale en multiples de valeurs de pondération binaire, octale ou hexadécimale.

Dans le premier cycle de division, nous prenons le nombre décimal d'origine et le divisons par la base du système de numération vers lequel nous convertissons (binaire=2 octal=8, hex=16).

Ensuite, nous prenons la partie entière du résultat de la division (quotient) et la divisons à nouveau par la valeur de base, et ainsi de suite, jusqu'à ce que nous obtenions un quotient inférieur à 1.

Les chiffres binaires, octaux ou hexadécimaux sont déterminés par les « restes » laissés par chaque étape de division. Voyons comment cela fonctionne pour le binaire, avec l'exemple décimal de 87₁₀ :

Les bits binaires sont assemblés à partir des restes des étapes de division successives, en commençant par le LSB et en passant par le MSB. Dans ce cas, nous arrivons à une notation binaire de 1010111₂ .

Lorsque nous divisons par 2, nous obtiendrons toujours un quotient se terminant par ".0" ou ".5", c'est-à-dire un reste de 0 ou 1. Comme cela a été dit précédemment, cette technique de division répétée pour la conversion fonctionnera pour la numération systèmes autres que binaires.

Si nous devions effectuer des divisions successives en utilisant un nombre différent, tel que 8 pour la conversion en octal, nous obtiendrons nécessairement des restes entre 0 et 7. Essayons cela avec le même nombre décimal, 87₁₀ :

Nous pouvons également utiliser une technique similaire pour convertir des systèmes de numération traitant des quantités inférieures à 1.

Pour convertir un nombre décimal inférieur à 1 en binaire, octal ou hexadécimal, nous utilisons une multiplication répétée, en prenant la partie entière du produit à chaque étape comme chiffre suivant de notre nombre converti.

Utilisons le nombre décimal 0.8125₁₀ par exemple, conversion en binaire :

Comme pour le processus de division répétée pour les entiers, chaque étape nous donne le prochain chiffre (ou bit) le plus éloigné du « point ».

Avec un entier (division), on a travaillé du LSB au MSB (de droite à gauche), mais avec des multiplications répétées, on a travaillé de la gauche vers la droite.

Pour convertir un nombre décimal supérieur à 1, avec une composante <1, il faut utiliser les deux techniques, une à la fois. Prenons l'exemple décimal de 54.40625₁₀ , conversion en binaire :

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les systèmes de numération