Ajout de vecteur simple

N'oubliez pas que les vecteurs sont des objets mathématiques tout comme les nombres sur une droite numérique :ils peuvent être additionnés, soustraits, multipliés et divisés. L'addition est peut-être l'opération vectorielle la plus simple à visualiser, nous allons donc commencer par cela. Si des vecteurs avec des angles communs sont ajoutés, leurs magnitudes (longueurs) s'additionnent comme des quantités scalaires régulières :(Figure ci-dessous)

De même, si des sources de tension CA avec le même angle de phase sont connectées ensemble en série, leurs tensions s'additionnent comme on peut s'y attendre avec des batteries CC :(Figure ci-dessous)

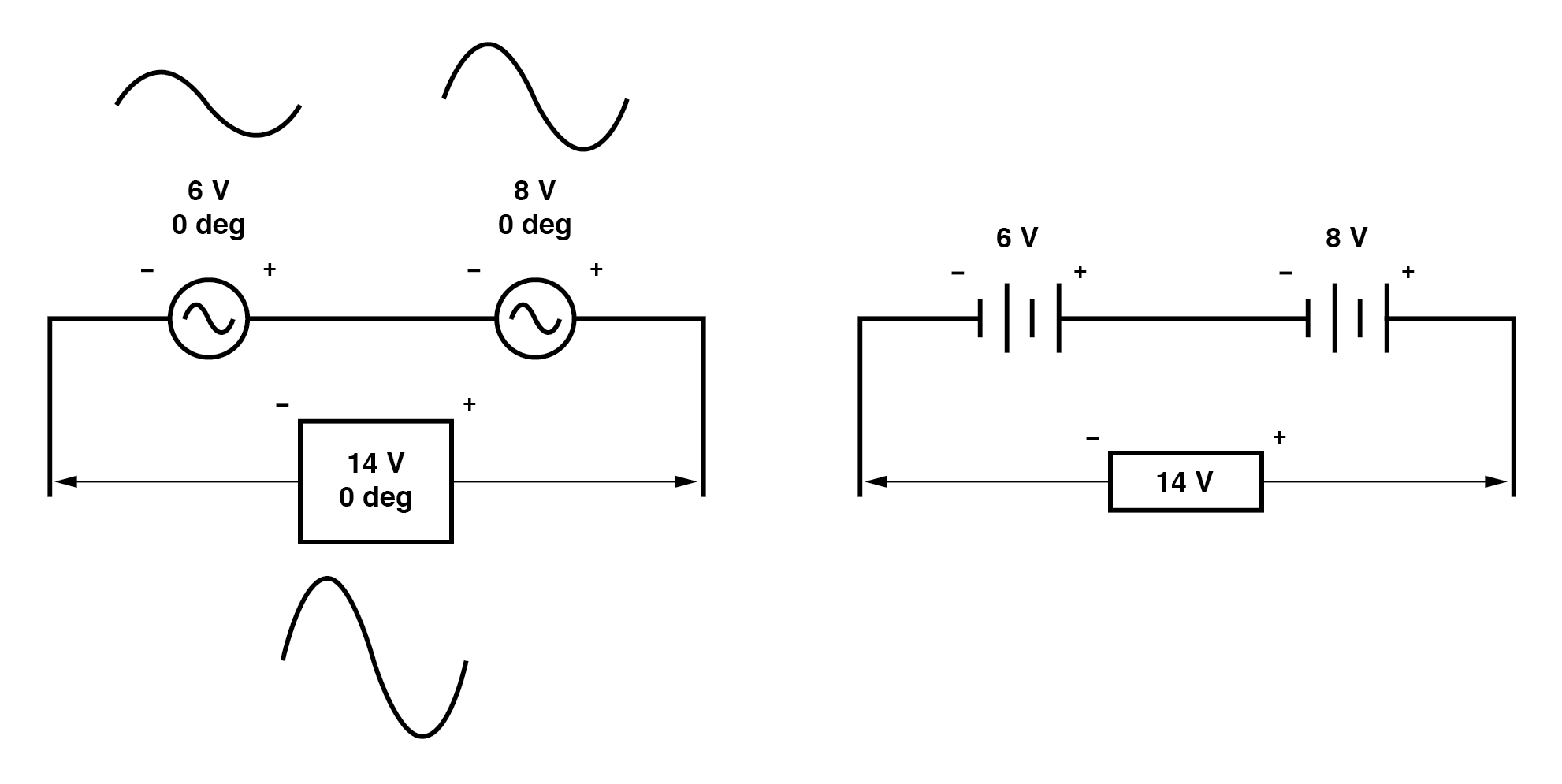
Veuillez noter les marques de polarité (+) et (-) à côté des fils des deux sources CA. Même si nous savons que le courant alternatif n'a pas de « polarité » dans le même sens que le courant continu, ces marques sont essentielles pour savoir comment référencer les angles de phase donnés des tensions. Cela deviendra plus évident dans l'exemple suivant.

Si les vecteurs s'opposent directement (180° déphasé) sont additionnés, leurs amplitudes (longueurs) se soustraient tout comme les quantités scalaires positives et négatives se soustraient lorsqu'elles étaient ajoutées :(Figure ci-dessous)

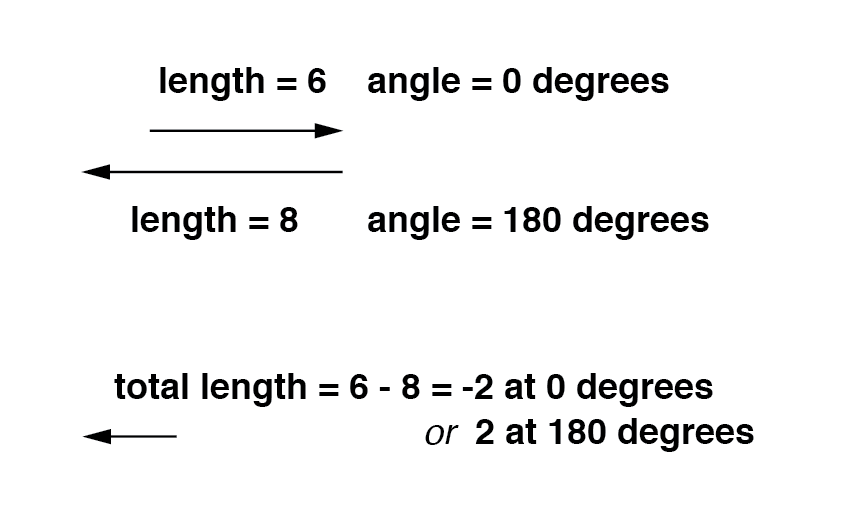
De même, si des sources de tension alternative opposées sont connectées en série, leurs tensions se soustraient comme on peut s'y attendre avec des batteries DC connectées de manière opposée :(Figure ci-dessous)

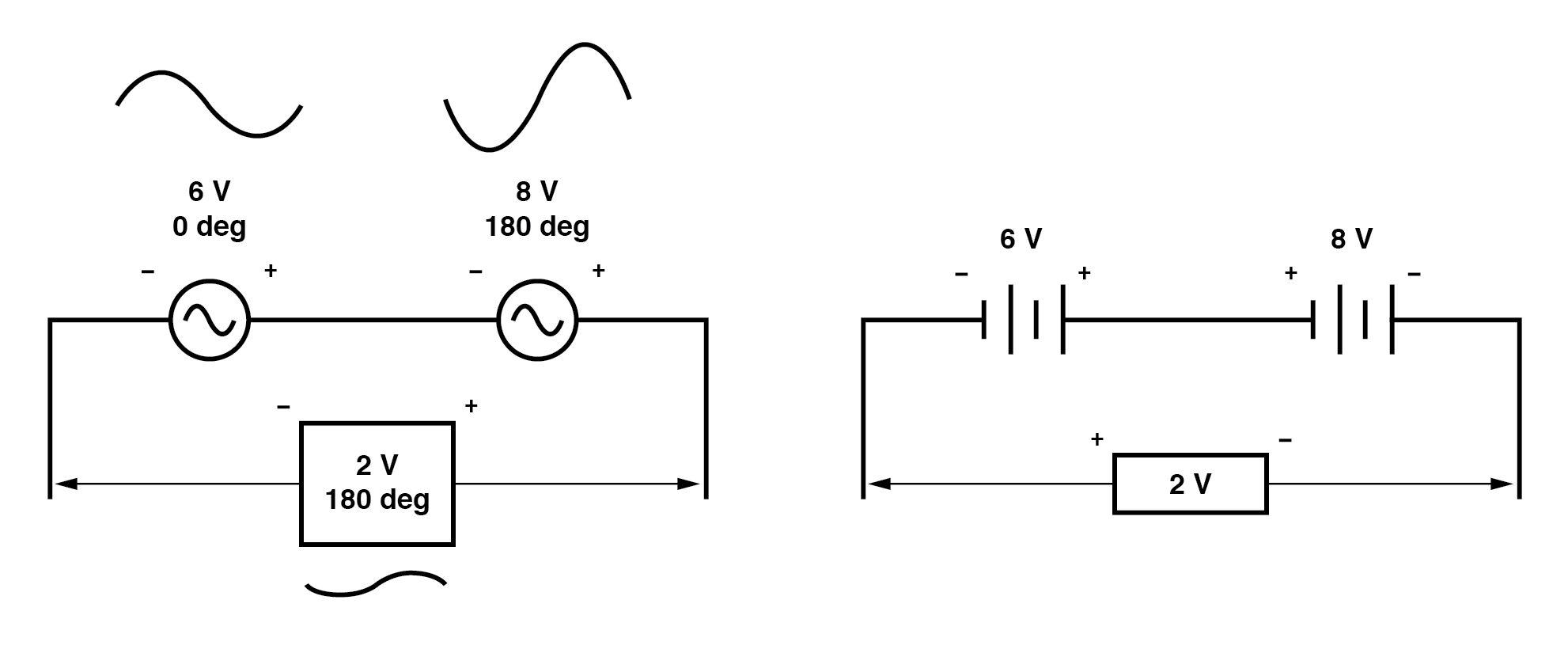
Déterminer si ces sources de tension s'opposent ou non nécessite un examen de leurs marquages ​​de polarité et leurs angles de phase. Remarquez comment les marques de polarité dans le diagramme ci-dessus semblent indiquer des tensions additives (de gauche à droite, nous voyons - et + sur la source 6 volts, - et + sur la source 8 volts).

Même si ces marques de polarité indiqueraient normalement un additif effet dans un circuit CC (les deux tensions travaillant ensemble pour produire une tension totale plus élevée), dans ce circuit CA, elles poussent en fait dans des directions opposées car l'une de ces tensions a un angle de phase de 0° et l'autre un angle de phase de 180° .

Le résultat, bien sûr, est une tension totale de 2 volts.

On aurait tout aussi bien pu montrer les tensions opposées se soustrayant en série comme ceci :(Figure ci-dessous)

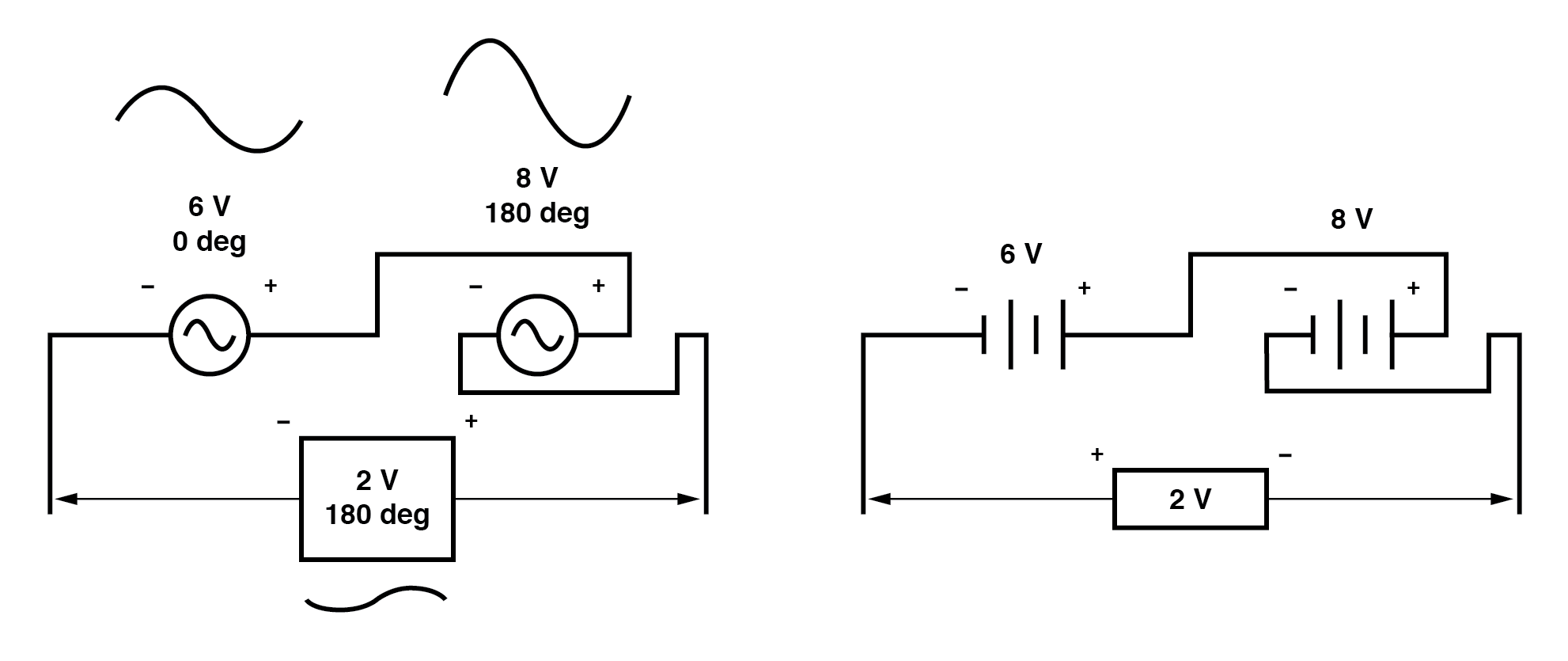
Notez comment les polarités semblent être opposées les unes aux autres maintenant, en raison de l'inversion des connexions des fils sur la source de 8 volts.

Étant donné que les deux sources sont décrites comme ayant des angles de phase égaux (0° ), ils sont vraiment opposés les uns aux autres, et l'effet global est le même que le premier scénario avec des polarités « additives » et des angles de phase différents :une tension totale de seulement 2 volts. (Figure ci-dessous)

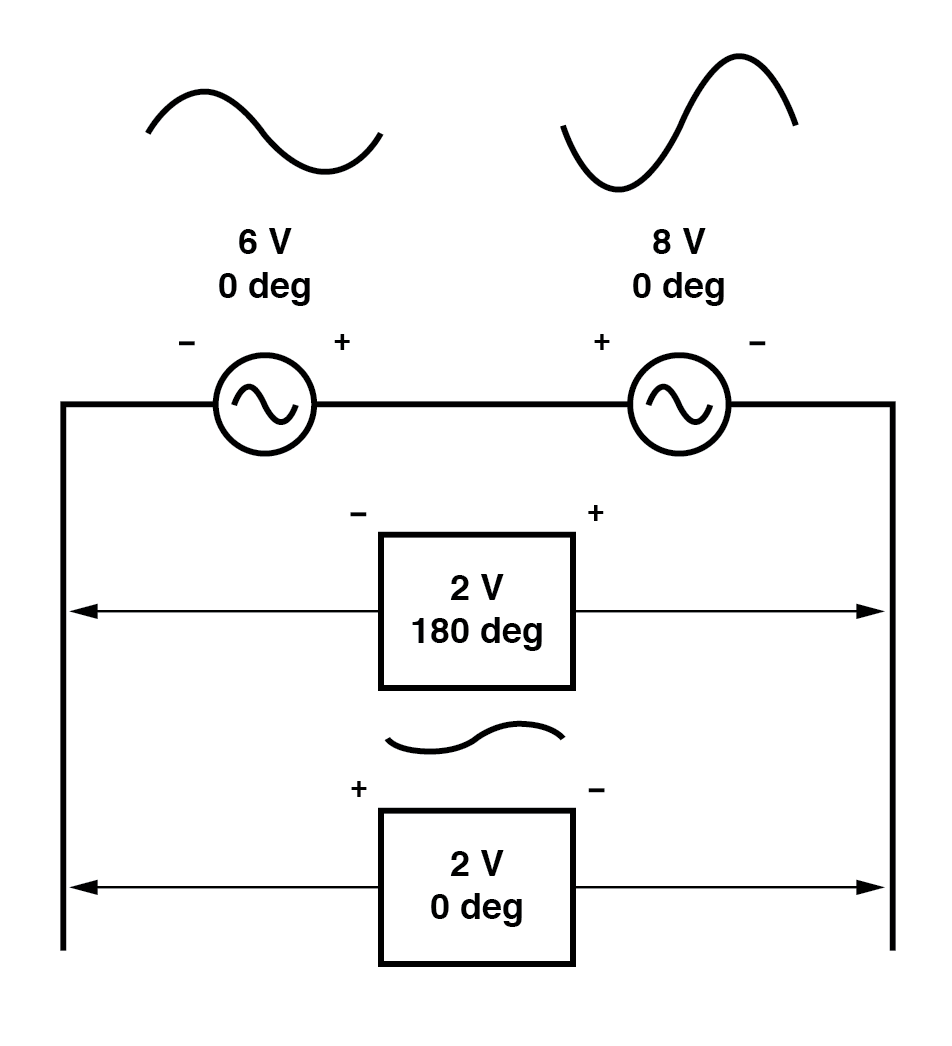
Tout comme il existe deux manières d'exprimer la phase des sources, il existe deux manières d'exprimer la résultante de leur somme.

La tension résultante peut être exprimée de deux manières différentes :2 volts à 180° avec le symbole (-) à gauche et le symbole (+) à droite, ou 2 volts à 0° avec le symbole (+) à gauche et le symbole (-) à droite. Une inversion des fils d'une source de tension alternative équivaut à un déphasage de cette source de 180°. (Figure ci-dessous)

Exemple de sources de tension équivalentes.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail de la phase AC
• Feuille de travail d'analyse du réseau AC