Conversions Δ-Y et Y-Δ

Dans de nombreuses applications de circuits, nous rencontrons des composants connectés ensemble de l'une des deux manières suivantes pour former un réseau à trois bornes :la configuration « Delta » ou Δ (également connue sous le nom de « Pi » ou π) et la configuration « Y » ( également connue sous le nom de configuration « T ».

Il est possible de calculer les valeurs appropriées des résistances nécessaires pour former un type de réseau (Δ ou Y) qui se comporte de manière identique à l'autre type, tel qu'analysé à partir des seules connexions des bornes. C'est-à-dire que si nous avions deux réseaux de résistances distincts, un et un Y, chacun avec ses résistances cachées à la vue, avec rien d'autre que les trois bornes (A, B et C) exposées pour les tests, les résistances pourraient être dimensionnées pour le deux réseaux de sorte qu'il n'y aurait aucun moyen de déterminer électriquement un réseau indépendamment de l'autre. En d'autres termes, les réseaux équivalents Δ et Y se comportent de manière identique.

Équations de conversion Δ et Y

Il existe plusieurs équations utilisées pour convertir un réseau en un autre :

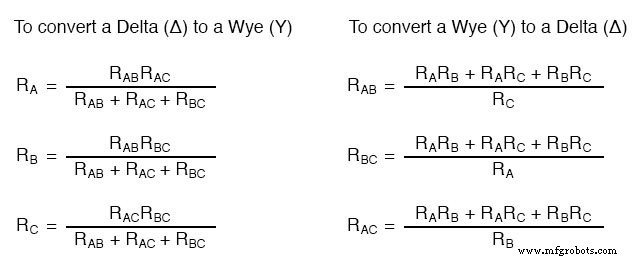
Les réseaux Δ et Y sont fréquemment observés dans les systèmes d'alimentation CA triphasés (un sujet traité dans le volume II de cette série de livres), mais même alors, ce sont généralement des réseaux équilibrés (toutes les résistances sont de valeur égale) et la conversion de l'un à l'autre n'implique pas nécessairement des calculs aussi complexes. Quand le technicien moyen aurait-il besoin d'utiliser ces équations ?

Application de la conversion Δ et Y

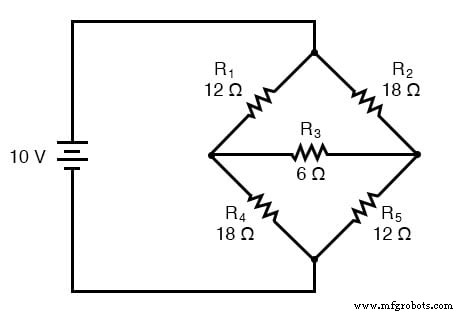
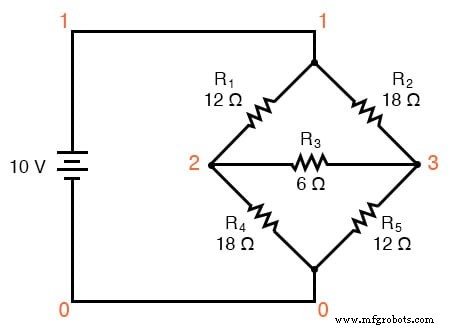
Une application principale de la conversion Δ-Y réside dans la solution des circuits en pont non équilibrés, comme celui ci-dessous :

La solution de ce circuit avec l'analyse du courant de branche ou du courant de maille est assez complexe, et ni les théorèmes de Millman ni de superposition ne sont d'aucune utilité car il n'y a qu'une seule source d'alimentation. On pourrait utiliser le théorème de Thevenin ou de Norton, en traitant R₃ comme notre charge, mais qu'est-ce que ce serait amusant ?

Si on devait traiter les résistances R₁ , R₂ , et R₃ comme étant connecté dans une configuration (R_ab , R_ac , et R_bc , respectivement) et générer un réseau Y équivalent pour les remplacer, nous pourrions transformer ce circuit en pont en un circuit combiné série/parallèle (plus simple) :

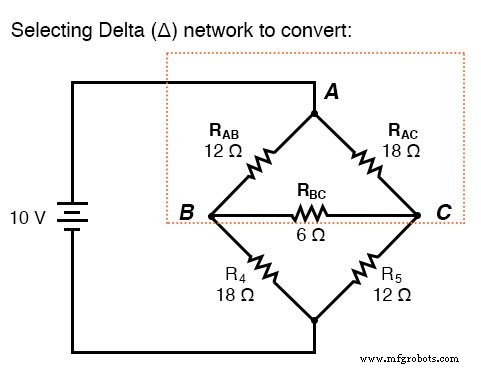
Après la conversion Δ-Y . . .

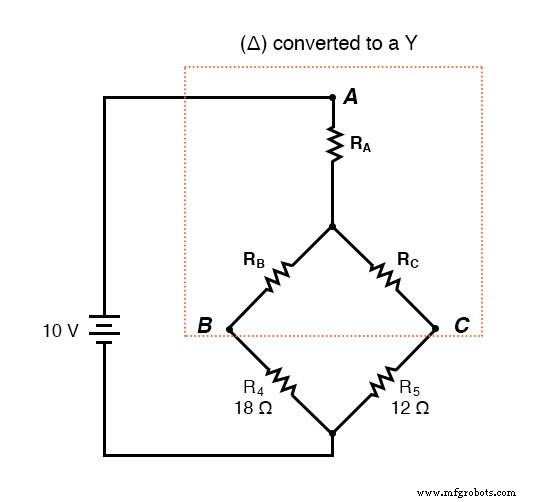
Si nous effectuons nos calculs correctement, les tensions entre les points A, B et C seront les mêmes dans le circuit converti que dans le circuit d'origine, et nous pouvons transférer ces valeurs vers la configuration de pont d'origine.

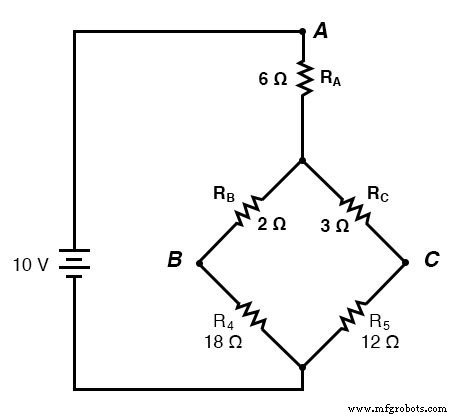
Résistances R₄ et R₅ , bien sûr, restent les mêmes à 18 et 12 Ω, respectivement. En analysant maintenant le circuit comme une combinaison série/parallèle, nous arrivons aux chiffres suivants :

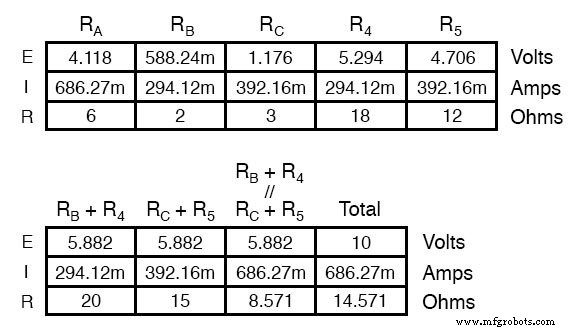
Nous devons utiliser les chiffres des chutes de tension du tableau ci-dessus pour déterminer les tensions entre les points A, B et C, en voyant comment elles s'additionnent (ou se soustraient, comme c'est le cas avec la tension entre les points B et C) :

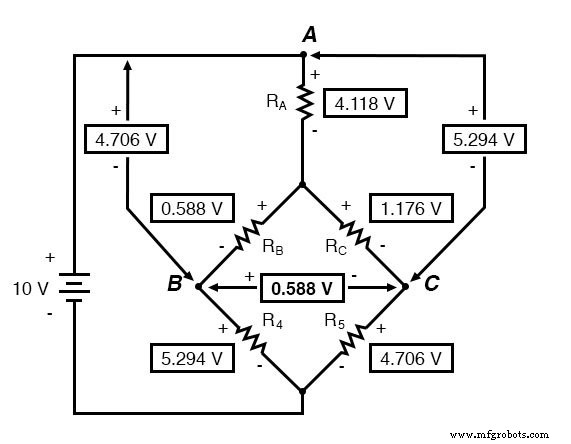
Maintenant que nous connaissons ces tensions, nous pouvons les transférer aux mêmes points A, B et C dans le circuit en pont d'origine :

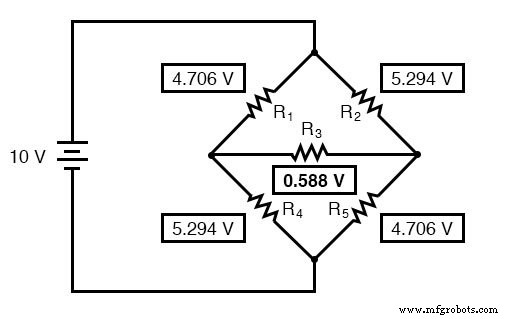
Chutes de tension sur R₄ et R₅ , bien sûr, sont exactement les mêmes que dans le circuit du convertisseur.

À ce stade, nous pourrions prendre ces tensions et déterminer les courants de résistance grâce à l'utilisation répétée de la loi d'Ohm (I=E/R) :

Simulation à l'aide de SPICE

Une simulation rapide avec SPICE servira à vérifier notre travail :