Conductance

Lorsque les élèves voient pour la première fois l'équation de résistance parallèle, la question naturelle à se poser est :« Où est-ce que ce la chose vient ? C'est vraiment une étrange pièce d'arithmétique, et son origine mérite une bonne explication.

Quelle est la différence entre la résistance et la conductance ?

La résistance, par définition, est la mesure du frottement un composant présente à la circulation du courant à travers elle. La résistance est symbolisée par la lettre majuscule « R » et est mesurée dans l'unité « ohm ». Cependant, nous pouvons également penser à cette propriété électrique en termes de son inverse :comment facile c'est pour le courant de circuler à travers un composant, plutôt que comment difficile .

Si résistance est le mot que nous utilisons pour symboliser la mesure de la difficulté pour le courant à circuler, alors un bon mot pour exprimer à quel point il est facile pour le courant de circuler serait conductance . Mathématiquement, la conductance est l'inverse, ou l'inverse, de la résistance :

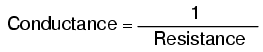
Plus la résistance est élevée, moins la conductance est élevée, et vice versa.

Cela devrait avoir un sens intuitif car la résistance et la conductance sont des moyens opposés pour désigner la même propriété électrique essentielle.

Si les résistances de deux composants sont comparées et qu'il s'avère que le composant « A » a la moitié de la résistance du composant « B », alors nous pourrions alternativement exprimer cette relation en disant que le composant « A » est deux fois aussi conducteur que le composant « B ». Si le composant "A" n'a qu'un tiers de la résistance du composant "B", alors nous pourrions dire qu'il est trois fois plus conducteur que le composant « B » et ainsi de suite.

L'unité de conductance

Pour aller plus loin dans cette idée, un symbole et une unité ont été créés pour représenter la conductance. Le symbole est la lettre majuscule « G » et l'unité est le mho , qui est « ohm » épelé à l'envers (et vous ne pensiez pas que les ingénieurs en électronique avaient le sens de l'humour !).

Malgré sa pertinence, l'unité de la mho a été remplacée dans les années suivantes par l'unité de Siemens (abrégé par la lettre majuscule « S »). Cette décision de changer de nom d'unité rappelle le changement d'unité de température en degrés Centigrade en degrés Celsius , ou le changement de l'unité de fréquence c.p.s. (cycles par seconde) à Hertz . Si vous cherchez un modèle ici, Siemens, Celsius et Hertz sont tous des noms de famille de scientifiques célèbres, dont les noms, malheureusement, nous en disent moins sur la nature des unités que les désignations originales des unités.

En note de bas de page, l'unité de Siemens n'est jamais exprimée sans la dernière lettre « s ». En d'autres termes, il n'existe pas d'unité de « siemen » comme dans le cas du « ohm » ou du « mho ». La raison en est l'orthographe correcte des noms de famille des scientifiques respectifs.

L'unité de résistance électrique a été nommée d'après une personne nommée "Ohm", tandis que l'unité de conductance électrique a été nommée d'après une personne nommée "Siemens", il serait donc inapproprié de "singulariser" cette dernière unité car son "s" final ne désigne pas pluralité.

De retour à notre exemple de circuit parallèle, nous devrions être en mesure de voir que plusieurs chemins (branches) pour le courant réduisent la résistance totale pour l'ensemble du circuit, car le courant peut circuler plus facilement à travers l'ensemble du réseau de plusieurs branches que par l'un des ces résistances de branche seules. En termes de résistance , des branches supplémentaires donnent un total moindre (le courant rencontre moins d'opposition). En termes de conductance , cependant, des branches supplémentaires entraînent un total plus élevé (le courant circule avec une plus grande conductance).

Résistance parallèle totale

La résistance parallèle totale est inférieure que l'une des résistances de branche individuelles, car les résistances parallèles résistent moins ensemble qu'elles ne le feraient séparément :

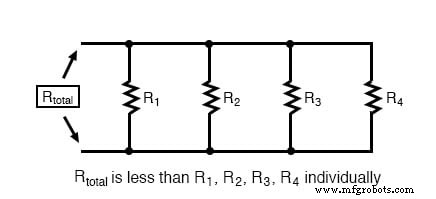
Conductance Parallèle Totale

La conductance parallèle totale est plus grande que n'importe laquelle des conductances de branche individuelles, car les résistances parallèles conduisent mieux ensemble qu'elles ne le feraient séparément :

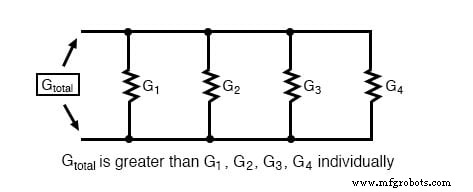
Pour être plus précis, la conductance totale dans un circuit parallèle est égale à la somme des conductances individuelles :

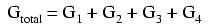
Si nous savons que la conductance n'est rien de plus que l'inverse mathématique (1/x) de la résistance, nous pouvons traduire chaque terme de la formule ci-dessus en résistance en substituant l'inverse de chaque conductance respective :

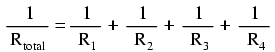
En résolvant l'équation ci-dessus pour la résistance totale (au lieu de l'inverse de la résistance totale), nous pouvons inverser (inverser) les deux côtés de l'équation :

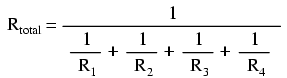
Ainsi, nous arrivons enfin à notre formule de résistance cryptique ! La conductance (G) est rarement utilisée comme mesure pratique, et la formule ci-dessus est donc courante dans l'analyse des circuits parallèles.

AVIS :

• La conductance est l'opposé de la résistance :la mesure de la facile c'est pour que le courant électrique circule à travers quelque chose.
• La conductance est symbolisée par la lettre « G » et est mesurée en unités de mhos ou Siemens .
• Mathématiquement, la conductance est égale à l'inverse de la résistance :G =1/R

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur la loi d'Ohm
• Fiche de travail sur la résistance spécifique des conducteurs