Débordement binaire

Une mise en garde avec les nombres binaires signés est celle du débordement, où la réponse à un problème d'addition ou de soustraction dépasse la grandeur qui peut être représentée avec le nombre de bits alloué. N'oubliez pas que la place du bit de signe est fixée dès le début du problème.

Avec le dernier exemple de problème, nous avons utilisé cinq bits binaires pour représenter l'amplitude du nombre, et le bit le plus à gauche (sixième) comme bit de poids négatif, ou de signe. Avec cinq bits pour représenter la magnitude, nous avons une plage de représentation de 2 ⁵ , soit trente-deux pas entiers de 0 au maximum.

Cela signifie que nous pouvons représenter un nombre aussi élevé que +31₁₀ (011111₂ ), ou aussi bas que -32₁₀ (100000₂ ).

Restrictions du champ numérique à six bits

Si nous mettons en place un problème d'addition avec deux nombres binaires, le sixième bit utilisé pour le signe, et le résultat dépasse +31₁₀ ou est inférieur à -32₁₀ , notre réponse sera incorrecte. Essayons d'ajouter 17₁₀ et 19₁₀ pour voir comment fonctionne cette condition de débordement pour les nombres positifs excessifs :

La réponse (100100₂ ), interprété avec le sixième bit comme -32₁₀ place, est en fait égal à -28₁₀ , pas +36₁₀ comme nous devrions l'obtenir avec +17₁₀ et +19₁₀ additionnés ! De toute évidence, ce n'est pas correct. Qu'est-ce qui s'est mal passé ?

La réponse réside dans les restrictions du champ numérique à six bits dans lequel nous travaillons Depuis l'ampleur de la somme vraie et appropriée (36₁₀ ) dépasse la limite autorisée pour notre champ de bits désigné, nous avons une erreur de débordement .

En termes simples, six emplacements ne donnent pas assez de bits pour représenter la somme correcte, donc quel que soit le chiffre que nous obtenons en utilisant la stratégie consistant à rejeter le bit « carry » le plus à gauche sera incorrect.

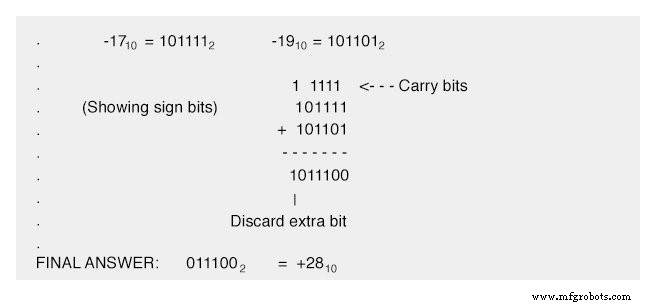
Une erreur similaire se produira si nous ajoutons deux nombres négatifs pour produire une somme trop faible pour notre champ binaire de six bits. Essayons d'ajouter -17₁₀ et -19₁₀ ensemble pour voir comment cela fonctionne (ou ne fonctionne pas, selon le cas !) :

La réponse (incorrecte) est positive vingt-huit. Le fait que la somme réelle de moins dix-sept et moins dix-neuf était trop faible pour être correctement représentée avec un champ d'amplitude de cinq bits et un sixième bit de signe est à l'origine de cette difficulté.

Utiliser le septième bit pour un bit de signe

Essayons à nouveau ces deux problèmes, sauf cette fois en utilisant le septième bit pour un bit de signe, et en permettant l'utilisation de 6 bits pour représenter la magnitude :

En utilisant des champs de bits suffisamment grands pour gérer l'amplitude des sommes, nous arrivons aux réponses correctes. Dans ces exemples de problèmes, nous avons pu détecter les erreurs de débordement en effectuant les problèmes d'addition sous forme décimale et en comparant les résultats avec les réponses binaires.

Par exemple, lors de l'ajout de +17₁₀ et +19₁₀ ensemble, nous savions que la réponse était supposée être +36₁₀ , donc quand la somme binaire vérifiée est -28₁₀ , nous savions que quelque chose n'allait pas. Bien qu'il s'agisse d'un moyen valable pour détecter les débordements, il n'est pas très efficace.

Après tout, l'idée même de la complémentation est de pouvoir additionner de manière fiable des nombres binaires et de ne pas avoir à revérifier le résultat en additionnant les mêmes nombres sous forme décimale ! Cela est particulièrement vrai dans le but de construire des circuits électroniques pour additionner des quantités binaires :le circuit doit être capable de vérifier lui-même le débordement sans la supervision d'un être humain qui sait déjà quelle est la bonne réponse.

Ce dont nous avons besoin, c'est d'une méthode de détection d'erreurs simple qui ne nécessite aucune arithmétique supplémentaire. La solution la plus élégante est peut-être de rechercher le signe de la somme et comparez-la aux signes des nombres ajoutés.

Évidemment, deux nombres positifs additionnés devraient donner un résultat positif, et deux nombres négatifs additionnés devraient donner un résultat négatif. Notez que chaque fois que nous avions une condition de débordement dans les problèmes d'exemple, le signe de la somme était toujours opposé des deux nombres ajoutés :+17₁₀ plus +19₁₀ donnant -28₁₀ , ou -17₁₀ plus -19₁₀ donnant +28₁₀ .

En vérifiant uniquement les signes, nous pouvons dire que quelque chose ne va pas. Mais qu'en est-il des cas où un nombre positif est ajouté à un nombre négatif ? De quel signe doit être la somme pour être correcte. Ou, plus précisément, quel signe de somme indiquerait nécessairement une erreur de débordement ?

La réponse à cette question est tout aussi élégante :il n'y aura jamais être une erreur de débordement lorsque deux nombres de signes opposés sont additionnés ! La raison en est évidente lorsque l'on considère la nature du débordement. Un débordement se produit lorsque l'amplitude d'un nombre dépasse la plage autorisée par la taille du champ de bits.

La somme de deux nombres signés de manière identique peut très bien dépasser la plage du champ de bits de ces deux nombres, et donc dans ce cas un débordement est une possibilité. Cependant, si un nombre positif est ajouté à un nombre négatif, la somme sera toujours plus proche de zéro que l'un ou l'autre des deux nombres ajoutés :sa grandeur doit être inférieur à l'amplitude de l'un ou l'autre des nombres d'origine, et le débordement est donc impossible.

Heureusement, cette technique de détection de débordement est facilement implémentée dans les circuits électroniques, et c'est une caractéristique standard dans les circuits additionneurs numériques :un sujet pour un chapitre ultérieur.

FICHES DE TRAVAIL CONNEXES :

• Feuille d'exercices de mathématiques binaires