Numération décimale contre numération binaire

Comptons de zéro à vingt en utilisant quatre types différents de systèmes de numération :dièses, chiffres romains, décimal et binaire :

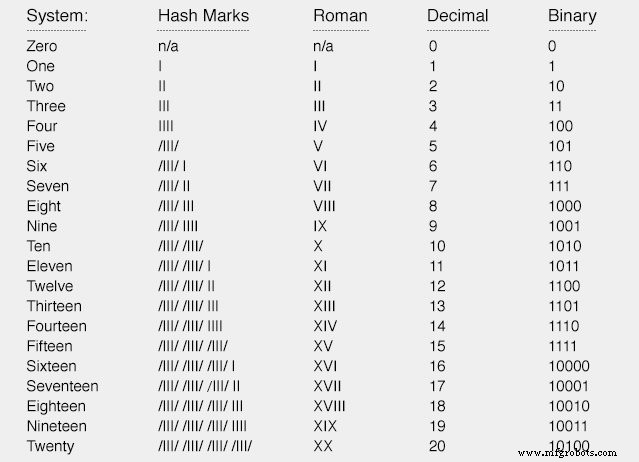
Ni les dièses ni le système romain ne sont très pratiques pour symboliser les grands nombres. De toute évidence, les systèmes pondérés tels que décimal et binaire sont plus efficaces pour la tâche.

Notez, cependant, combien la notation décimale est plus courte que la notation binaire, pour le même nombre de quantités. Ce qui prend cinq bits en notation binaire ne prend que deux chiffres en notation décimale.

Cela soulève une question intéressante concernant les différents systèmes de numération :quelle taille d'un nombre peut être représentée avec un nombre limité de positions de chiffrement, ou de places ? Avec le système de hachage brut, le nombre de places EST le plus grand nombre qui peut être représenté, puisqu'un signe dièse « place » est requis pour chaque étape entière.

Pour les systèmes de numération pondérés en place, cependant, la réponse est trouvée en prenant la base du système de numération (10 pour décimal, 2 pour binaire) et en l'élevant à la puissance du nombre de places.

Par exemple, 5 chiffres dans un système de numération décimal peuvent représenter 100 000 valeurs de nombres entiers différents, de 0 à 99 999 (10 à la puissance 5 =100 000). 8 bits dans un système de numération binaire peuvent représenter 256 valeurs de nombres entiers différents, de 0 à 11111111 (binaire) ou de 0 à 255 (décimal), car 2 à la puissance 8 est égal à 256.

Avec chaque position de lieu supplémentaire au champ numérique, la capacité de représentation des nombres augmente d'un facteur de la base (10 pour décimal, 2 pour binaire).

Une note de bas de page intéressante pour ce sujet est l'un des premiers ordinateurs numériques électroniques, l'Eniac.

Les concepteurs de l'Eniac ont choisi de représenter les nombres sous forme décimale, numériquement, en utilisant une série de circuits appelés « compteurs en anneau » au lieu d'utiliser simplement le système de numération binaire, dans le but de minimiser le nombre de circuits nécessaires pour représenter et calculer très grands nombres.

Cette approche s'est avérée contre-productive, et pratiquement tous les ordinateurs numériques depuis lors ont été de conception purement binaire.

Conversion binaire en décimal

Pour convertir un nombre en numération binaire en son équivalent sous forme décimale, il suffit de calculer la somme de tous les produits de bits avec leurs constantes de pondération respectives. Pour illustrer :

Le bit le plus à droite est appelé le bit le moins significatif (LSB), car il se trouve à la place du poids le plus faible (celui de un).

Le bit le plus à gauche est appelé le bit le plus significatif (MSB), car il se situe à la place du poids le plus élevé (le cent vingt-huit).

N'oubliez pas qu'une valeur binaire de « 1 » signifie que le poids de position respectif est ajouté à la valeur totale, et une valeur de bits de « 0 » signifie que le poids de position respectif ne pas être ajouté à la valeur totale. Avec l'exemple ci-dessus, nous avons :

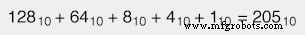
Si nous rencontrons un nombre binaire avec un point (.), appelé « point binaire » au lieu d'un point décimal, nous suivons la même procédure, en réalisant que chaque poids de position à droite du point est la moitié de la valeur du un à gauche de celui-ci (tout comme chaque place poids à droite d'un décimal point est un dixième du poids de celui à sa gauche). Par exemple :

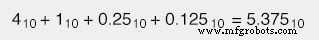
FICHES DE TRAVAIL CONNEXES :

• Feuille d'exercices de mathématiques binaires