Magnétisme de percolation dans les nanoparticules ferroélectriques

Contexte

La fabrication et des études intensives de nanoparticules à partir d'oxydes diélectriques, qui sont non magnétiques en masse, ont révélé le ferromagnétisme qu'elles contiennent, par exemple dans HfO₂ [1], TiO₂ [2,3,4], ZnO [5,6,7], SnO₂ [7, 8], KTaO₃ [9], et KNbO₃ [dix]. Différentes origines des phénomènes ont été considérées, telles que les amas métalliques, les phases secondaires, les polarons magnétiques liés, les porteurs de charge et les lacunes d'oxygène [2, 3, 5, 8,9,10,11,12,13]. Ces dernières s'hybrident au voisinage de la surface des nanoparticules, acquérant ainsi des propriétés magnétiques [12, 13]. Actuellement, les explications sont encore controversées et il n'y a pas de consensus sur la source du ferromagnétisme. Par conséquent, l'activité de recherche se poursuit dans la direction.

Parmi les ferroélectriques, récemment, dans les nanocristaux (la taille moyenne des particules est de 80 nm) de tantalate de potassium et de niobate de potassium, produits par la nouvelle technologie d'oxygénation du métal (Ta ou Nb) dans le nitrate de potassium fondu [14], les méthodes de résonance magnétique et d'aimantation statique ont établi expérimentalement l'apparition d'un sous-système ferromagnétique avec un sous-système paramagnétique [10, 15, 16]. Cet effet est absent dans les cristaux plus gros (avec des tailles> 200 nm) des composés obtenus par la même technologie. Les composés sont non magnétiques dans la masse. Le dopage intentionnel du tantalate de potassium (KNbO₃ ) et le niobate de potassium (KTaO₃ ) les nanocristaux de fer et de manganèse ont entraîné séparément l'augmentation de la composante paramagnétique, tandis que le sous-système ferromagnétique reste inchangé [15, 16]. Il a été suggéré que la raison de l'apparition des propriétés magnétiques des nanocristaux ferroélectriques vierges est due à des défauts magnétiques, qui peuvent être à la fois des atomes d'impuretés de fer, formant des amas métalliques à la surface des nanoparticules, et des lacunes d'oxygène [9]. En plus des méthodes expérimentales mentionnées ci-dessus, cette hypothèse était basée sur les données de l'analyse élémentaire et des estimations théoriques.

Afin de déterminer le mécanisme microscopique du phénomène observé, dans ce travail, nous analysons la situation à l'aide d'une théorie de la percolation. La théorie de la percolation a assez bien décrit un certain nombre d'effets dans les systèmes magnétiques désordonnés, plus tôt dans les ferrodiélectriques [17], plus tard dans les semi-conducteurs magnétiques dilués (par exemple, [18,19,20,21]). Le sous-système magnétique est traité comme un polaron magnétique lié dans les semi-conducteurs dilués. Ce modèle a d'abord été proposé par les auteurs de [22] puis développé par les auteurs de Refs. [11, 23].

En supposant le rôle dominant des lacunes d'oxygène, nous utilisons le modèle des polarons magnétiques liés et trouvons le rayon de percolation auquel les interactions d'échange entre les électrons piégés dans les lacunes d'oxygène médiées par les ions d'impuretés magnétiques induisent un ordre ferromagnétique de surface dans le ferroélectrique KTaO_{3 et KNbO3 nanoparticules.}

Données expérimentales et modèle d'ordre ferromagnétique

Afin de justifier le modèle proposé d'ordre ferromagnétique, dans un premier temps, nous exposons les données expérimentales obtenues sur les nanoparticules ferroélectriques КTaO₃ (KTO) et KNbO₃ (SAVEZ).

Les nanoparticules ferroélectriques examinées sont nominalement pures, c'est-à-dire qu'aucun dopant n'a été spécialement incorporé. Cependant, l'analyse élémentaire réalisée avec un spectromètre d'émission atomique à plasma à couplage inductif Shimadzu ICPE-9000 (ICP-AES) montre que Fe est présent dans les deux matériaux en tant qu'impureté inévitable à raison de 0,06 mol.% dans КTaO₃ et 0,008 % mol. dans KNbO₃ . On sait aussi que les lacunes d'oxygène existent toujours dans les oxydes ferroélectriques, comme le type pérovskite (formule générale ABO₃ ), ce qui entraîne un certain degré de non-stoechiométrie dans ces composés. Il a été montré expérimentalement que deux sous-systèmes magnétiques (paramagnétique et ferromagnétique) sont présents dans les nanocristaux KTaO₃ et KNbO₃ [9, 10, 15]. Le sous-système paramagnétique se compose de Fe ³⁺ magnétiques distincts sans interaction ions dans KTaO₃ , et Fe ³⁺ et Mn ²⁺ ions dans KNbO₃ . De plus, la structure du centre paramagnétique, telle que déterminée à partir des mesures de résonance paramagnétique électronique (RPE), comprend une lacune d'oxygène V(O), qui abaisse la symétrie du centre [9, 15]. A titre illustratif, deux types de centres paramagnétiques, de symétrie axiale et rhombique, dans lesquels Fe ³⁺ ion remplace Ta ⁵⁺ (ou Nb ⁵⁺ ), sont illustrés à la Fig. 1. Pour atteindre la compensation de charge, une (centre axial) ou deux (centre rhombique) lacunes d'oxygène V(O) sont formées dans la structure de ces centres.

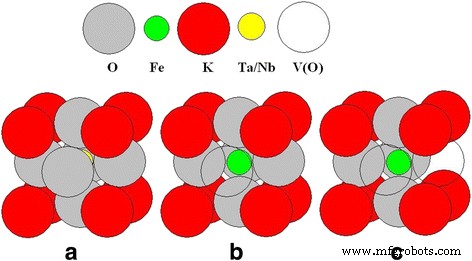
Modèles de centres paramagnétiques à faible symétrie de Fe ³⁺ en KTaO₃ et KNbO₃ nanocristaux. un Cellule unitaire sans défauts, b Fe ³⁺ axiale -V(O) centre, et c Fe ³⁺ rhombique -2 Centre V(O)

Comme suggéré dans les articles [9, 15], le sous-système ferromagnétique est un ou plusieurs amas de surface constitués d'atomes de fer et de lacunes d'oxygène. Le recuit thermique dans une atmosphère d'oxygène, réalisé dans l'article [9], montre que les lacunes d'oxygène contribuent certainement à la formation de ferromagnétisme dans ces composés. D'un côté, les lacunes s'hybrident et deviennent magnétiques près de la surface des nanoparticules [13]. D'un autre côté, les électrons qui émergent de manière inhérente dans les oxydes non stoechiométriques sont souvent piégés par des lacunes d'oxygène. Dans les deux cas, la lacune d'oxygène a le spin S = ½ et porte le moment magnétique correspondant.

La présence de ferromagnétisme de surface a été confirmée expérimentalement par microscopie à force atomique (AFM) en mode gradient de champ magnétique. Par exemple, la Fig. 2 montre les images de surface obtenues pour l'échantillon de KTaO₃ nanocristallin . Les mesures de microscopie à force magnétique (MFM) ont été effectuées par le microscope à sonde à balayage Dimension 3000 NanoScope IIIa pour cartographier la variation spatiale de la structure de magnétisation de la composante hors plan du champ magnétique parasite du KTaO₃ surface de l'échantillon. Les gradients de force magnétique ont été mesurés à l'aide de la technique à deux passes (mode lift) où la topographie a été balayée au premier passage en mode tapping, puis les gradients de champ magnétique ont été cartographiés au second en utilisant le décalage de fréquence d'oscillation de la sonde se déplaçant sur la surface (lift la hauteur était de 300 nm). Les sondes de force magnétique Veeco (MESP) revêtues de cobalt avec une coercivité de ~400 Oe, moment magnétique de 1 · 10 ⁻¹³ l'emu et le rayon nominal de l'apex de la pointe de 25 nm ont été utilisés. Avant les mesures, la sonde était magnétisée à l'aide d'un puissant aimant permanent avec le champ aligné le long de l'axe vertical de la pointe.

Images de surface avec des régions magnétisées dans le KTaO₃ nanocristaux. un Cartographie du gradient de champ magnétique et b image en relief de surface

Aussi, les boucles d'aimantation statique ont été obtenues expérimentalement à deux températures pour chaque composé, à 290 et 150 K pour KTaO₃ et à 290 et 110 K pour KNbO₃ . Les courbes expérimentales d'aimantation sont décrites par la formule :

Ici, M _S est l'aimantation à saturation, H est un champ magnétique statique, et V ₀ est le volume d'un amas magnétique infini (en fait fermé sur une surface de nanoparticules). L'aimantation à saturation a été définie selon la formule (7) de [20] :

où S ₁ et S ₂ sont V(O) et Fe ³⁺ moments magnétiques (spins de V(O) et Fe ³⁺ sont 1/2 et 5/2, respectivement), N ₁ et N ₂ sont les nombres de V(O) et Fe, respectivement. Valeurs données N ₂ correspondent aux concentrations 0,06 % mol. pour le KTO et 0,008 % mol. pour le KNO obtenues à partir de l'analyse élémentaire, les valeurs N ₁ ont été déterminés en conséquence. Les résultats d'ajustement sont montrés dans la Fig. 3. Pour une description des boucles d'hystérésis à faibles champs magnétiques, nous avons utilisé le décalage de la formule (2) sur la valeur du champ coercitif, H _c . Les paramètres de chaque courbe sont indiqués dans le tableau 1.

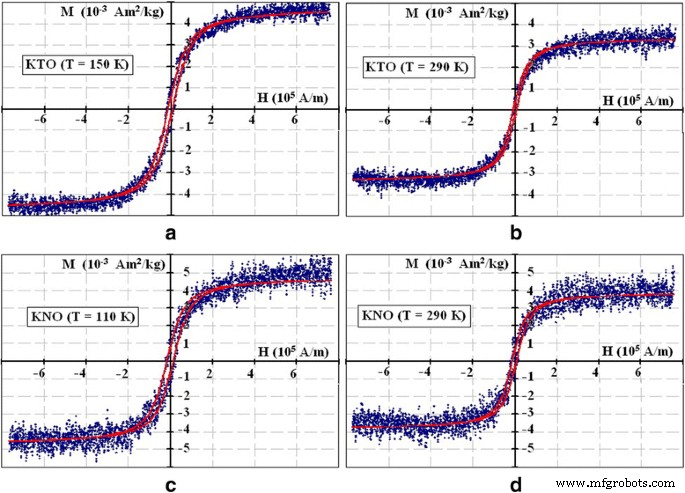
Courbes de magnétisation statique. Courbes de magnétisation en KTaO₃ (un , b ) et KNbO₃ (c , d ) nanoparticules à T = 150, 290, 110 et 290 K. Les paramètres d'ajustement sont répertoriés dans le tableau 1

Selon le nombre de spins magnétiques estimé à partir des données EPR [10, 15], le rapport en pourcentage entre les sous-systèmes paramagnétique et ferromagnétique est de 14/86 dans le tantalate de potassium nanométrique, et il est de 40/60 pour le niobate de potassium. Le plus grand nombre de centres paramagnétiques dans le niobate de potassium est causé par la présence d'impureté de manganèse incontrôlée en plus de l'impureté de fer. Notez que le nombre de spins magnétiques formant le sous-système ferromagnétique, obtenu à partir d'expériences précédentes, n'est pas suffisant pour établir un ordre magnétique à longue distance dans tout le volume des nanoparticules. Par conséquent, nous supposons que la principale contribution au ferromagnétisme sont les spins magnétiques, qui sont près de la surface des particules, à savoir dans la couche souterraine enrichie de défauts. Comme indiqué dans [24], la couche superficielle enrichie de défauts polaires a une épaisseur d'environ 10 constantes de réseau. En revanche, les auteurs de la Réf. [25] suggèrent que la couche enrichie de défauts magnétiques dans le cristal semi-infini a une épaisseur de 1 constante de réseau. Étant donné que les complexes Fe ³⁺ -V(O) sont à la fois des défauts polaires et magnétiques, nous supposons que la couche de défauts près de la surface est de 5 constantes de réseau dans nos calculs. En KTaO₃ et KNbO₃ , la couche correspond à 2 nm. Afin d'utiliser les conditions de percolation dérivées dans l'article [17], nous supposons que la distribution des défauts est uniforme dans la couche proche de la surface. D'après les données de microscopie électronique à transmission (MET) (Fig. 4, voir également la Fig. 1 dans la réf. [9] et la Fig. 2 dans la réf. [26]), la forme de КTaO₃ et KNbO₃ les nanoparticules peuvent être modélisées par un cube. La distribution granulométrique des cristallites dans chaque composé obtenue à partir des données MET est présentée sur la figure 5.

Image TEM du KTaO₃ nanoparticules

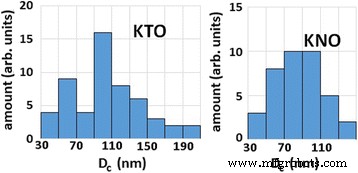
La distribution de taille des cristallites dans KTaO₃ et KNbO₃

Sur la base des courbes d'aimantation obtenues expérimentalement, en tenant compte notamment des nombres donnés de V(O) et de Fe (voir Tableau 1), nous remarquons le rôle dominant des lacunes d'oxygène dans l'aimantation. Dans cette hypothèse, une interaction d'échange peut être initiée par des électrons piégés dans des lacunes d'oxygène et médiée par des impuretés magnétiques ions Fe. Une telle interaction a été considérée dans le modèle des polarons magnétiques liés. Ce modèle a d'abord été proposé par les auteurs de [22] pour décrire l'apparition du ferromagnétisme dans les semi-conducteurs magnétiques dilués. Schématiquement, notre modèle est présenté sur la figure 6.

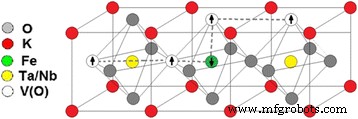
Modèle d'ordre magnétique à longue distance entre des électrons piégés dans des lacunes d'oxygène dans le KTaO₃ non stoechiométrique /KNbO₃ composé

Modélisation théorique dans l'approche de percolation

Pour déterminer la concentration critique de défauts totaux, pouvant conduire à la formation de polarons magnétiques, nous utilisons une approche de percolation. En utilisant les critères de la théorie de la percolation, il a été montré dans le travail [17] comment le seuil de percolation de l'ordre magnétique à longue distance est établi mathématiquement. En omettant les détails des approches et des principes de la réf. [17], nous allons nous concentrer sur les caractéristiques utilisées dans nos calculs et décrire le déroulement général du calcul.

Conformément aux données TEM (voir Fig. 4), considéré KTaO₃ et KNbO₃ les nanoparticules peuvent être modélisées par un cube. Le réseau cubique avec une constante de réseau de 0,4 nm a été utilisé. Dans la couche proche de la surface de 2 nm d'épaisseur (soit 5 cellules unitaires) (le contexte est donné ci-dessus, voir également les références [24] et [25]) avec des défauts distribués aléatoirement, des atomes de Fe et des lacunes d'oxygène V(O), en tenant compte du fait que la distribution des atomes de fer est uniforme. D'après les modèles de centres axiaux et rhombiques (voir Fig. 1), la présence d'atome de Fe au centre de la maille élémentaire (lorsqu'il se substitue aux atomes de Nb ou de Ta dans le KTaO₃ ou KNbO₃ treillis) s'accompagne de l'apparition de V(O) sur le(s) bord(s) de la cellule. Avec une certaine probabilité, une lacune d'oxygène V(O) ou deux lacunes 2 V(O) peuvent se produire. La probabilité est de 50% dans notre cas ce qui correspond au rapport déterminé expérimentalement des centres axial (Fe-V(O)) et rhombique (Fe-2 V(O)) dans KTaO₃ et KNbO₃ [9, 10, 15]. Les défauts ont été modélisés par des sphères dans nos calculs, à ce que les rayons de l'ion fer et de la lacune d'oxygène sont r (Fe ³⁺ ) = 0,064 nm et r (V(O)) = 0,132 nm, respectivement. La distance d entre les défauts a été défini comme la distance entre la surface des sphères et non entre leurs centres. Connaissant les coordonnées des défauts aléatoires, à savoir les atomes de Fe et les lacunes V(O), on calcule la distance d entre eux. Le résultat de la répartition des défauts est représenté schématiquement sur la figure 7.

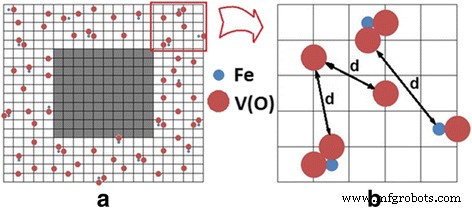
Répartition des défauts dans la couche superficielle. un Zone claire affiche la couche de défaut sous la surface. Zone grise reflète la profondeur des nanoparticules, où les défauts sont presque absents par rapport à la couche souterraine. La proportionnalité entre la taille de la zone de défaut sous la surface et le noyau interne sans défaut est brisée sur cette figure pour une représentation plus claire de la distribution des défauts dans la couche sous la surface. Les atomes de Fe sont répartis uniformément dans la profondeur de la couche de défaut, les lacunes d'oxygène V(O) sont situées à proximité des atomes de Fe. b Zoom de la couche défectueuse (a ); d est la distance entre les défauts

Selon la théorie de la percolation, l'ordre magnétique à longue distance dans le système se produit dès que l'amas infini se forme (voir, par exemple, p.235 dans la référence [17]). La distance entre les défauts, qui forment un amas infini, et remplissent donc la condition de percolation (« seuil de percolation »), est définie comme un rayon de percolation, R _pourcentage . Pour déterminer le rayon de percolation, le calcul a été effectué pour des nanoparticules de différentes tailles, afin de s'assurer que la condition de percolation est bien remplie. Pour le cas, le rapport entre le nombre de défauts magnétiques dans l'amas infini et le nombre total de défauts magnétiques dans le système reste inchangé dans les particules de différentes tailles. La taille des nanoparticules est D × D × D cellules unitaires, où D = 20, 30, 40. Pour déterminer la dépendance du rayon de percolation sur la concentration de défauts magnétiques, les calculs ont été effectués pour les concentrations présentées dans le tableau 2. Ici, n ₁ définit la concentration des lacunes d'oxygène qui ne sont pas situées à proximité des atomes de Fe, n ₂ est la concentration d'atomes de Fe, et n est une concentration totale de défauts. Notez que nous effectuons des calculs pour deux cas. Pour le cas I, n ₁ /n ₂ = const et n varie. Pour le cas II, n ₂ = const et n ₁ varie.

Afin de déterminer le rayon de percolation R _pourcentage , nous utilisons la procédure suivante. Pour chaque concentration, nous fixons une certaine valeur R qui variait de 0,1 à 5,9 nm avec un incrément de 0,2 nm. La distance d entre les défauts a été comparée à la valeur R (pour chaque R valeur). Ainsi, tous les défauts magnétiques sont divisés en deux groupes. Si la distance d _ij entre le i le plus proche e et j e défauts est inférieur ou égal au R , c'est-à-dire, d _ij ≤ R , nous classons ces défauts dans un groupe, dans lequel il existe un couplage magnétique entre les défauts ; sinon, si d _ij > R , nous renvoyons ces défauts à l'autre groupe, où le couplage entre défauts est absent (c'est-à-dire rompu). A la suite du calcul, on obtient la matrice de m × m , quels éléments sont des valeurs booléennes 1/0 (présence/absence de couplage entre les i e et j e défauts). Ici, m est le nombre de défauts dans la sous-surface de la particule d'une certaine taille. Ensuite, en utilisant le principe des chaînes de Markov, on trouve les amas magnétiques (c'est-à-dire les agrégats de points {Fe, V (O)}), qui interagissent indirectement. À cette fin, nous avons soulevé le m susmentionné × m matrice à la puissance m et obtenez une nouvelle matrice m × m , quels éléments sont des valeurs booléennes 1/0 (présence/absence d'interaction médiatisée entre les i e et j e défauts). La somme maximale de la ligne matricielle correspond à la taille du plus grand amas pour une taille de particule donnée. Des calculs similaires ont été effectués pour chaque valeur de R et la taille des nanoparticules. Résultats obtenus pour une concentration n = 0.6117 nm ⁻³ sont répertoriés dans le tableau 3. La zone en italique dans le tableau correspond au R = R _pourcentage valeur qui est le rayon de percolation R _pourcentage = 1,7 nm. Rayon de percolation R _pourcentage a été trouvé conformément au seuil de percolation décrit ci-dessus.

La figure 8 montre schématiquement la formation de l'amas infini dans les particules de différentes tailles.

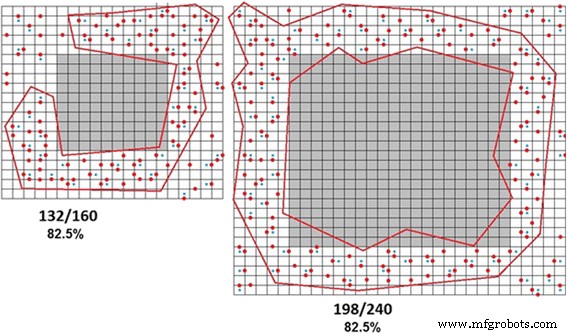
Formation d'amas infinis dans les particules de différentes tailles. Le seuil de percolation est de 82,5%, défini comme le pourcentage de défauts dans le cluster ne dépend pas de la taille des particules, comme prévu

Résultats et discussion

La figure 9a montre la dépendance du rayon de percolation R _pourcentage sur la concentration des défauts pour le cas I, c'est-à-dire lorsque n ₁ /n ₂ = const et n varie. Les courbes pleines sont tracées à l'aide de la formule

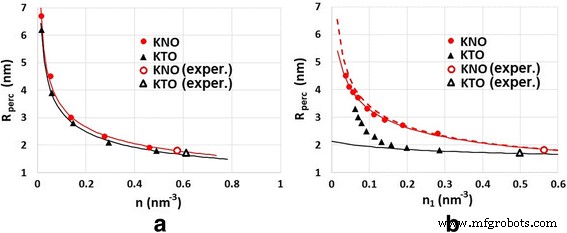
Rayon de percolation versus concentration de défauts pour deux cas :a n ₁ /n ₂ = const, n varie et b n ₂ = const, n ₁ varie. Les points sont calculés numériquement dans le cadre de notre modèle, les courbes pleines sont basées sur la formule (1). Les points marqués d'étiquettes correspondent aux matériaux étudiés (KTaO₃ et KNbO₃ )

avec les paramètres a = 1.6 et 1.7 pour KTO et KNO, respectivement, et b = 0,25 nm pour les deux, KTO et KNO. Le premier terme de la formule (3) est cohérent avec l'équation (4) de la réf. [20] pour un rayon de percolation, \( {R}_{\mathrm{perc}}=\frac{a}{\sqrt[3]{n}}. \)

La valeur de R _pourcentage est une certaine valeur critique, pour R> R _pourcentage , l'amas infini se formera, ce qui est dans la condition nécessaire de l'apparition de l'ordre magnétique à longue distance dans le cadre de la théorie de la percolation. Nous avons supposé que le rayon R _pourcentage est le même pour les couples Fe-Fe, V(O)-V(O) et V(O)-Fe. Cependant, sur la base des résultats calculés et des faits expérimentaux, nous pouvons affirmer que le rayon R _pourcentage ne peut pas être inférieur à 1,6 nm pour KTaO₃ et 1,7 nm pour KNbO₃ .

Considérons la formule (3) plus en détail. La signification physique de l'expression \( 1/\sqrt[3]{n} \) est la distance entre les défauts participant à l'échange magnétique pour l'apparition d'un ordre à longue distance. La valeur a peut être à la fois inférieur et supérieur à 1. Lorsque le rayon R _pourcentage correspond à la distance moyenne entre défauts, la valeur a = 1, et donc \( {R}_{\mathrm{perc}}=1/\sqrt[3]{n} \). Lorsque le nombre de couplages magnétiques aléatoires, qui sont formés par l'interaction entre des défauts à une distance inférieure à la moyenne, est suffisant pour la formation d'amas infini, la valeur a est inférieur à 1. Par exemple, a = 0,86 dans le travail [17]. Il s'avère que le R _pourcentage est 1,6 à 1,7 fois supérieure à la distance moyenne entre les défauts dans notre cas. Cela peut être expliqué comme suit.

La valeur de la distance moyenne entre les défauts est logique pour une répartition uniforme des défauts dans la couche souterraine. La distribution des atomes de Fe est considérée comme quasi-uniforme, mais compte tenu du fait que les atomes de Fe sont placés au centre de la cellule, leurs positions sont des coordonnées spatiales discrètes, ce qui affecte également la valeur a dans l'Eq.3, et l'emplacement des lacunes d'oxygène V(O) n'est pas uniforme car il s'agit toujours d'atomes de Fe proches (voir Fig. 6). Ainsi, la distance entre les atomes de Fe est beaucoup plus grande que la distance entre l'atome de Fe et la lacune d'oxygène V(O). Par conséquent, le rayon R _pourcentage en fait ne dépend pas de la distance moyenne entre tous les défauts, mais cela dépend de la distance moyenne entre les défauts dans différentes cellules unitaires (cela peut être la distance entre le Fe-Fe, V(O)-V(O), V(O )-Fe). La présence de lacunes d'oxygène à proximité des atomes de Fe réduit légèrement la distance entre les cellules défectueuses en raison de la faible distance V(O)-Fe par rapport à la distance Fe-Fe. Cela signifie que dans ce cas, nous avons en fait affaire à la distance moyenne entre les atomes de Fe.

Soustraction de la deuxième composante b = 0,25 nm dans l'équation (3) peut être expliqué comme suit. Typiquement, la distance entre les défauts dans cette équation est définie comme la distance entre les centres des défauts, si un défaut est simulé comme un point. Dans nos calculs, R _pourcentage est défini comme la distance entre les surfaces de la sphère dans laquelle on a placé le(s) défaut(s). Donc, la valeur R_perc , estimé comme la distance entre les surfaces des sphères, est différent du R _pourcentage estimée comme la distance entre les centres au moins sur la somme de deux rayons de défauts en interaction. La somme peut varier de 0,128 nm pour l'interaction Fe-Fe (Fig. 10a) à 0,264 nm pour l'interaction V(O)-V(O) (Fig. 10c). De plus, comme la distance entre l'atome de Fe et la lacune la plus proche V(O) est très inférieure à celle calculée, nécessaire pour établir un couplage entre défauts, dans certains cas, R _pourcentage peut être défini comme la distance V(O)-Fe ou V(O)-V(O) de différentes cellules (voir Fig 10b, c). Lorsque le nombre de V(O) augmente, le nombre de cas présentés sur la figure 10b, c augmente également, respectivement. En conséquence, la valeur calculée de b = 0,25 nm indique que principalement une interaction d'échange se produit directement entre les électrons piégés dans les lacunes d'oxygène.

Réduction de R _pourcentage pour l'interaction entre les différents défauts (a -c ) en comparaison avec une distribution uniforme de Fe (bleu ) est causée par la présence de lacunes d'oxygène V(O) (rouge )

La figure 9b montre la dépendance du rayon de percolation R _pourcentage sur la concentration des défauts pour le cas II, c'est-à-dire lorsque n ₂ = const et n ₁ varie. Ici, l'influence des atomes de Fe devient plus grande à mesure que n ₁ diminue. Ceci est plus prononcé pour le KTO (courbe continue noire sur la figure 9b). Néanmoins, nous avons essayé d'ajuster les données calculées à l'aide de la formule (3) avec les paramètres a = 0.66 et b = 0.15 nm. La valeur de b indique que la quantité relative d'interactions directes V(O)-V(O) diminue, tandis que la quantité d'interactions indirectes via des atomes de Fe augmente.