Modélisation d'ADC à l'aide d'un polynôme d'intermodulation et d'un nombre effectif de bits

Dans cet article, nous discutons d'une autre méthodologie sur la façon de modéliser les ADC dans les simulations système, cette fois en utilisant le nombre effectif de bits et en ajustant également notre ADC en introduisant un polynôme d'ordre 5 à l'entrée de quantificateur idéale.

Jusqu'à présent dans cette série, nous avons discuté des avantages de différentes manières de modéliser des convertisseurs de données dans des simulations de système, en particulier en utilisant une méthode de modélisation utilisant le nombre effectif de bits ou ENOB.

Maintenant, nous allons continuer cette discussion en ajoutant un nouvel élément :ajuster notre modèle ADC directement avec un polynôme d'ordre 5 ajouté à l'entrée de quantificateur idéale.

Description de notre nouveau modèle ADC

Le modèle présenté dans notre article précédent n'a pas abouti à des fréquences parasites distinctes (spurs). Étant donné que les éperons sont une caractéristique importante des performances de l'ADC, un meilleur modèle était nécessaire.

Ceci est illustré à la figure 1.

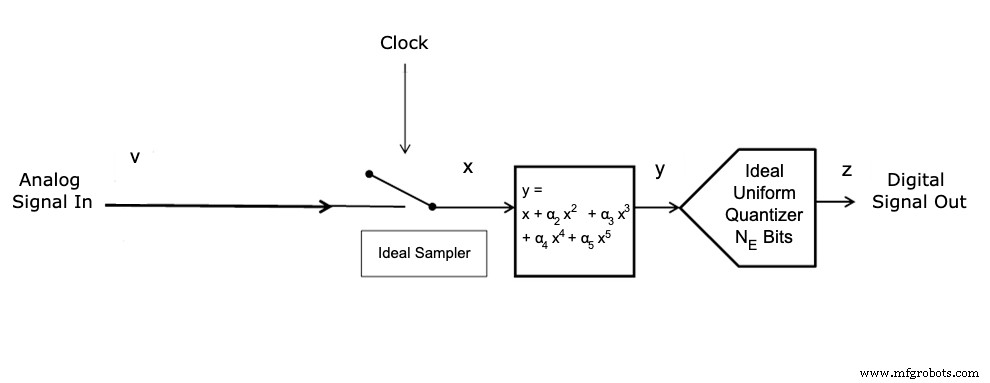
Figure 1.

Cela ajoute un polynôme d'ordre 5 à l'entrée de quantificateur idéale.

Une entrée bicolore doit être utilisée pour déterminer les paramètres α_i (f_c ) et N_E (f_c ); où f_c est la fréquence centrale entre les tons, comme le montre la figure 2 (que vous reconnaîtrez comme la figure 4 de notre premier article).

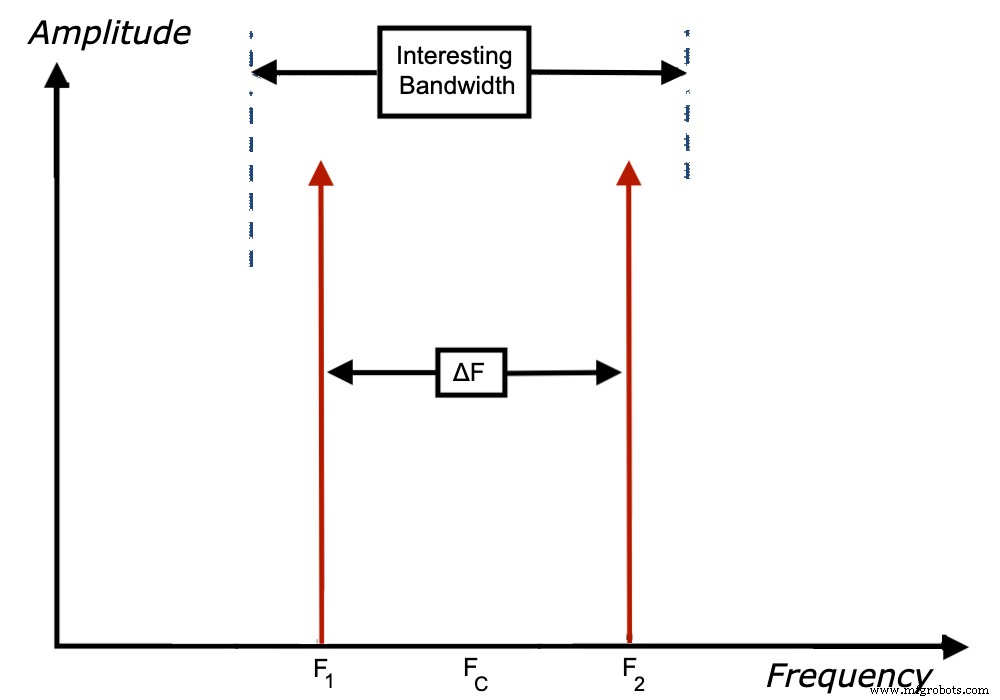
Figure 2.

Si l'un de ces paramètres est également fonction de Δf, la séparation entre les tons, il y a probablement une non-linéarité avec la mémoire dans l'ADC, et ce modèle ne s'appliquerait pas.

À titre d'exemple, la même entrée à deux tons que celle illustrée à la figure 3 (discutée comme la figure 3 de notre article précédent) a été utilisée, avec N_E =8 bits, ₃ =0,04, et tous les autres α_i =0. La même bande passante Nyquist (730,9 MHz) et la même « bande passante intéressante » (233,7 MHz) que dans notre article précédent existent.

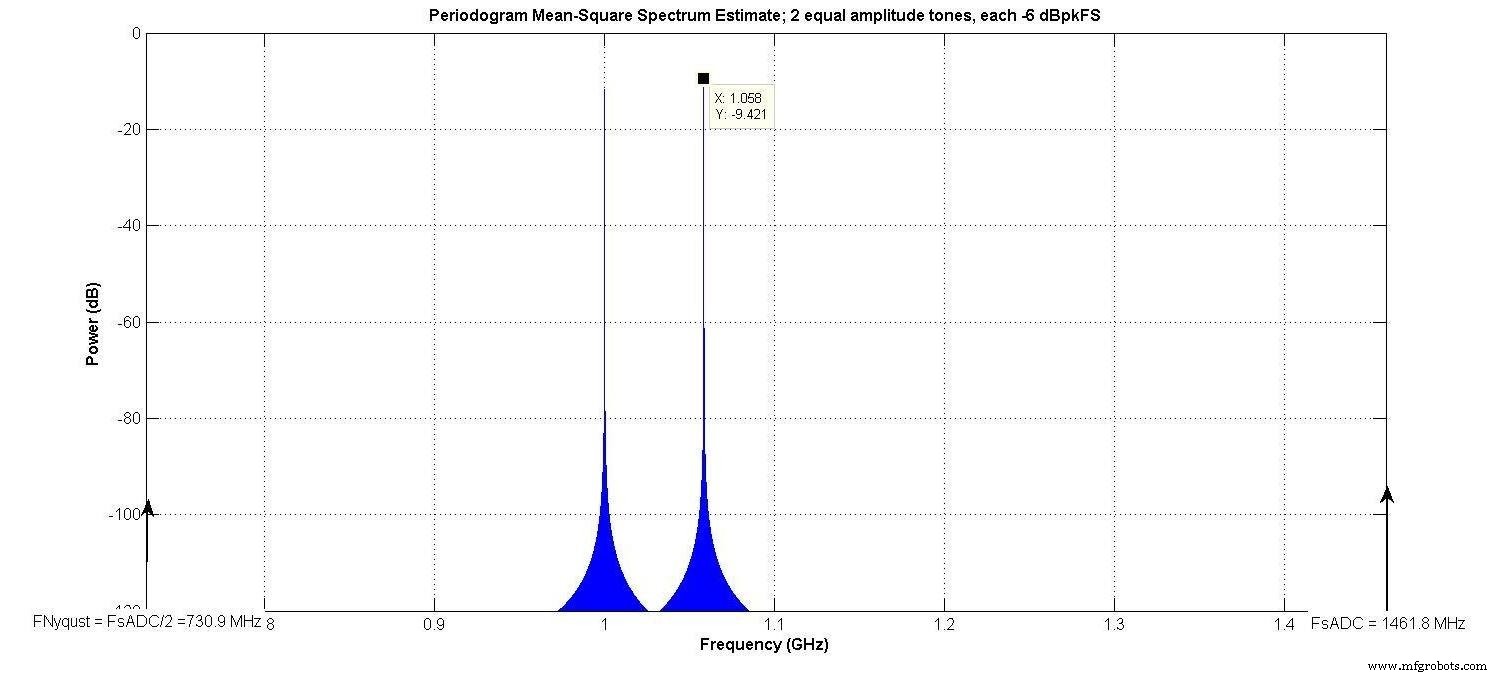
Figure 3.

La figure 4 montre la sortie avec une entrée à un ton et la figure 5 montre la sortie avec une entrée à deux tons.

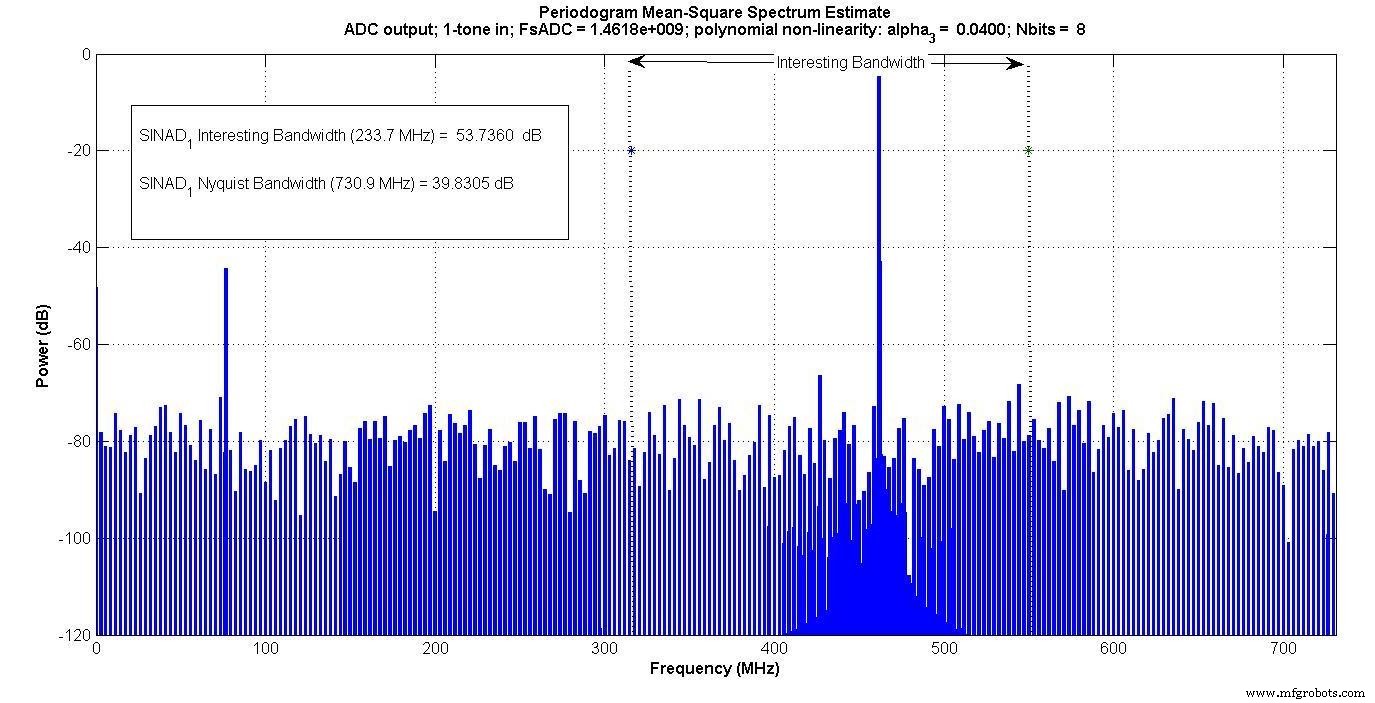
Figure 4.

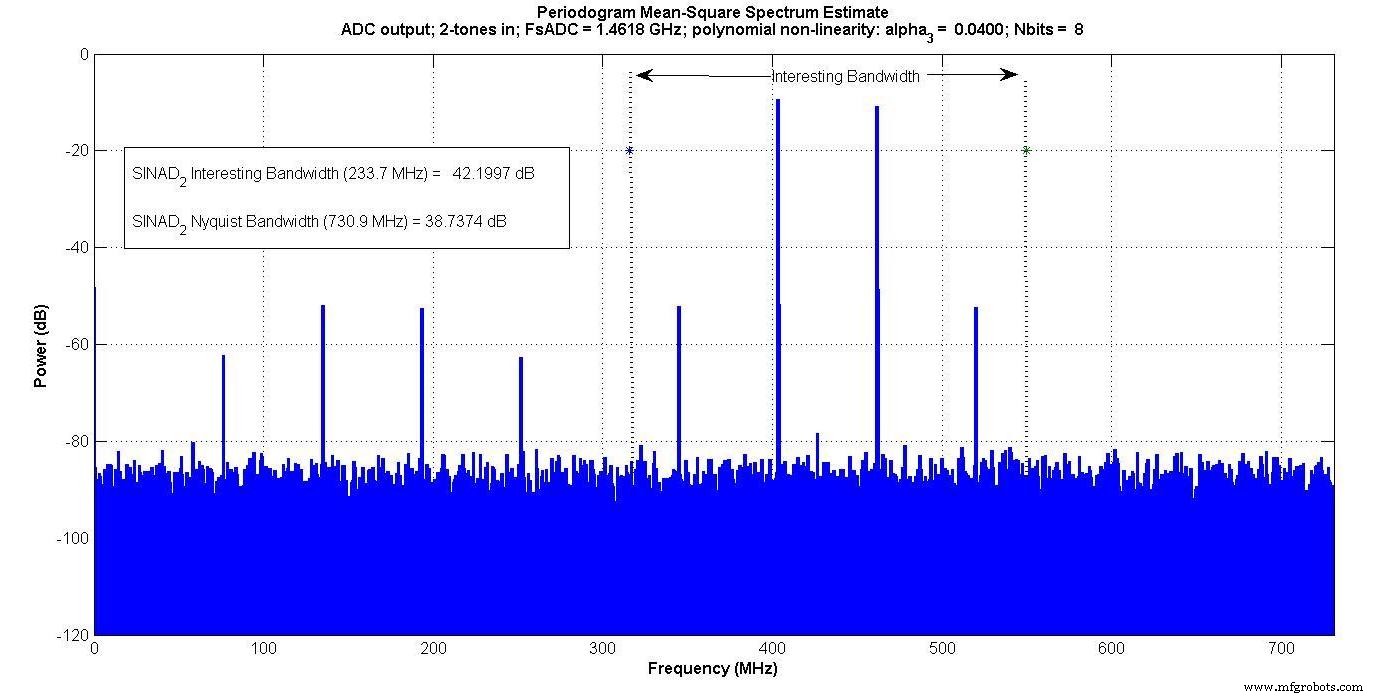
Figure 5.

Les produits d'intermodulation apparaissent à l'intérieur de la « bande passante intéressante » pour l'entrée bicolore, mais pas pour l'entrée monotone.

Si quelqu'un mesurait uniquement à l'intérieur de cette "bande passante intéressante" - par exemple, s'il y avait un filtre passe-bande numérique qui ne passait que cette bande - le test à un ton ne capturerait pas l'effet d'intermodulation, mais le test à deux tons le ferait.

La figure 6 trace les différents SINAD pour 5 à 12 bits d'entrée. Il est évident que l'entrée à un ton, mesurée dans la « bande passante intéressante », ne capture pas l'effet d'intermodulation sur plus de 7 bits.

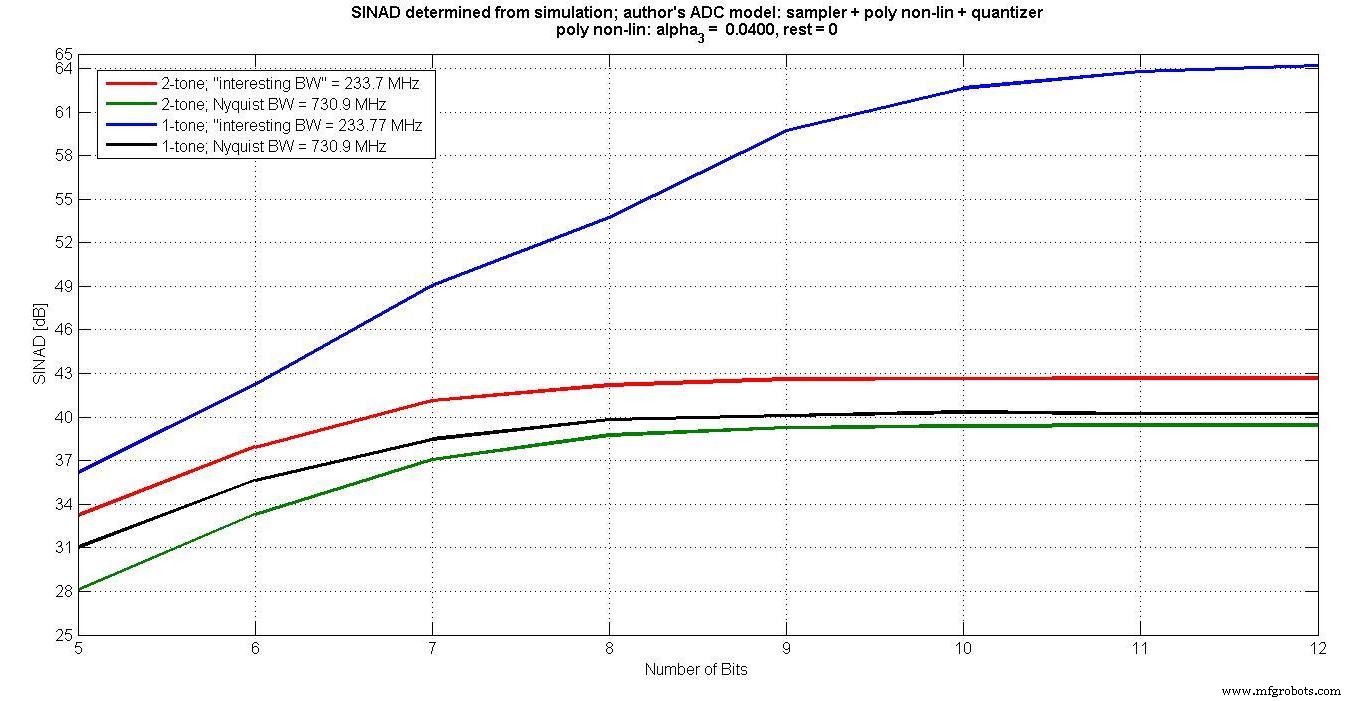
Figure 6.

Aussi, pour plus de 7 bits, puisque le bruit de quantification diminue à mesure que le nombre de bits augmente, mais que la distorsion d'intermodulation reste la même, le SINAD ne s'améliore pas avec plus de bits.

Comparaison avec le modèle des fabricants

Cher lecteur :Vous vous demandez peut-être maintenant; "Et alors? Ce ne sont que quelques modèles et leurs réponses à certains signaux. Quel est le but ?"

L'objectif devrait être que des mesures bicolores puissent être effectuées sur un CAN et que les valeurs des paramètres indiquées sur la figure 1 soient sélectionnées pour s'adapter au mieux à la sortie ADC mesurée. Cela peut souvent être fait en les ajustant manuellement jusqu'à ce qu'un bon ajustement soit obtenu. Ensuite, le modèle simplifié peut être utilisé dans des simulations de taux d'erreur sur les bits longs (BER).

Les mesures peuvent être effectuées sur un appareil réel, sur un bon modèle d'appareil ou être obtenues à partir des fiches techniques des fabricants.

Pour être un bon modèle, il doit se rapprocher étroitement de l'appareil réel ; comme un modèle SPICE complet. Un modèle aussi compliqué prendrait trop de temps à exécuter dans une simulation BER.

Ce qui était disponible pour votre auteur auprès d'un fabricant était ce qu'il appelait un modèle « comportemental », qui, selon eux, capturait tous les paramètres importants d'un modèle ADC particulier. Le modèle du fabricant a également pris en compte la gigue d'horloge interne et externe. Ceci a été utilisé pour évaluer la méthode.

Entrée à deux tons

La figure 7 montre la configuration de la simulation. L'entrée bicolore a été générée, puis entrée dans le modèle de votre auteur et du fabricant. Les deux ont été affichés avec une analyse spectrale.

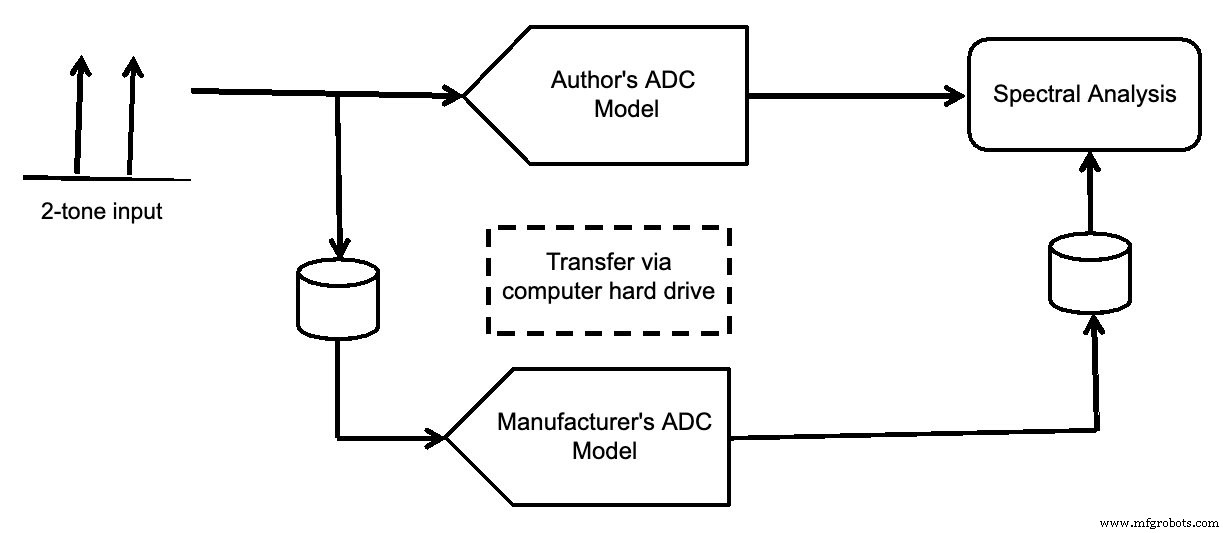
Figure 7.

La figure 8 montre l'entrée utilisée. Les deux tonalités sont comprises entre 300 et 350 MHz. La fréquence d'échantillonnage de l'ADC est d'environ 250 MHz, ces tonalités se trouvent donc dans la 3e zone de Nyquist.

Étant donné que chacun est à -6,02 dBpeakFS, lorsqu'ils s'ajoutent en phase, la tension sera deux fois plus élevée, ce qui donnera 0 dBpeakFS.

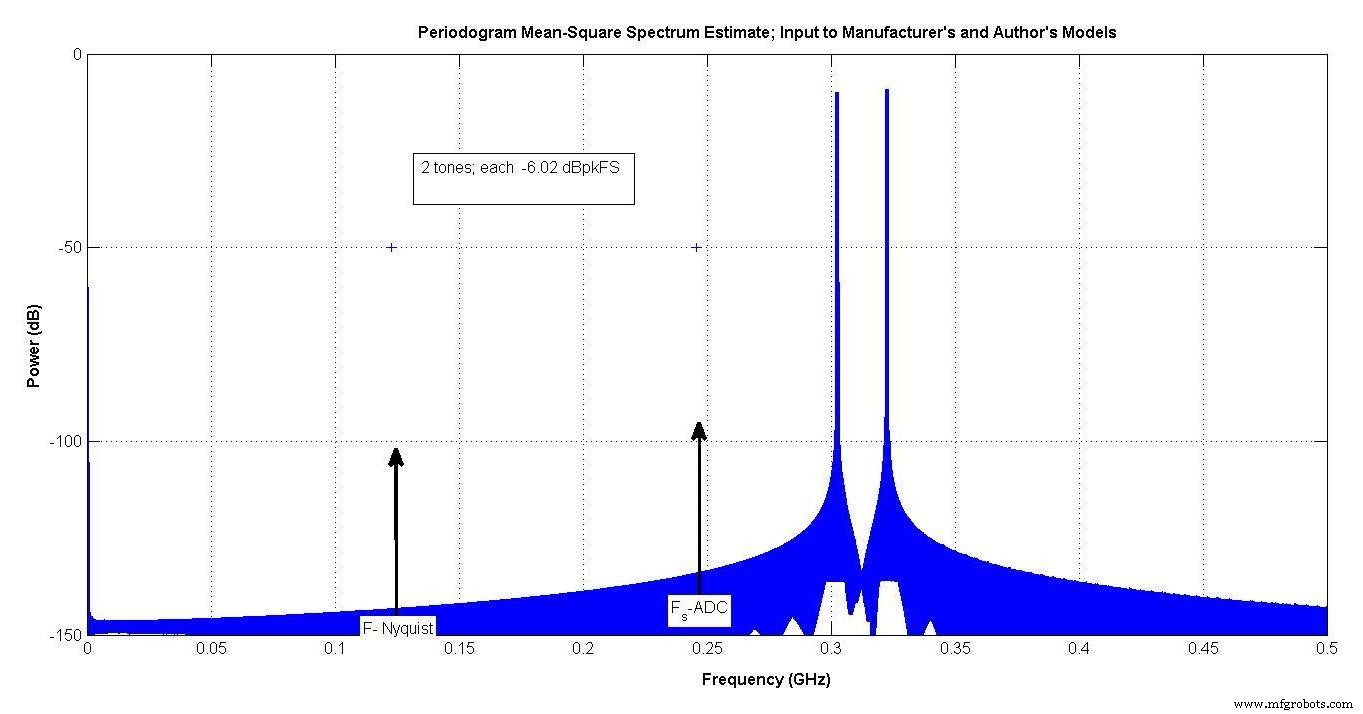
Figure 8.

La figure 9 montre la sortie du modèle du fabricant, qui avait un SINAD de 63,74 dB dans la « bande passante intéressante » d'environ 27 à 107 MHz.

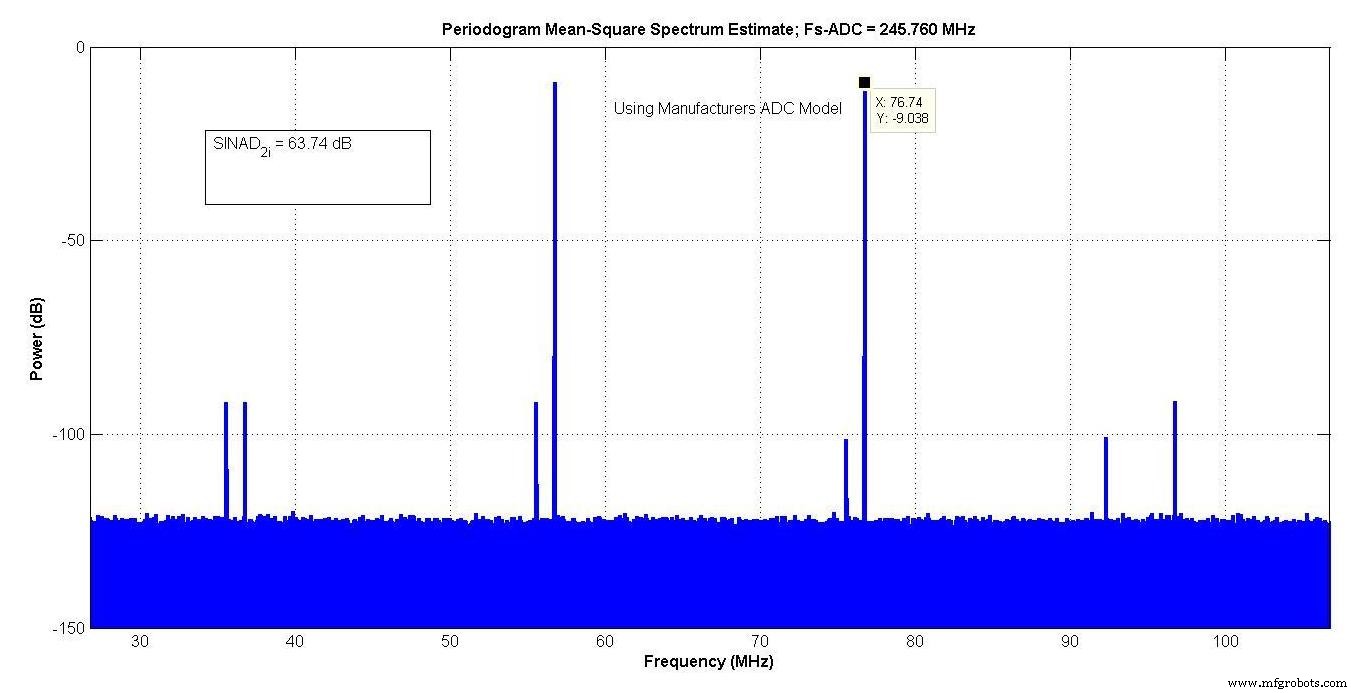
Figure 9.

La figure 10 montre le résultat après avoir ajusté les paramètres du modèle de votre auteur pour une correspondance.

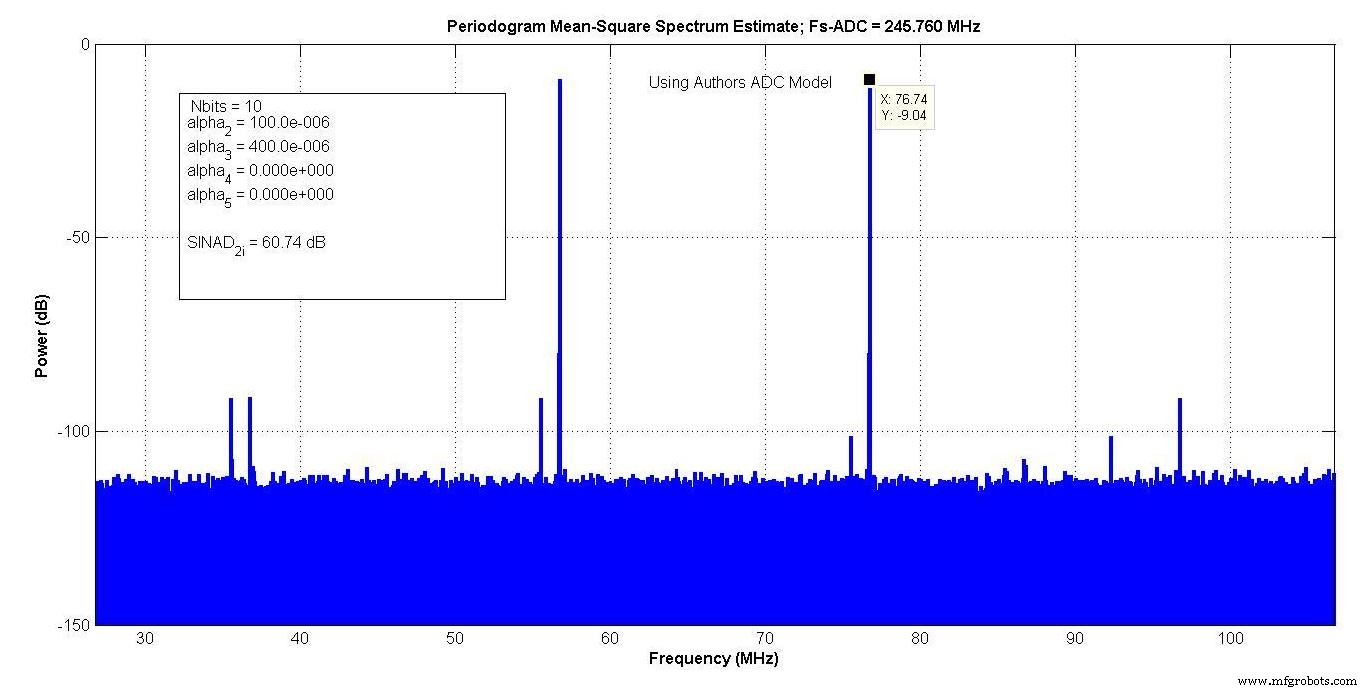
Figure 10.

Les coefficients polynomiaux donnaient suffisamment de degrés de liberté pour qu'une correspondance presque exacte puisse être faite avec les éperons. N_E de 11 bits a donné un bruit de fond inférieur de 3 dB au modèle du fabricant, et N_E de 10 bits lui donne 3 dB au dessus du modèle constructeur.

Votre auteur a décidé d'utiliser la valeur pessimiste de 10 bits, ce qui a donné un SINAD de 60,74 dB. Un modèle amélioré permettrait d'ajouter jusqu'à 6 dB de bruit blanc gaussien additif, donc la valeur la plus élevée de N_E pourrait être choisi, et le bruit supplémentaire ajouté pour correspondre aux planchers de bruit.

Entrée de forme d'onde OFDM

Les deux modèles peuvent maintenant être comparés avec une forme d'onde de communication comme entrée.

Un progiciel disponible dans le commerce est fourni avec un modèle LTE ; qui génère un signal OFDM. Le modèle comprend un modulateur, un canal d'évanouissement de Rayleigh sélectif en fréquence, un bruit gaussien blanc additif et un démodulateur.

Il est possible d'insérer les modèles ADC devant le démodulateur et d'évaluer le spectre de la sortie ADC et l'amplitude du vecteur d'erreur du signal OFDM, comme le montre la figure 11.

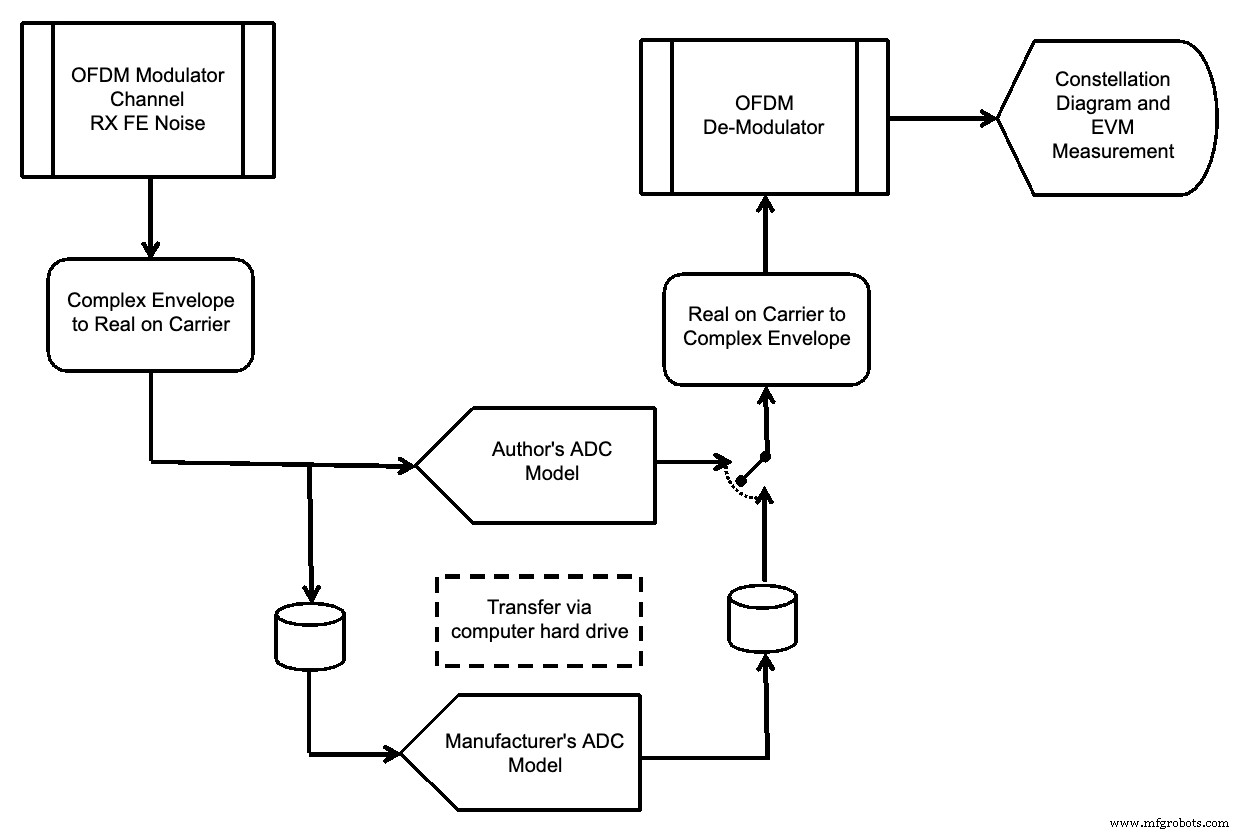
Figure 11.

Un signal OFDM qui avait des sous-porteuses 64-QAM a été utilisé. Les paramètres du modèle ADC de votre auteur sont les mêmes que ceux utilisés pour la figure 10.

Le progiciel disponible dans le commerce utilise une notation d'enveloppe complexe [3] pour former ses signaux. Cela permet uniquement de suivre les informations de modulation d'un échantillon à l'autre par des nombres complexes, et la fréquence porteuse simplement maintenue comme une constante connue. Ainsi, le nombre d'échantillons nécessaires pour décrire la forme d'onde est considérablement réduit.

Cependant, les entrées des modèles ADC doivent être un signal réel sur une porteuse explicite, pour prendre en compte la différence de performance ADC en fonction de la fréquence d'entrée. Ainsi, les transformations « Enveloppe complexe vers réel sur support » et « Réel sur support vers enveloppe complexe » [3] devaient être effectuées.

La figure 12 montre l'entrée du signal OFDM dans les deux modèles ADC. Il est centré sur la même fréquence que les deux tons illustrés à la figure 8.

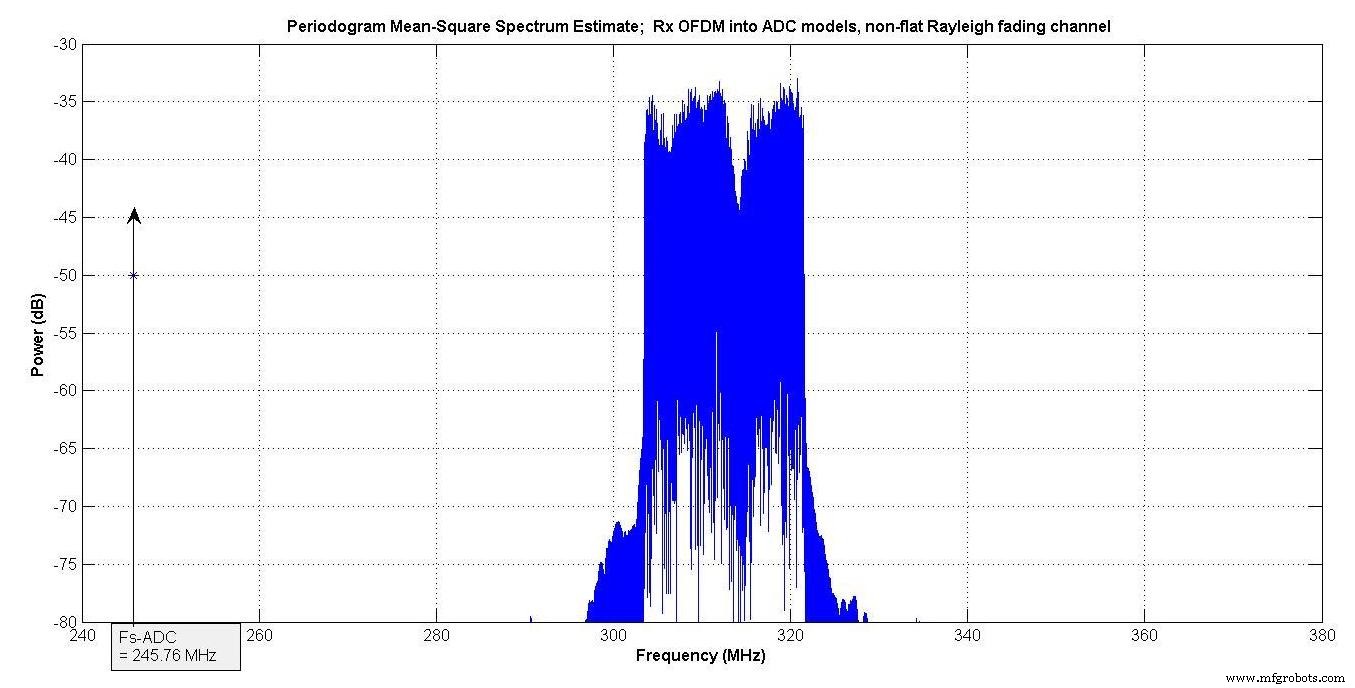
Figure 12.

Le niveau dBrmsFS dans les deux modèles ADC était de -7 dBrmsFS.

La figure 13 montre le spectre du modèle du fabricant et la figure 14 celui du modèle de votre auteur. Les deux montrent une repousse spectrale en raison de la non-linéarité des ADC. Les spectres sont très proches.

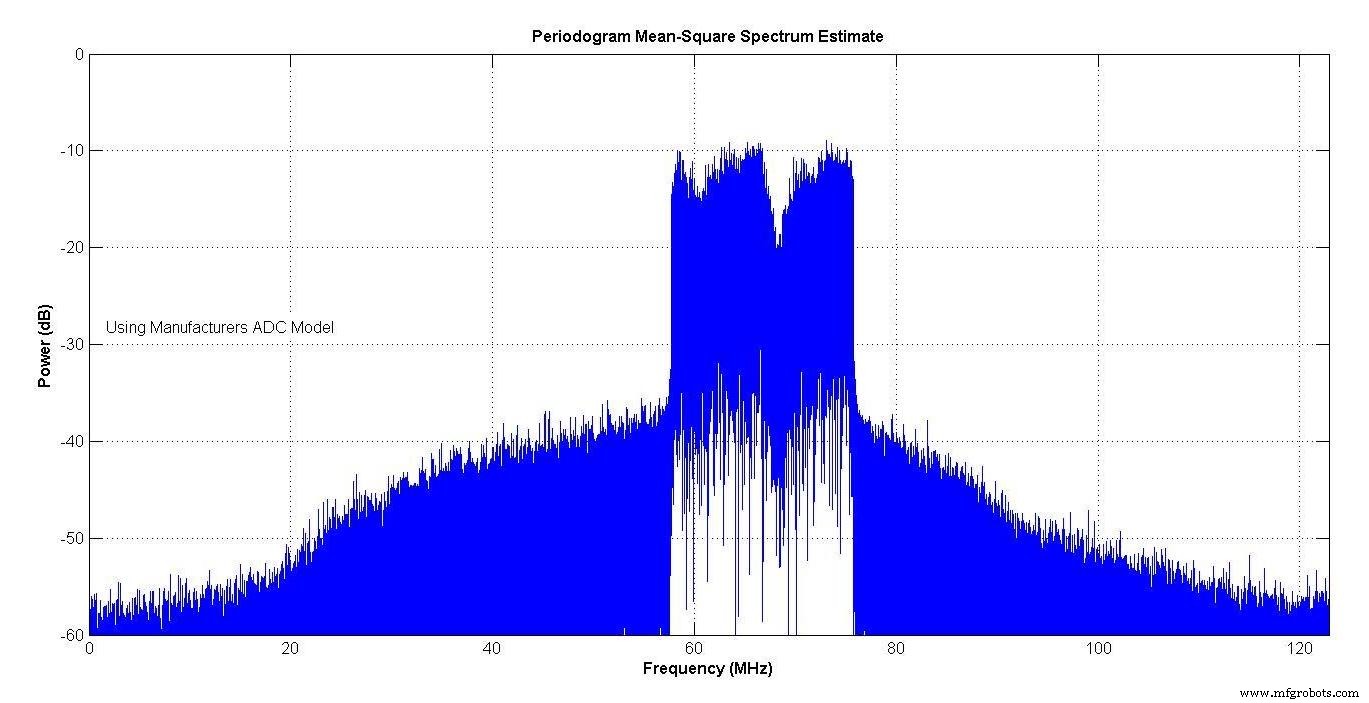
Figure 13.

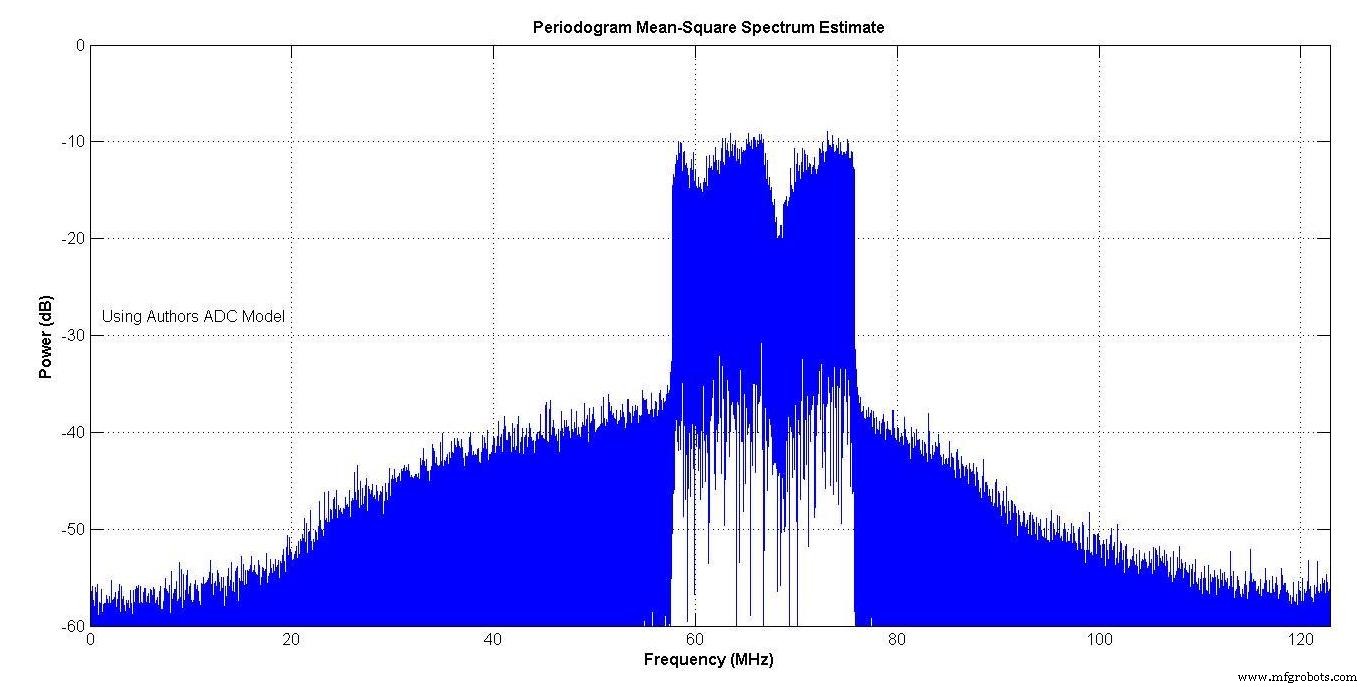
Figure 14.

La figure 15 montre la constellation de l'OFDM reçu pour le modèle du fabricant, et la figure 16 la montre pour le modèle de votre auteur.

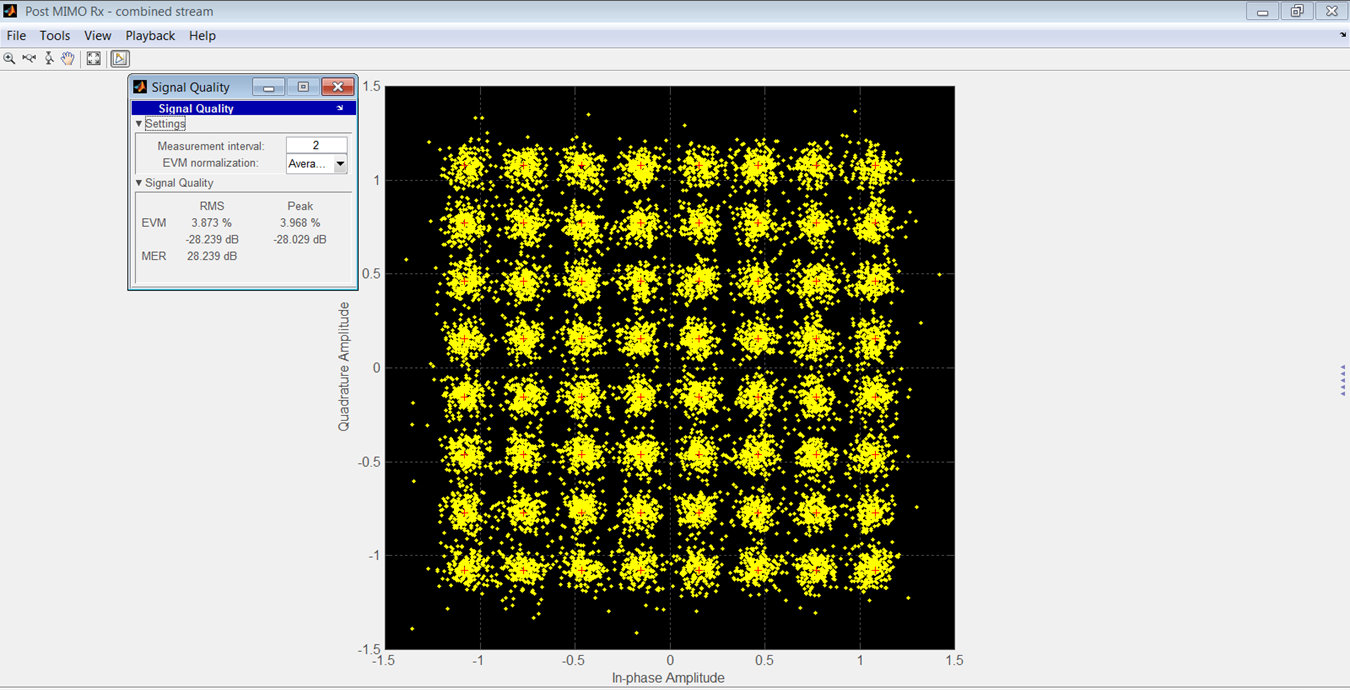
Figure 15.

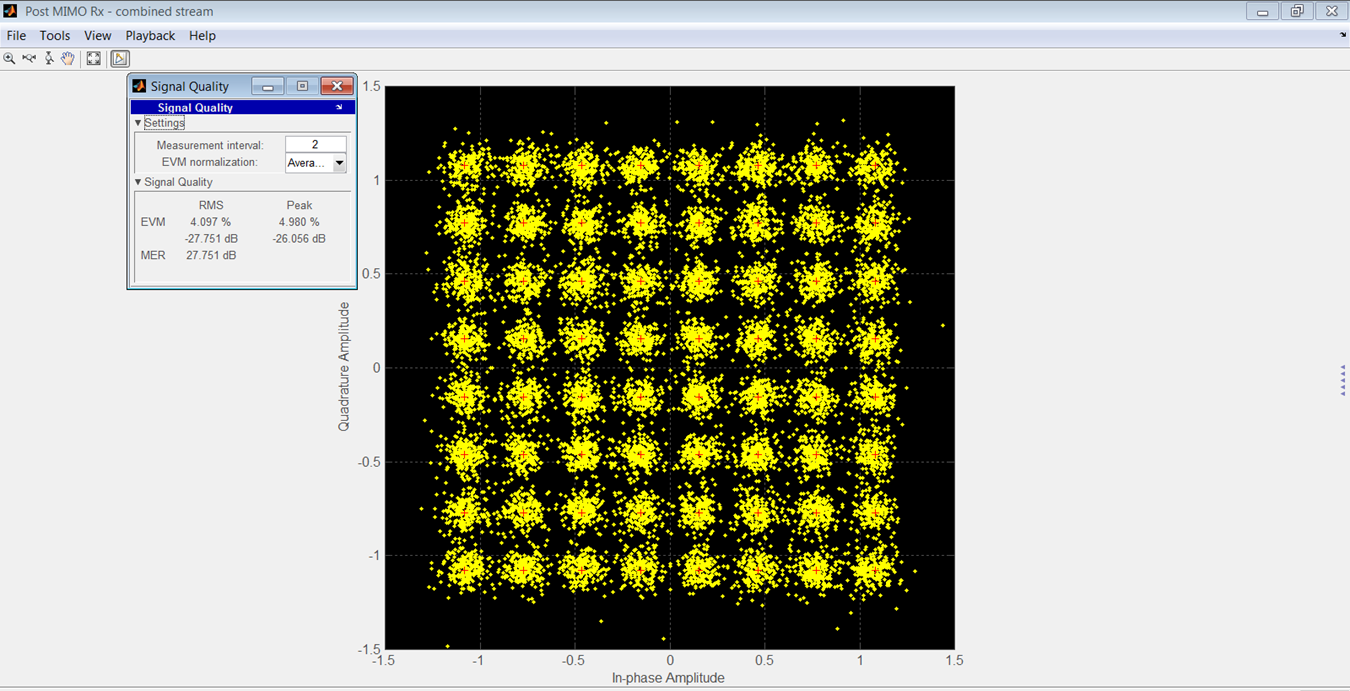
Figure 16.

Une comparaison des EVM efficaces et maximales se trouve dans le tableau 3. Le SNR était de 90 dB pour ces résultats.

Tableau 3.

Sur une plage de -7 à -47 dBrmsFS, la différence efficace entre les EVM des deux modèles était de 3,46 dB.

Globalement, le modèle de votre auteur donne des résultats très similaires à celui du constructeur, pour un ensemble de paramètres assez simple. Aucune information sur le modèle du fabricant n'était disponible, mais il peut être similaire à celui de votre auteur.

Dans tous les cas, les simulations se sont déroulées plus rapidement en utilisant le modèle de votre auteur, car il n'était pas nécessaire de transférer des données entre les logiciels de simulation. Ainsi, le modèle de votre auteur a été utilisé dans la simulation du taux d'erreur sur les bits (BER) illustrée à la figure 17.

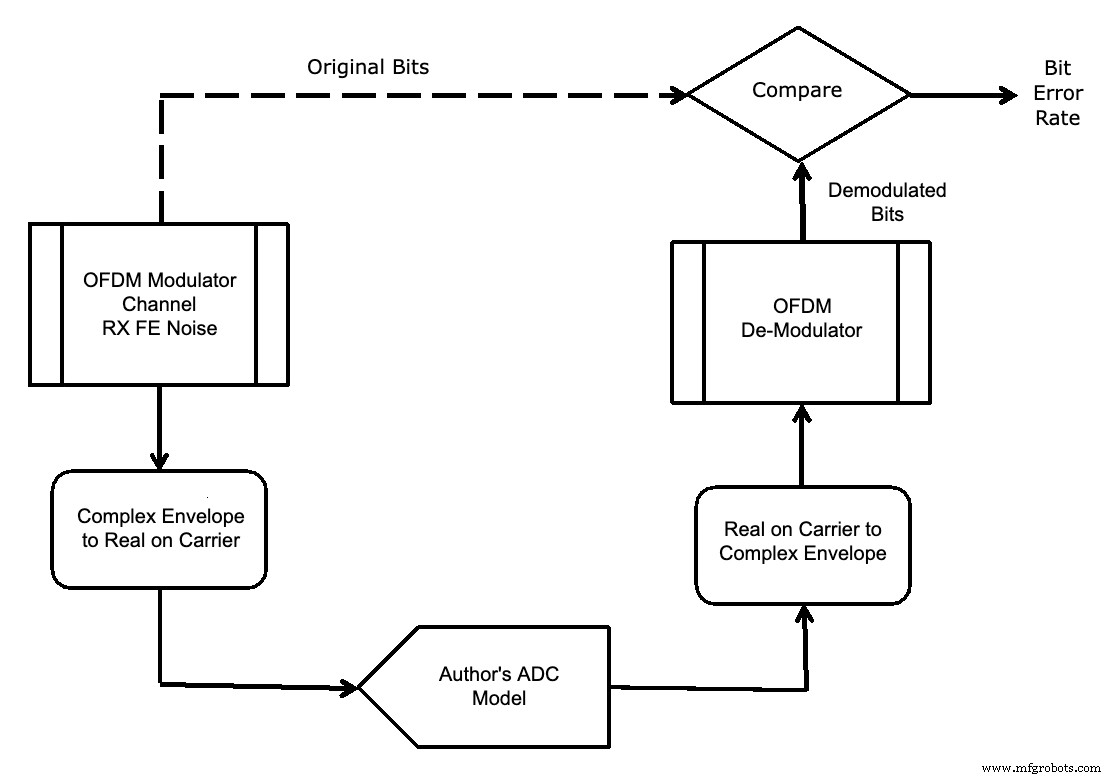
Figure 17.

Un paramètre important lors de la conception d'un système avec un CAN est le niveau optimal pour placer le signal par rapport à la pleine échelle du CAN.

Un niveau trop bas rend le signal trop faible par rapport au bruit et à la distorsion.

Un niveau trop élevé entraîne un écrêtage excessif, qui déforme également le signal. Habituellement, un niveau qui permet un certain écrêtage est optimal.

Le BER pour trois SNR différents et des niveaux de signal de -41 à -7 dBrmsFS est illustré à la Figure 18.

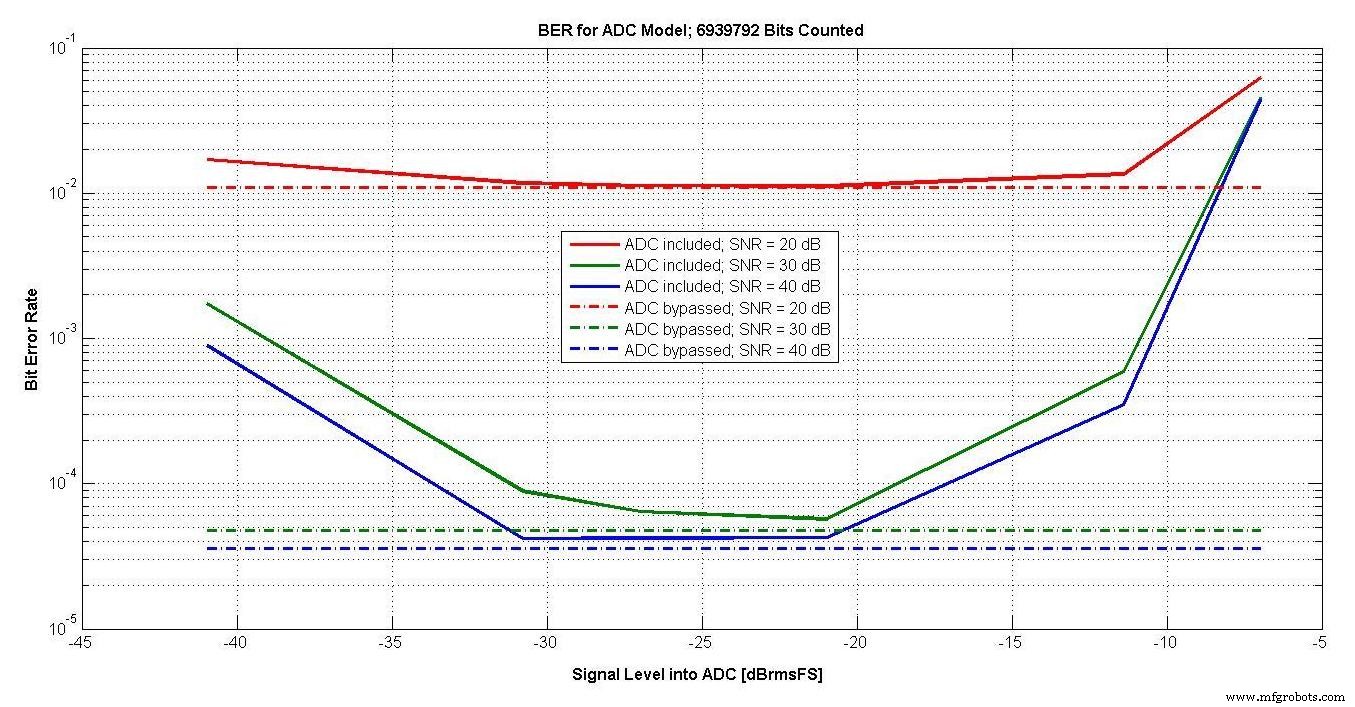
Figure 18.

Le BER est également indiqué avec les lignes en pointillés lorsque le modèle ADC est contourné. Avec l'ADC, il y a une plage d'environ 10 dB qui est optimale, et un contrôle de gain automatique devrait maintenir le signal dans cette plage.

---

Dans le prochain article, nous terminerons cette série en concluant par quelques réflexions sur un meilleur modèle à utiliser et nous parlerons également un peu des modèles pour DAC. Veuillez partager vos réflexions sur cette série dans les commentaires ci-dessous.