Calculatrice de règle de Cramer - Système à 2 et 3 équations

Règle et calculateur de Cramer pour l'analyse de circuits linéaires | Pas à pas avec des exemples résolus

Aujourd'hui, nous allons partager une autre technique d'analyse de circuit simple mais puissante connue sous le nom de "règle de Cramer ".

• Analyse de circuit SUPERMESH | Pas à pas avec un exemple résolu

Mise à jour : Nous avons ajouté le calculateur de règles de Cramer en ligne où vous pouvez résoudre un système à deux équations ainsi qu'un système à trois équations. Vérifiez le calculateur de règles de Cramer dans les deux sections du message. Merci

Vous trouverez ci-dessous le didacticiel étape par étape d'exemples résolus, qui explique comment résoudre un circuit électrique complexe et un réseau selon la règle de Cramer.

Calculateur de règle de Cramer pour 2×2 (Système à deux équations)

Exemple 2 : Utilisez l'analyse de maillage pour déterminer les trois courants de maillage dans le circuit ci-dessous. Utilisez la règle de Cramer pour simplifier.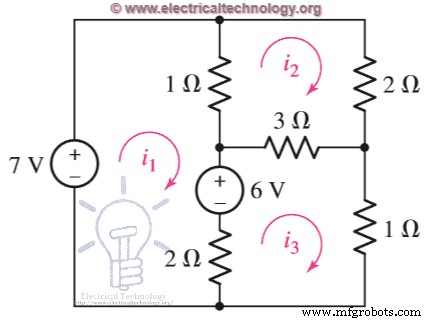 Tout d'abord, appliquez le KVL sur chaque mesh un par un, et écrivez ses équations. -7+1(je ₁ –je ₂ ) +6+2(je ₁ –je ₃ ) =0         1(je ₂ –je ₁ ) + 2i ₂ + 3(je ₂ –je ₃ ) =0      2(je ₃ –je ₁ ) – 6+3(je ₃ –je ₂ ) + 1je ₃ =0Simplifier,     3i ₁ –je ₂ – 2i ₃ =1                   … Eq….. (1)  – i ₁ + 6i ₂ – 3i ₃ =0                   … Éq….. (2) -2i ₁ – 3i ₂ + 6i ₃ =6                   … Eq….. (3) Maintenant, écrivez les équations ci-dessus sous la forme matricielle. 3je ₁ – je ₂ – 2i ₃ =1   –je ₁ + 6i ₂ – 3i ₃ =0-2i ₁ – 3i ₂ + 6i ₃ =6  Maintenant, nous allons trouver le déterminant du coefficient de ∆. Comment allons-nous faire cela? Vérifiez simplement la figure ci-dessous pour une meilleure explication. Cliquez sur l'image pour l'agrandir  L'étape complète est donc illustrée ci-dessous. ∆ =+3 (6 x 6) – (- 3 x –3) – (-1 (- 1 x 6)-(-2 x –3) + (-2 (-1 x –3) – (-2 x 6)∆ =81 -12 -30 =39 Maintenant, trouvez le ∆₁ de la même manière qu'expliqué ci-dessus. Mais, remplacez simplement la première colonne de la matrice par la "colonne de réponse". Pour plus de détails, consultez la figure ci-dessous. 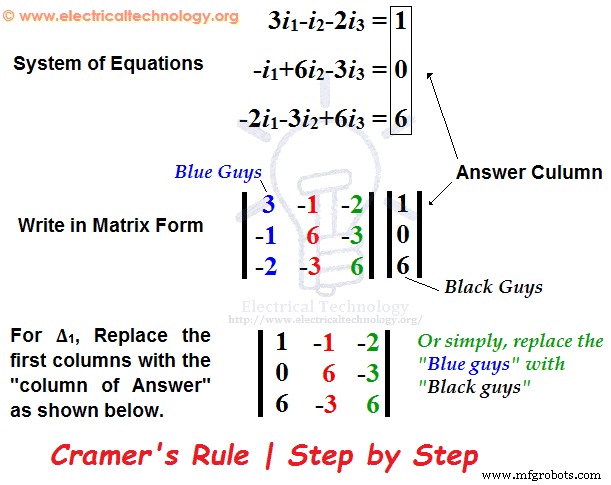Donc, voici l'étape complète pour trouver ∆₁ . Ici, nous avons remplacé les "Blue Guys" dans la première colonne par "Black Guys" :). 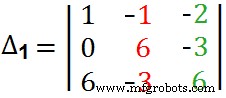=+1(36-9) – (–1[0+18]) –2(0- 36)=27 + 18 + 72∆₁ =117 Encore une fois, trouvez le ∆₂ avec la même méthode que celle expliquée précédemment. Remplacez simplement la deuxième colonne de la matrice par la "colonne de réponse", c'est-à-dire remplacez les "gars rouges" dans la colonne centrale par "les gars noirs" comme indiqué ci-dessous. 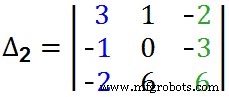=+3 (0 +18) -1[(-6)-(+6)] –2 (-6-0)=54+12+12 =78∆₂ =78 Enfin, trouvez le dernier ∆₃ . Remplacez simplement la troisième colonne par la "colonne de réponse", c'est-à-dire remplacez les "gars verts dans la troisième colonne par des "gars noirs" comme indiqué ci-dessous. =+3 (6 x 6) – (-3 x 0) – [-1(-1 x 6) – (-2 x 0)] + [1(-1) x (-3) – (-2) x (6)]=108 + 6 + 15∆₃ =117 Maintenant, résolvez et trouvez les valeurs inconnues de courant, c'est-à-dire i ₁ , je ₂ et je ₃ Comme le dit la règle de Cramer, les variables, c'est-à-dire i ₁ =∆1/∆₁ , je ₂ =∆/∆₂ et je ₃ =∆/∆₃ . Par conséquent, je ₁ =∆1/∆₁ =117/39i ₁ =3A Et je ₂ ,je ₂ ==∆/∆₂ =78/39je ₂ =2A Et enfin, je ₃ ;je ₃ =∆/∆₃ =117/39i ₃ =3A. J'espère que vous avez très bien compris la règle du Cramer et que vous avez apprécié le tutoriel étape par étape. S'il vous plaît, n'oubliez pas de partager avec vos amis. Entrez également votre adresse e-mail dans la case ci-dessous pour vous inscrire. Donc, nous vous enverrons plus de tutoriels comme celui ci-dessus. Merci.

Articles connexes et outils d'analyse de circuit :

• Théorème de Norton. Procédure facile étape par étape avec exemple (vues illustrées)
• Théorème de Thévenin. Procédure facile étape par étape avec exemple (vues illustrées)
• Calculatrices d'ingénierie électrique et électronique en ligne
• Plus de 10 outils de conception et de simulation en ligne pour les ingénieurs électriciens/électroniciens
• Conception de PCB :comment concevoir un PCB (étape par étape et vues illustrées)
• 15 applications Android incontournables pour les ingénieurs et les étudiants en électricité et en électronique
• Analyse de circuit SUPERNODE | Pas à pas avec un exemple résolu
• Analyse de circuit SUPERMESH | Pas à pas avec un exemple résolu
• Calculatrices de génie électrique et électronique