Impédance de surface des métasurfaces/structures hybrides en graphène

Résumé

La compréhension et la manipulation de l'impédance de surface dans la structure hybride du graphène est un problème important pour les applications de dispositifs optoélectroniques à base de graphène. Afin d'atteindre cet objectif dans la région térahertz, des expressions analytiques pour les impédances de la métasurface ont été dérivées, ce qui nous permet de comprendre facilement la relation entre les dimensions physiques et l'impédance. Les résultats de simulation montrent un excellent accord avec les prédictions analytiques. De plus, nous nous concentrons sur l'impédance synthétique lorsque patch carré et feuille de graphène sont réunis, discutons de l'influence de la taille de la métasurface ainsi que de la potentialité chimique du graphène sur l'impédance synthétique. Sur la base de ces résultats, un certain nombre d'absorbeurs ainsi que des dispositifs optiques peuvent être conçus qui utilisent des métasurfaces d'impédance.

Introduction

Ces dernières années, de nouvelles métasurfaces d'impédance artificielle, présentant des propriétés électromagnétiques anormales, ont été proposées et étudiées dans les littératures précédentes [1,2,3,4,5,6]. Pendant ce temps, de nombreux types d'applications de métasurface ont été introduits, tels que l'holographie [1], l'imagerie à haute résolution [2], la cape de tapis [3] et les absorbeurs [4, 5]. Les métasurfaces peuvent jouer un rôle important dans la réalisation des dispositifs optiques et térahertz minces. Néanmoins, en raison de la réponse dispersive des métasurfaces, de nombreux appareils ne peuvent fonctionner que dans une seule bande de fréquence et le spectre étroit ne peut pas être accordable. Très récemment, en faisant varier la tension appliquée à une large gamme de fréquences telles que les fréquences térahertz ou même optiques, la conductivité peut être contrôlée dynamiquement [7,8,9,10], c'est pourquoi le graphène a prouvé qu'il était le meilleur candidat pour le réglage. les caractéristiques des structures plasmoniques et métasurfaces [11]. Par conséquent, de nombreux dispositifs conçus par métasurface et graphène ont été proposés [12,13,14].

Entre-temps, plusieurs modèles analytiques pour calculer l'impédance équivalente des métasurfaces ou de la feuille de graphène ont été utilisés pour expliquer le mécanisme physique [8, 15, 16, 17, 18, 19, 20]. Ondes planes utilisées pour l'excitation de modèles de graphène ou de métasurfaces qui peuvent être divisés en deux méthodes différentes qui sont analytiques et informatiques. La méthode de calcul est un travail sur l'expression de Floquet [21, 22]. L'avantage d'utiliser cette méthode est qu'elle ne se limite pas à la géométrie des structures, et l'un des mérites les plus importants est qu'elle peut fournir des résultats précis. Néanmoins, les logiciels commerciaux utilisant cette méthode consomment un temps et des ressources de calcul considérables. D'autre part, une méthode analytique plus précise et précise est développée [23,24,25,26,27], elle est simple d'utilisation et permet une meilleure analyse des phénomènes physiques. Malgré les avantages mentionnés ci-dessus, les défis liés à la réalisation d'un modèle analytique de haute précision pour une unité de métasurface spécifique sont également importants. Heureusement, des efforts et des travaux considérables ont été faits pour prédire l'impédance de surface équivalente et ont produit de nombreux excellents résultats [16, 28]. Cependant, à la connaissance des auteurs, le modèle analytique capable de prédire l'impédance de surface de cette combinaison hybride n'est pas encore connu.

Dans cet article, un absorbeur artificiel 3D a été utilisé pour analyser et prédire l'impédance des structures hybrides métasurfaces/graphène, qui prend en compte la relation entre les métasurfaces et le graphène. Pour un calcul rapide de l'impédance de surface des métasurfaces, les formules analytiques ont d'abord été développées. Ces formules analytiques simples et précises peuvent permettre une élucidation complète et une exigence de base sur la conception d'impédance. Ensuite, les impédances des feuilles de graphène sont calculées. Enfin, nous nous concentrons sur la relation entre la taille de la métasurface, le potentiel chimique μ _c , et l'impédance de la structure composite. Ici, l'impédance de surface de la structure hybride métasurfaces/graphème est discutée en calculant ses composantes réelles et imaginaires. À notre connaissance, il n'y a presque pas de littérature rapportant ce mécanisme de manière exhaustive.

Méthodes

Impédances pour patchs carrés et feuilles de graphène

Une structure commune d'un absorbeur métasurface-graphène est présentée sur la figure 1a. Cet absorbeur à structure simple peut être facilement fabriqué par micro-usinage de surface. Dans cette configuration, une fine couche conductrice hybride métasurface-graphène et le plan de masse métallique sont séparés par un substrat diélectrique servant d'espaceur. La distance au sol est de h . Pour un carré de petite taille par rapport à la longueur d'onde (période du tableau D ≪ λ ) et les patchs sont séparés par des fentes étroites (largeur de la fente D − w ≪ D ), le modèle actuel est valide. Selon la théorie de la ligne de transmission, un modèle de circuit équivalent de la structure absorbante peut être construit (illustré sur la figure 1b), qui peut modéliser la métasurface-graphène. Une ligne de transmission, un court-circuit et l'impédance du réseau Z _mg , respectivement, modélisent la section du substrat diélectrique, le plan de masse et l'impédance de surface de la couche hybride à motifs supérieurs. Selon la théorie de la ligne de transmission, l'impédance d'entrée Z _dans de cet absorbeur peut être établi comme suit :

$$ \frac{1}{Z_{in}}=\frac{1}{Z_1}+\frac{1}{Z_{mg}}=\frac{1}{j{Z}_h\ast \tan \left({k}_{zh}h\right)}+\frac{1}{Z_{mg}} $$ (1)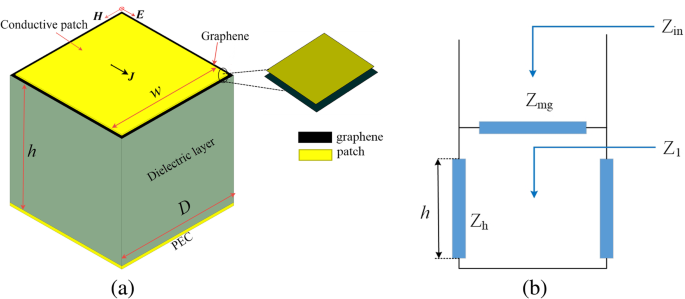

un Schéma de la cellule unitaire métasurface-absorbeur de graphène. b Modèle de circuit équivalent local

Où Z _h et k _zh sont respectivement l'impédance des couches de substrat et la constante de propagation dans cette région. Ensuite, l'absorptivité à l'incidence normale peut être calculée par

$$ A\left(\omega \right)=1-R\left(\omega \right)=1-{\left|{S}_{11}\right|}^2=1-{\left| \frac{Z_{in}-120\pi }{Z_{in}+120\pi}\right|}^2 $$ (2)

Il est évident que l'impédance de la feuille de métasurface-graphène peut être extraite du coefficient de réflexion simulé. La relation entre la taille du patch conducteur et le potentiel chimique μ _c peut être trouvé.

Impédance pour patchs carrés

Lorsque l'onde plane est perpendiculaire à la métasurface, le réseau de patchs planaires agit comme une grille capacitive (comme le montre la figure 1a). Impédance de surface Z _m peut être illustré comme les propriétés électromagnétiques des patchs carrés qui relient l'intensité moyenne du courant 〈J 〉 et l'intensité moyenne du champ électrique 〈E 〉 dans le plan de patch :

$$ \gauche\langle E\droit\rangle ={Z}_m\gauche\langle J\droit\rangle $$ (3)

Dans le cas d'une impédance de nappe résistive pure à pertes Z _s (im Z_s =0), à incidence normale l'impédance équivalente du patch est représentée par Z _m , et peut être exprimé comme suit [9, 18] :

$$ {Z}_m=\frac{D}{w}{Z}_s-j\frac{\eta_{eff}}{2\alpha } $$ (4)

Où $ {\eta}_{\mathrm{eff}=}\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_{\mathrm{eff}}} $ représente l'impédance d'onde de l'hôte uniforme moyen, et D /w est l'élément géométrique. La permittivité relative effective peut être approchée comme

$$ {\varepsilon}_{\mathrm{eff}}\approx \frac{\left({\varepsilon}_r+1\right)}{2} $$ (5)

De plus, le paramètre de grille α pour un réseau électriquement dense de patchs idéalement conducteurs peut être écrit comme

$$ \alpha =\frac{k_{\mathrm{eff}}D}{\pi}\ln \left(\frac{1}{\sin \frac{\pi w}{2D}}\right) $ $ (6)

$ {k}_{\mathrm{eff}}={k}_0\sqrt{\varepsilon_{\mathrm{eff}}} $ est le nombre d'onde dans le milieu hôte effectif. Dans l'espace libre, μ ₀ , ε ₀ , et k ₀ sont respectivement la perméabilité, la permittivité et le nombre d'onde. De plus, il convient de souligner que la relation (4) est valide lorsque la longueur d'onde λ est bien supérieur à D .

Selon l'équation (2), nous pouvons constater que l'impédance équivalente n'est pas seulement déterminée par la résistivité de la feuille de matériau, mais également par la période du réseau D et largeur w des paramètres de structure. Pour vérifier la certitude de telles formules analytiques, les résultats obtenus par des simulations en onde complète sont présentés et comparés aux solutions analytiques. La simulation discutée ici a été réalisée en utilisant le logiciel disponible dans le commerce Ansoft HFSS. Pour obtenir les caractéristiques de réflexion de la cellule unitaire métasurface-absorbeur de graphène, les conditions aux limites périodiques et les ports de Floquet ont été implémentés. Lors de sa simulation, l'impédance de nappe résistive pure avec Z _s = 35 Ω/sq est déposé sur le substrat avec une épaisseur h =20 m, longueur D =20 m, et la permittivité relative de ε _r = 3.2(1 − j 0,045). Afin d'extraire l'impédance de patch Z _m , selon la relation entre l'impédance d'entrée simulée Z _dans et l'impédance de surface de la dalle diélectrique mise à la terre Z _{g d} , l'impédance du patch de la métasurface peut être exprimée comme suit :

$$ {Z}_m=\frac{Z_{in}{Z}_{gd}}{Z_{gd}-{Z}_{in}} $$ (7)

Où Z _gd = jZ _d bronzage(k _d h ), $ {Z}_d=\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_r} $ est l'impédance caractéristique de la dalle, $ {k}_d=\omega \sqrt{\mu_0 {\varepsilon}_0{\varepsilon}_r} $ est la constante de propagation orthogonale à la surface du substrat pour le mode TEM.

Les résultats analytiques sont vérifiés par comparaison avec ceux simulés sur la base du coefficient de réflexion extrait, comme le montre la figure 2. Les courbes noires montrent les résultats simulés tandis que les courbes rouges sont calculées en utilisant l'expression analytique proposée. Bien qu'il existe une petite différence entre les résultats simulés et les prédictions théoriques, cela est dû à l'Eq. (3) est une équation approximative. La tendance générale est la même. Ainsi, confirmant la validité et l'exactitude de notre expression analytique pour ce modèle.

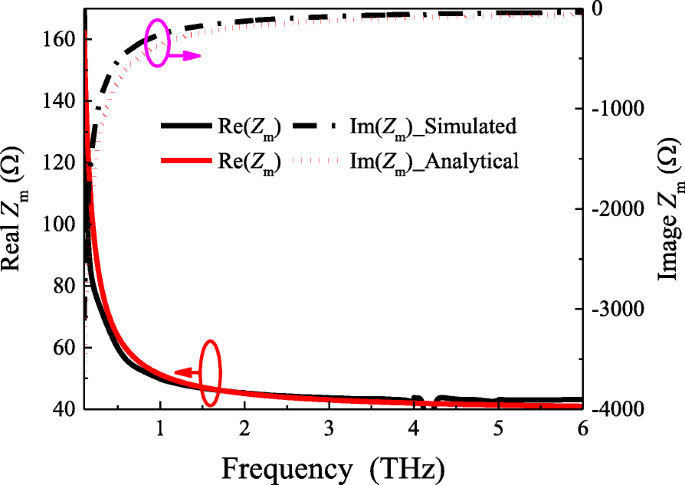
Impédances de grille simulées et analytiques du réseau de patchs avec w =19 µm

Afin d'étudier l'effet des tailles de patch sur l'impédance Z _m et valider l'efficacité de la formule (2), nous avons effectué la simulation numérique complémentaire. La figure 3 trace les parties réelles et imaginaires de l'impédance de grille Z _m pour divers paramètres géométriques de la maille élémentaire. A partir de la figure 3a, on peut observer que les parties réelles de l'impédance Z _m diminue à mesure que le paramètre w passe de 17 à 19,5 m. D'après l'équation 2, nous pouvons trouver que les parties réelles de Z _m sont inversement proportionnels à la longueur du patch w . Cependant, les parties imaginaires montrent la tendance inverse, comme indiqué en pointillés (illustré à la figure 3b). En tenant compte des Éqs. (2) et (3), les parties imaginaires peuvent être données par

$$ w\propto \ln \left(\mathit{\sin}\frac{\pi w}{2D}\right)\propto \frac{1}{\alpha}\propto \operatorname{Im}\left( {Z}_m\right) $$ (8)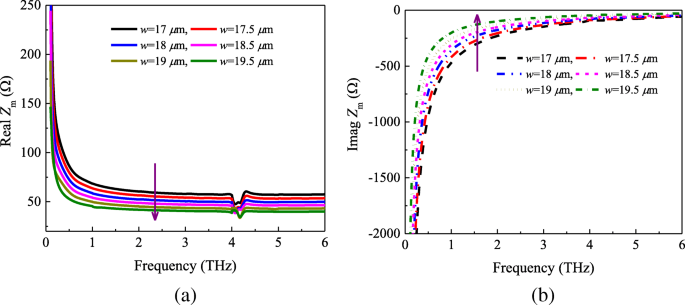

un Réel et b partie imaginaire de l'impédance Z _m avec différentes tailles de patch

De la relation (8), nous savons que lorsque w augmente de 17 à 19,5 m, les parties imaginaires de l'impédance Z _m augmentera.

Impédance pour les feuilles de graphène

Le graphène peut être vu comme une surface infiniment mince. Lorsqu'il n'y a pas de polarisation magnétostatique externe et de dispersion spatiale, la conductivité de surface σ _g , peut être calculé par [29]

$$ {\sigma}_{\mathrm{g}}=\frac{j{e}^2{k}_BT}{\pi {\mathrm{\hslash}}^2\left(\omega +j/ \tau \right)}\left[\frac{\mu_c}{k_BT}+2\ln \left({e}^{-{\mu}_c/{k}_BT}+1\right)\right] +\frac{j{e}^2}{4\pi \mathrm{\hslash}}\ln \left[\frac{2\left|{\mu}_c\right|-\left(\omega +j /\tau \right)\mathrm{\hslash}}{2\left|{\mu}_c\right|+\left(\omega +j/\tau \right)\mathrm{\hslash}}\right] $$ (9)

Où est la constante de Planck réduite, e est la charge d'un électron, k _B est la constante de Boltzmann, tandis que μ _c , ω , τ et T sont respectivement le potentiel chimique, la fréquence angulaire, le temps de relaxation et la température. Ici, nous supposons T =300 K et τ =0,1 ps tout au long de cette étude. L'impédance de feuille du graphène peut être calculée comme

$$ {Z}_g\left({\mu}_c\right)=1/{\sigma}_g={R}_g\left({\mu}_c\right)+j{X}_g\left( {\mu}_c\right) $$ (10)

Où R _g et X _g sont la résistance de surface et la réactance.

L'impédance de feuille de graphène est calculée selon les équations. (9) et (10). La figure 4 indique les composantes réelles et imaginaires de l'impédance de surface par rapport aux μ chimiques _c . Nous pouvons constater que la résistance de surface et la réactance diminuent continuellement avec l'augmentation de μ _c . De plus, les parties réelles de la résistance de surface de la feuille de graphène restent presque inchangées dans la plage de 0,2 à 6 THz lorsque le potentiel chimique est fixé à une certaine valeur.

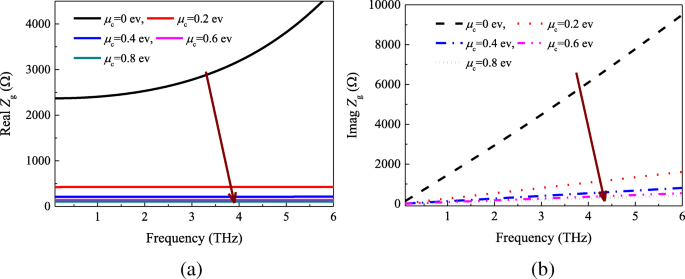
un Réel et b parties imaginaires de l'impédance de surface en fonction de la fréquence et du potentiel chimique

Résultats et discussion

Dans le cas d'un patch carré sur une feuille de graphène, l'impédance de surface pour cette structure hybride doit être déterminée. Dans les littératures antérieures [8, 30,31,32,33,34,35,36,37], l'impédance totale à la surface de cette structure hybride Z _mg est égal à la combinaison parallèle de l'impédance carrée Z _m et l'impédance de feuille de graphène Z _g , c'est-à-dire Z _mg = Z _m Z _g . Cependant, grâce à notre simulation et à nos calculs, il s'avère que cette relation n'est pas valide. Afin de vérifier l'authenticité, nous avons simulé une unité d'absorbeur métasurface-graphène montrée sur la figure 1a, puis récupéré l'impédance de surface du film selon l'équation (1). La figure 5 montre les valeurs analytiques et simulées de la partie réelle et imaginaire de Z _mg à différents potentiels chimiques avec w =19 µm.

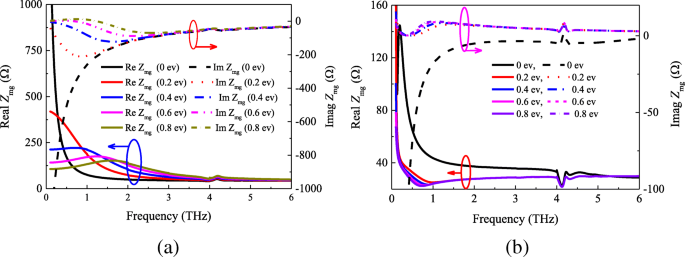
Impédance du film métasurface-graphene Z _mg avec des potentiels chimiques différents. un Analytique et b résultats simulés

A partir de la Fig. 5a, b, on peut voir qu'il existe de grandes différences entre les résultats analytiques et simulés. La figure 5a montre que la partie réelle des résultats analytiques était principalement concentrée entre 40 et 500 , et la partie imaginaire de l'impédance effective va de − 210 à 0 . Néanmoins, d'après la figure 5b, on peut trouver que les valeurs de la partie réelle de l'impédance de 20 à 140 Ω, et la partie imaginaire sont proches de 0 en augmentant μ _c de 0 à 0,8 ev. Cependant, les résultats analytiques et simulés montrent la même tendance que l'impédance aura tendance à être stable avec une fréquence croissante. La raison en est que les impédances de la feuille de graphène et du patch carré deviennent plus petites lorsque la fréquence augmente. Il est à noter que, par rapport à l'impédance du film métasurface-graphène à 0 ev avec les autres résultats, l'impédance Z _mg est bien différent. Cela est dû au fait que les valeurs de l'impédance de la feuille de graphène à 0 ev sont assez différentes du potentiel chimique plus élevé (vu sur la figure 4).

Ainsi, nous pouvons tirer les conclusions suivantes à partir de l'impédance calculée et simulée de la figure 5. Premièrement, l'impédance de surface du film de métasurface-graphène Z _mg n'est pas strictement égal à la combinaison parallèle de Z _m et Z _g . Cependant, deuxièmement, il existe une certaine relation entre eux. Afin de démontrer ces conclusions, nous simulons d'abord la structure de l'absorbeur montrée sur la figure 1 avec des tailles de patch variées. Le coefficient de réflexion de l'absorbeur métasurface-graphène avec le potentiel chimique μ _c =0,4 ev est affiché sur la figure 6. Selon la théorie et le modèle de la ligne de transmission, l'impédance Z _mg peut être obtenu. La figure 7 montre les composantes réelles et imaginaires de l'impédance récupérée Z _mg avec différentes tailles de patch. D'après la figure 7a, on peut voir que la partie réelle du film métasurface-graphène diminue au début comme la longueur de patch w passe de 17 m à 19,5 m. Cependant, la tendance inverse se retrouve lorsque la fréquence est supérieure à 0,31 THz. D'autre part, la figure 7b indique que la tendance de la partie imaginaire est la même que la première moitié de la figure 7a. De plus, en comparant les Fig. 4 et 5a, nous avons trouvé qu'il y avait une situation similaire dans les Fig. 3 et 7. Cela prouve aussi directement les conclusions ci-dessus.

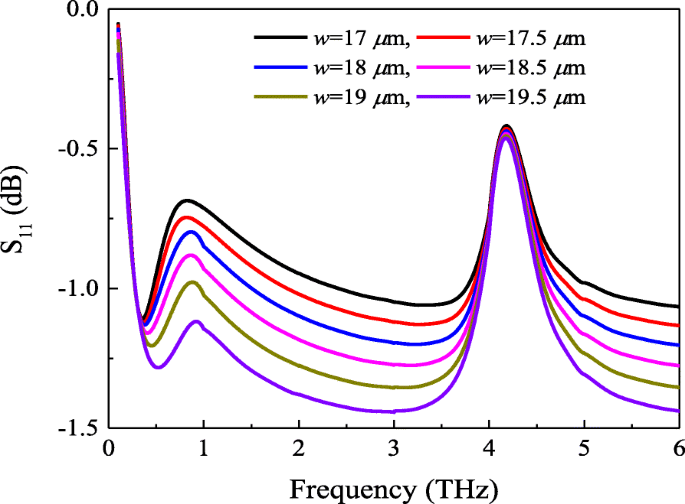
Coefficient de réflexion de l'absorbeur métasurface-graphène avec le potentiel chimique μ _c =0,4 ev

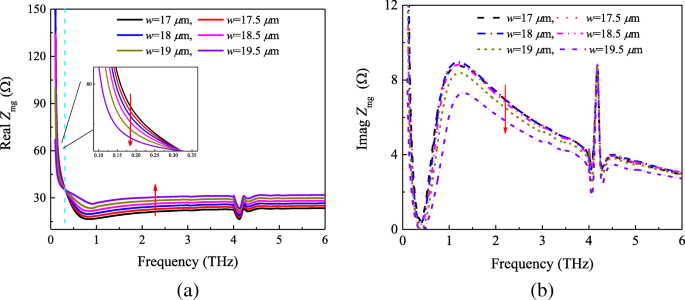
Impédance du film métasurface-graphene Z _mg récupéré de S -paramètres avec le potentiel chimique μ _c =0,4 ev. un Réel et b parties imaginaires

Pour explorer davantage les origines physiques de la résistance de surface en fonction de la taille du patch, les distributions de courant de surface du film de métasurface-graphène en incidence normale sont étudiées à 3 THz. La figure 8 montre la variation de l'intensité du courant pour w =17, 18 et 19 m avec le potentiel chimique μ _c =0,4 ev. La couleur représente l'intensité du champ. De toute évidence, à mesure que la taille augmente, l'amplitude du courant de surface diminue. En tenant compte de l'Éq. 3 et Fig. 7a, lorsque l'intensité du champ électrique est une valeur fixe à 3 THz, l'impédance du film de métasurface-graphène peut être donnée par

$$ {Z}_{mg}\propto w\propto \frac{1}{J}\kern0.5em \left(f>0.32\ \mathrm{THz}\right) $$ (11)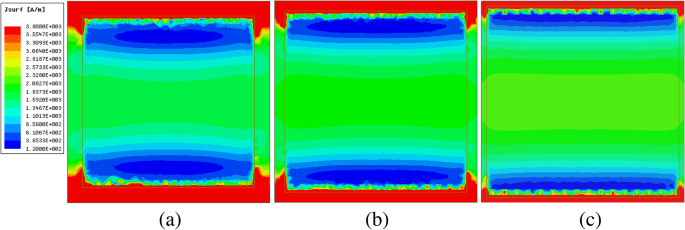

Ampleur du courant de surface avec différentes tailles de patch mais à la même fréquence. un w =17 m, b w =18 m, et c w =19 µm

A partir de la relation (11), nous pouvons trouver que la longueur du patch est inversement proportionnelle à l'amplitude du courant de surface J . L'accord qualitatif entre les résultats simulés et théoriques peut être clairement observé. Pour analyser quantitativement ce phénomène physique, la valeur intégrale de la distribution du courant de surface sur le film de métasurface-graphene est calculée à l'aide du calculateur de champs HFSS, et les valeurs sont 1.10e-6, 1.07e-6 et 1.04e-6 A , respectivement. Ces résultats sont cohérents avec la figure 8.

Conclusions

En résumé, pour un film mince de métasurface-graphène en fréquence THz, les impédances de surface fondamentales et effectives ont été étudiées. Des formules analytiques ont été dérivées et vérifiées pour calculer l'impédance d'un patch carré. Quant à la structure hybride métasurface-graphene, les résultats simulés basés sur le coefficient de réflexion extrait ont été comparés aux résultats analytiques obtenus à partir de la combinaison parallèle des impédances du patch carré et de la feuille de graphène. Une analyse supplémentaire a été réalisée pour discuter de l'effet de la taille du patch sur l'impédance effective. De plus, les relations entre la taille du patch et l'impédance du film ont été expliquées qualitativement et quantification en traçant et en intégrant le courant de surface. Cette méthode d'analyse peut être étendue pour étudier le problème d'impédance avec deux autres couches conductrices différentes. De plus, une simulation numérique approfondie ainsi que l'optimisation analytique des couches composites spécialement appliquées à l'antenne et à l'absorbeur peuvent être évitées par notre analyse effectuée dans ce travail.

Abréviations

HFSS :: Simulation de structure haute fréquence
TEM :: Transversale électromagnétique
THz :: Térahertz

Utilisation de nanoparticules magnétiques chargées positivement pour capturer des bactéries à très faible concentration Livraison d'ARNsi à base de micelles cationiques pour une thérapie génique efficace contre le cancer du côlon

Nanomatériaux