Comment créer un réseau de neurones Perceptron multicouche en Python

Cet article vous guide pas à pas à travers un programme Python qui nous permettra d'entraîner un réseau de neurones et d'effectuer une classification avancée.

Il s'agit de la 12e entrée de la série de développement de réseaux neuronaux d'AAC. Découvrez ce que la série propose d'autre ci-dessous :

1. Comment effectuer une classification à l'aide d'un réseau de neurones :qu'est-ce que le perceptron ?
2. Comment utiliser un exemple simple de réseau neuronal Perceptron pour classer des données
3. Comment former un réseau de neurones Perceptron de base
4. Comprendre la formation simple sur les réseaux neuronaux
5. Une introduction à la théorie de la formation pour les réseaux de neurones
6. Comprendre le taux d'apprentissage dans les réseaux de neurones
7. Apprentissage automatique avancé avec le Perceptron multicouche
8. La fonction d'activation sigmoïde :activation dans les réseaux de neurones Perceptron multicouches
9. Comment former un réseau de neurones Perceptron multicouches
10. Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches
11. Architecture de réseau neuronal pour une implémentation Python
12. Comment créer un réseau de neurones Perceptron multicouche en Python
13. Traitement du signal à l'aide de réseaux de neurones :validation dans la conception de réseaux de neurones
14. Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Dans cet article, nous allons prendre le travail que nous avons fait sur les réseaux de neurones Perceptron et apprendre comment en implémenter un dans un langage familier :Python.

Développement de code Python compréhensible pour les réseaux de neurones

Récemment, j'ai examiné pas mal de ressources en ligne pour les réseaux de neurones, et bien qu'il y ait sans aucun doute beaucoup de bonnes informations, je n'étais pas satisfait des implémentations logicielles que j'ai trouvées. Ils étaient toujours trop complexes, ou trop denses, ou pas assez intuitifs. Quand j'écrivais mon réseau de neurones Python, je voulais vraiment faire quelque chose qui pourrait aider les gens à apprendre comment le système fonctionne et comment la théorie des réseaux de neurones est traduite en instructions de programme.

Cependant, il existe parfois une relation inverse entre la clarté du code et l'efficacité du code. Le programme dont nous allons parler dans cet article n'est certainement pas optimisé pour des performances rapides. L'optimisation est un problème sérieux dans le domaine des réseaux de neurones ; les applications réelles peuvent nécessiter d'immenses quantités de formation, et par conséquent une optimisation approfondie peut conduire à des réductions significatives du temps de traitement. Cependant, pour des expériences simples comme celles que nous allons faire, la formation ne prend pas très longtemps, et il n'y a aucune raison de s'inquiéter des pratiques de codage qui privilégient la simplicité et la compréhension à la vitesse.

L'intégralité du programme Python est incluse sous forme d'image à la fin de cet article et le fichier ("MLP_v1.py") est fourni en téléchargement. Le code effectue à la fois l'apprentissage et la validation ; cet article se concentre sur la formation, et nous discuterons de la validation plus tard. Dans tous les cas, cependant, il n'y a pas beaucoup de fonctionnalités dans la partie validation qui ne sont pas couvertes dans la partie formation.

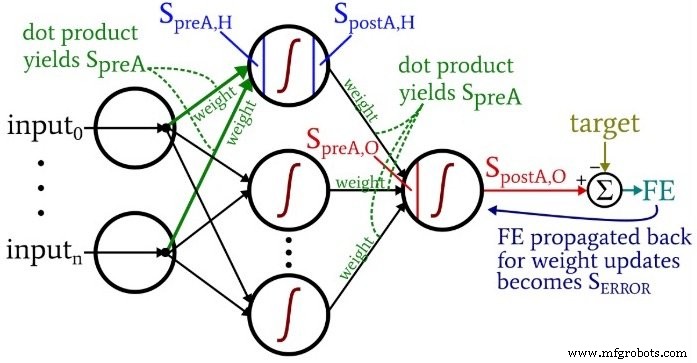
Pendant que vous réfléchissez au code, vous voudrez peut-être revenir sur le diagramme architecture-plus-terminologie légèrement écrasant mais très informatif que j'ai fourni dans la partie 10.

Préparation des fonctions et des variables

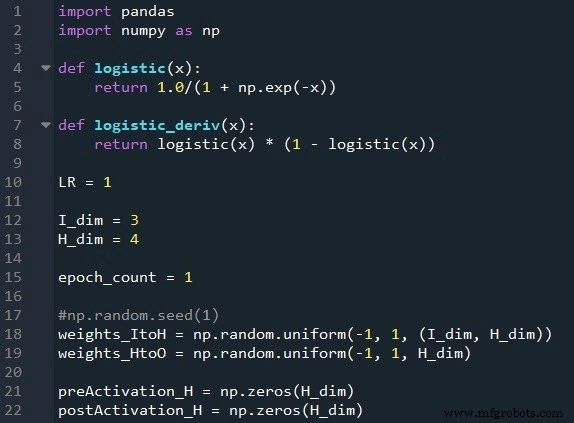
La bibliothèque NumPy est largement utilisée pour les calculs du réseau, et la bibliothèque Pandas me donne un moyen pratique d'importer des données d'entraînement à partir d'un fichier Excel.

Comme vous le savez déjà, nous utilisons la fonction logistique sigmoïde pour l'activation. Nous avons besoin de la fonction logistique elle-même pour calculer les valeurs de postactivation, et la dérivée de la fonction logistique est requise pour la rétropropagation.

Ensuite, nous choisissons le taux d'apprentissage, la dimensionnalité de la couche d'entrée, la dimensionnalité de la couche cachée et le nombre d'époques. L'entraînement sur plusieurs époques est important pour les vrais réseaux de neurones, car il vous permet d'extraire plus d'apprentissage de vos données d'entraînement. Lorsque vous générez des données d'entraînement dans Excel, vous n'avez pas besoin d'exécuter plusieurs époques, car vous pouvez facilement créer plus d'échantillons d'entraînement.

Le np.random.uniform() La fonction remplit nos deux matrices de poids avec des valeurs aléatoires comprises entre –1 et +1. (Notez que la matrice cachée-à-sortie n'est en fait qu'un tableau, car nous n'avons qu'un seul nœud de sortie.) Le np.random.seed(1) L'instruction fait que les valeurs aléatoires sont les mêmes à chaque fois que vous exécutez le programme. Les valeurs de poids initiales peuvent avoir un effet significatif sur les performances finales du réseau formé, donc si vous essayez d'évaluer comment autre variables améliorent ou dégradent les performances, vous pouvez décommenter cette instruction et ainsi éliminer l'influence de l'initialisation de poids aléatoire.

Enfin, je crée des tableaux vides pour les valeurs de préactivation et de postactivation dans la couche cachée.

Importation des données d'entraînement

C'est la même procédure que celle que j'ai utilisée dans la partie 4. J'importe les données d'entraînement d'Excel, sépare les valeurs cibles dans la colonne « sortie », supprime la colonne « sortie », convertit les données d'entraînement en une matrice NumPy et stocke le nombre d'échantillons d'entraînement dans le training_count variable.

Traitement anticipé

Les calculs qui produisent une valeur de sortie et dans lesquels les données se déplacent de gauche à droite dans un diagramme de réseau neuronal typique, constituent la partie « anticipation » du fonctionnement du système. Voici le code du feedforward :

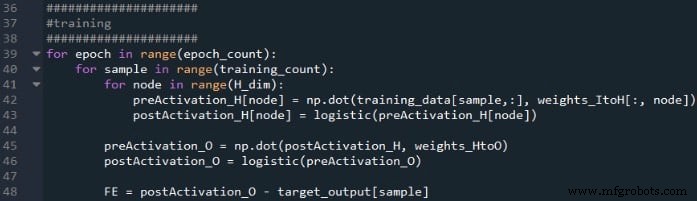
La première boucle for nous permet d'avoir plusieurs époques. Au sein de chaque époque, nous calculons une valeur de sortie (c'est-à-dire le signal de postactivation du nœud de sortie) pour chaque échantillon, et cette opération échantillon par échantillon est capturée par la seconde boucle for. Dans la troisième boucle for, nous nous occupons individuellement de chaque nœud caché, en utilisant le produit scalaire pour générer le signal de préactivation et la fonction d'activation pour générer le signal de postactivation.

Après cela, nous sommes prêts à calculer le signal de préactivation pour le nœud de sortie (en utilisant à nouveau le produit scalaire), et nous appliquons la fonction d'activation pour générer le signal de postactivation. Ensuite, nous soustrayons la cible du signal de postactivation du nœud de sortie pour calculer l'erreur finale.

Rétropropagation

Après avoir effectué les calculs d'anticipation, il est temps d'inverser les directions. Dans la partie rétropropagation du programme, nous passons du nœud de sortie vers les poids cachés-à-sortie, puis les poids entrée-à-caché, apportant avec nous les informations d'erreur que nous utilisons pour former efficacement le réseau.

Nous avons ici deux couches de boucles for :une pour les poids cachés-à-sortie et une pour les poids entrée-à-caché. Nous générons d'abord S_ERROR , dont nous avons besoin pour calculer à la fois le gradient_HtoO et dégradé_ItoH , puis nous mettons à jour les poids en soustrayant le gradient multiplié par le taux d'apprentissage.

Remarquez comment les poids d'entrée à caché sont mis à jour dans la boucle cachée-sortie. Nous commençons par le signal d'erreur qui ramène à l'un des nœuds cachés, puis nous étendons ce signal d'erreur à tous les nœuds d'entrée qui sont connectés à ce nœud caché :

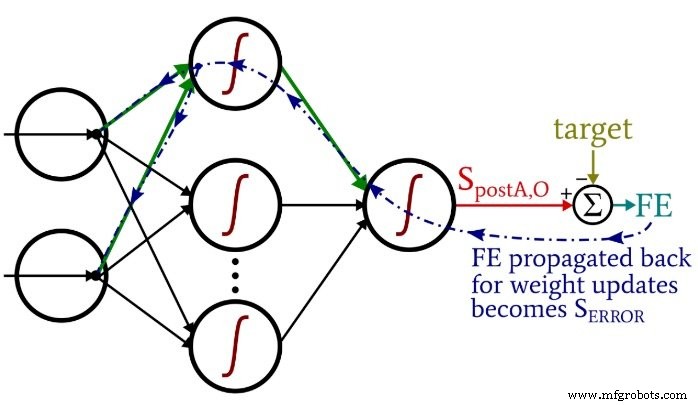
Une fois que tous les poids (ItoH et HtoO) associés à ce nœud caché ont été mis à jour, nous revenons en arrière et recommençons avec le nœud caché suivant.

A noter également que les poids ItoH sont modifiés avant les poids HtoO. Nous utilisons le poids HtoO actuel lorsque nous calculons le gradient_ItoH , nous ne voulons donc pas modifier les poids HtoO avant que ce calcul n'ait été effectué.

Conclusion

Il est intéressant de penser à la quantité de théorie qui a été investie dans ce programme Python relativement court. J'espère que ce code vous aidera à vraiment comprendre comment nous pouvons implémenter un réseau de neurones Perceptron multicouche dans un logiciel.

Vous pouvez trouver mon code complet ci-dessous :

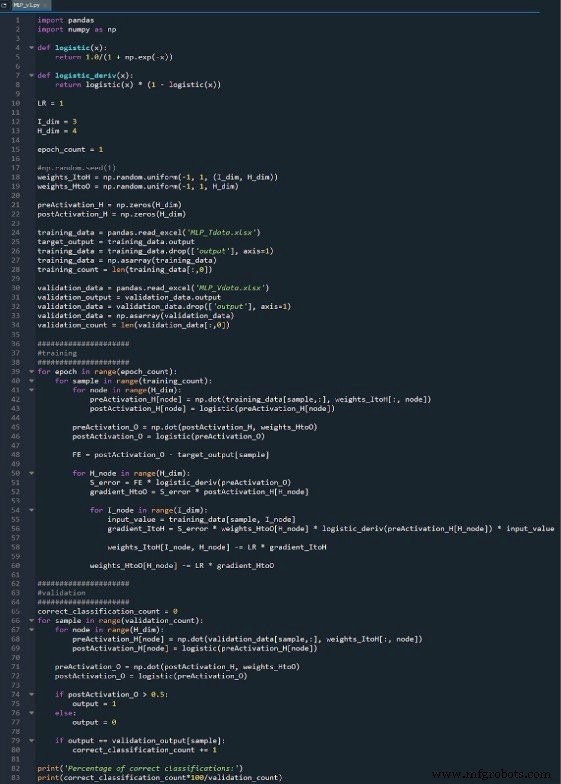
Code de téléchargement