Fonctions de logique numérique

Nous pouvons construire des fonctions logiques simples pour notre circuit de lampe hypothétique, en utilisant plusieurs contacts, et documenter ces circuits assez facilement et de manière compréhensible avec des échelons supplémentaires à notre "échelle" d'origine.

Si nous utilisons une notation binaire standard pour l'état des interrupteurs et de la lampe (0 pour non actionné ou hors tension; 1 pour actionné ou sous tension), une table de vérité peut être faite pour montrer comment fonctionne la logique :

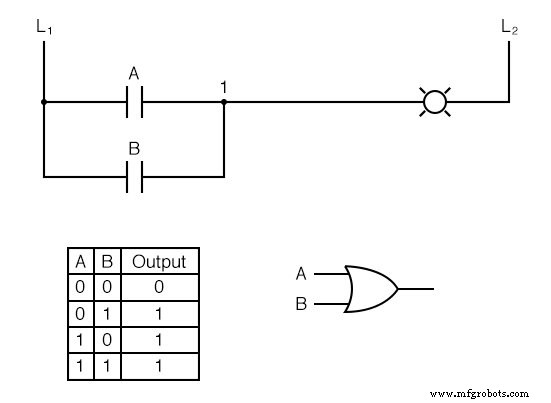
Maintenant, la lampe s'allumera si le contact A ou le contact B est actionné, car tout ce qu'il faut pour que la lampe soit alimentée est d'avoir au moins un chemin pour le courant du fil L₁ au câble 1.

Ce que nous avons est une simple fonction logique OU, implémentée avec rien de plus que des contacts et une lampe.

On peut mimer la fonction logique ET en câblant les deux contacts en série plutôt qu'en parallèle :

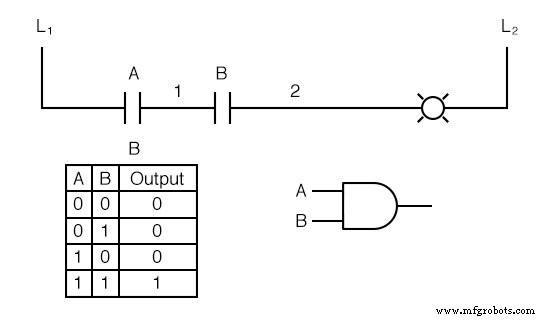
Maintenant, la lampe ne s'allume que si contact A et contact B sont actionnés simultanément.

Un chemin existe pour le courant du fil L₁ à la lampe (fil 2) si et seulement si les deux les contacts de l'interrupteur sont fermés.

La fonction d'inversion logique, ou NON, peut être exécutée sur une entrée de contact simplement en utilisant un contact normalement fermé au lieu d'un contact normalement ouvert :

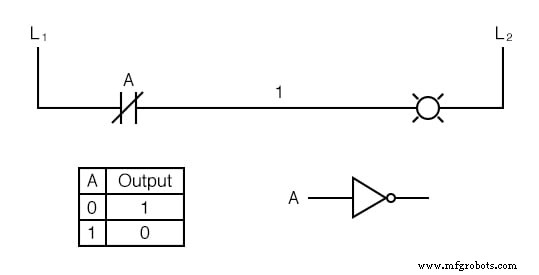
Maintenant, la lampe s'allume si le contact n'est pas actionné et se désexcite lorsque le contact est actionné.

Si nous prenons notre fonction OU et inversons chaque "entrée" en utilisant des contacts normalement fermés, nous nous retrouverons avec une fonction NAND.

Dans une branche spéciale des mathématiques connue sous le nom d'algèbre booléenne , cet effet du changement d'identité de la fonction de porte avec l'inversion des signaux d'entrée est décrit par le théorème de DeMorgan , un sujet qui sera exploré plus en détail dans un chapitre ultérieur.

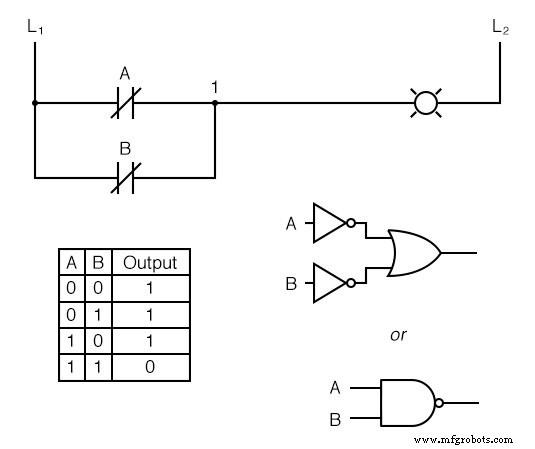
La lampe sera alimentée si soit le contact n'est pas actionné. Il ne s'éteindra que si les deux les contacts sont actionnés simultanément.

De même, si nous prenons notre fonction AND et inversons chaque "entrée" en utilisant des contacts normalement fermés, nous nous retrouverons avec une fonction NOR :

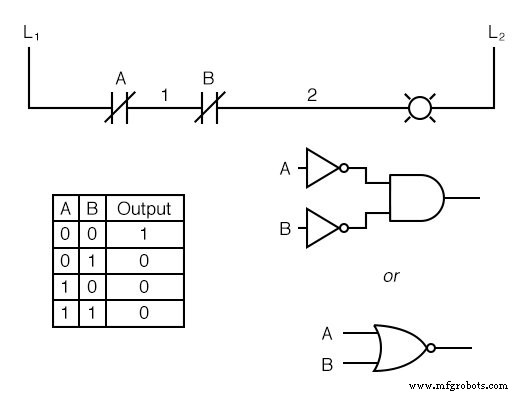
Un modèle se révèle rapidement lorsque les circuits en échelle sont comparés à leurs homologues à portes logiques :

• Les contacts parallèles sont équivalents à une porte OU.
• Les contacts en série sont équivalents à une porte ET.
• Les contacts normalement fermés sont équivalents à une porte NON (onduleur).

Nous pouvons également créer des fonctions logiques combinatoires en regroupant les contacts dans des arrangements série-parallèle. Dans l'exemple suivant, nous avons une fonction OU-exclusif construite à partir d'une combinaison de portes ET, OU et inverseur (NON) :

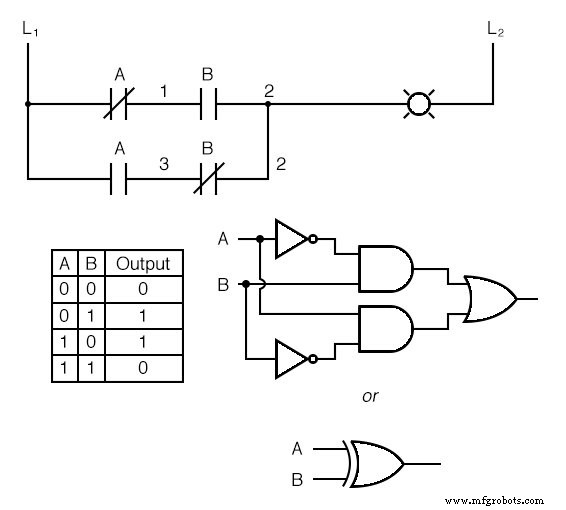
L'échelon supérieur (contact NF A en série avec contact NO B) est l'équivalent de la combinaison de porte NON/ET supérieure.

L'échelon inférieur (contact NO A en série avec contact NF B) est l'équivalent de la combinaison de porte NON/ET inférieure.

La connexion parallèle entre les deux échelons du fil numéro 2 forme l'équivalent de la porte OU, en permettant à l'échelon 1 ou à l'échelon 2 d'alimenter la lampe.

Concevoir une fonction OU-exclusif

Pour réaliser la fonction OU-Exclusif, nous avons dû utiliser deux contacts par entrée :un pour l'entrée directe et l'autre pour l'entrée « inversée ».

Les deux contacts "A" sont physiquement actionnés par le même mécanisme, de même que les deux contacts "B".

L'association commune entre les contacts est indiquée par l'étiquette du contact.

Il n'y a pas de limite au nombre de contacts par commutateur pouvant être représentés dans un schéma à contacts, car chaque nouveau contact sur n'importe quel commutateur ou relais (normalement ouvert ou normalement fermé) utilisé dans le schéma est simplement marqué de la même étiquette.

Parfois, plusieurs contacts sur un seul interrupteur (ou relais) sont désignés par des étiquettes composées, telles que "A-1" et "A-2" au lieu de deux étiquettes "A".

Cela peut être particulièrement utile si vous souhaitez désigner spécifiquement quel ensemble de contacts sur chaque commutateur ou relais est utilisé pour quelle partie d'un circuit.

Par souci de simplicité, je m'abstiendrai d'un étiquetage aussi élaboré dans cette leçon. Si vous voyez une étiquette commune pour plusieurs contacts, vous savez que ces contacts sont tous actionnés par le même mécanisme.

Si l'on souhaite inverser la sortie de toute fonction logique générée par un commutateur, nous devons utiliser un relais avec un contact normalement fermé.

Par exemple, si nous voulons alimenter une charge basée sur l'inverse, ou NON, d'un contact normalement ouvert, nous pourrions faire ceci :

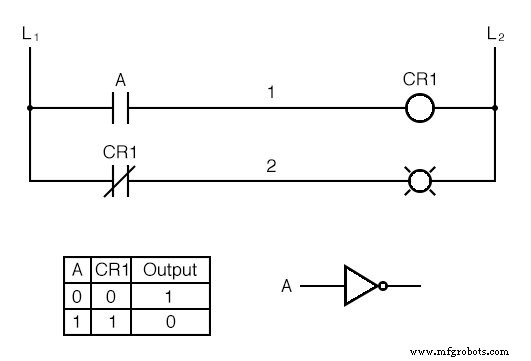
Nous appellerons le relais « relais de contrôle 1 » ou CR₁ . Lorsque la bobine de CR₁ (symbolisé par la paire de parenthèses sur le premier échelon) est alimenté, le contact sur le deuxième échelon s'ouvre , mettant ainsi la lampe hors tension.

Du commutateur A à la bobine de CR₁ , la fonction logique est non inversée. Le contact normalement fermé actionné par la bobine de relais CR₁ fournit une fonction d'inverseur logique pour entraîner la lampe à l'opposé de l'état d'actionnement de l'interrupteur.

En appliquant cette stratégie d'inversion à l'une de nos fonctions d'entrée inversée créées précédemment, telles que OR-to-NAND, nous pouvons inverser la sortie avec un relais pour créer une fonction non inversée :

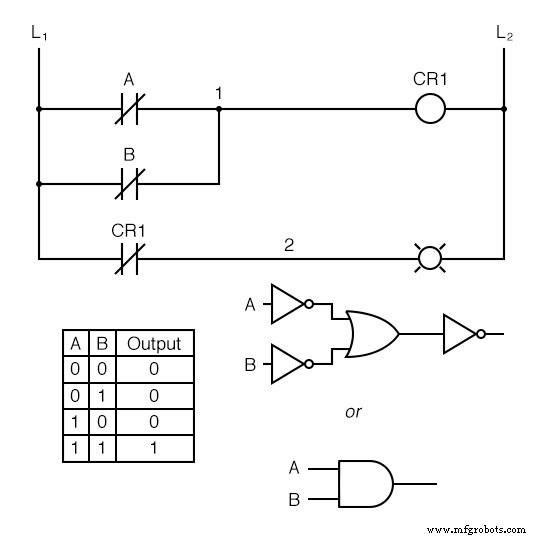
Des interrupteurs à la bobine de CR₁ , la fonction logique est celle d'une porte NAND. CR₁ Le contact normalement fermé de " fournit une inversion finale pour transformer la fonction NAND en fonction ET.

RÉVISER :

• Les contacts parallèles sont logiquement équivalents à une porte OU.
• Les contacts en série sont logiquement équivalents à une porte ET.
• Les contacts normalement fermés (N.C.) sont logiquement équivalents à une porte NON.
• Un relais doit être utilisé pour inverser la sortie d'une fonction de porte logique, tandis que de simples contacts de commutation normalement fermés sont suffisants pour représenter des entrées de porte inversée .

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail d'algèbre booléenne
• Fiche de travail sur la logique des relais électromécaniques
• Fiche de travail sur les signaux logiques numériques