Circuits de calcul

Lorsque quelqu'un mentionne le mot « ordinateur », un appareil numérique est ce qui lui vient généralement à l'esprit. Les circuits numériques représentent des quantités numériques en binaire format :motifs de 1 et de 0 représentés par une multitude de circuits à transistors fonctionnant dans des états saturés ou coupés. Cependant, les circuits analogiques peuvent également être utilisés pour représenter des quantités numériques et effectuer des calculs mathématiques, en utilisant des signaux de tension variables au lieu d'états marche/arrêt discrets.

Voici un exemple simple de représentation binaire (numérique) par rapport à la représentation analogique du nombre « vingt-cinq : »

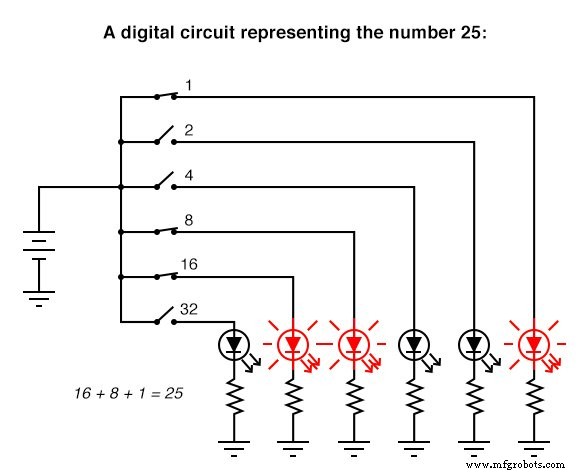
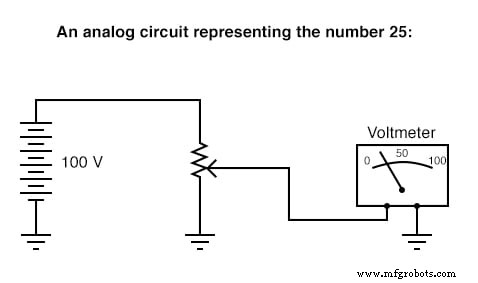
Les circuits numériques sont très différents des circuits construits sur des principes analogiques. Les circuits de calcul numériques peuvent être incroyablement complexes et les calculs doivent souvent être effectués par « étapes » séquentielles pour obtenir une réponse finale, un peu comme un être humain effectuerait des calculs arithmétiques par étapes avec un crayon et du papier. Les circuits de calcul analogiques, en revanche, sont assez simples en comparaison et effectuent leurs calculs de manière continue et en temps réel. Il y a cependant un inconvénient à utiliser des circuits analogiques pour représenter des nombres :l'imprécision. Le circuit numérique illustré ci-dessus représente le nombre vingt-cinq, précisément. Le circuit analogique illustré ci-dessus peut ou non être exactement calibré à 25 000 volts, mais est sujet à une « dérive » et à des erreurs.

Dans les applications où la précision n'est pas critique, les circuits de calcul analogiques sont très pratiques et élégants. Voici quelques circuits d'amplificateurs opérationnels pour effectuer des calculs analogiques :

Circuits d'amplificateurs opérationnels de calcul

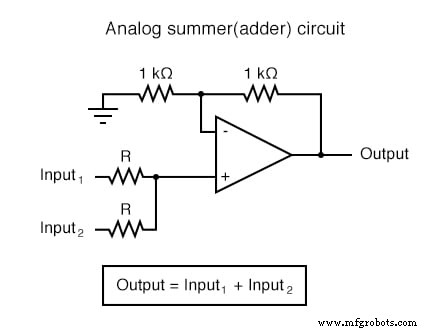
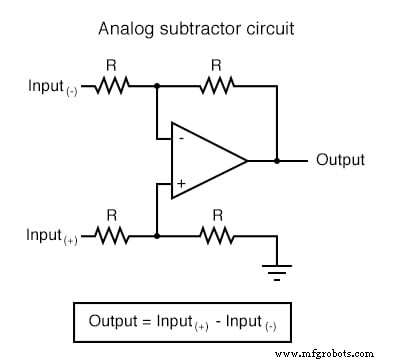
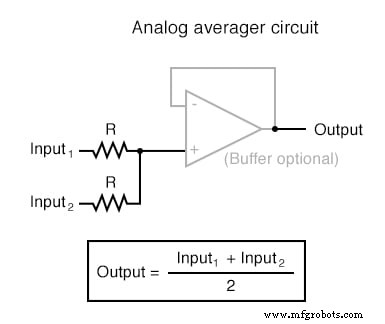
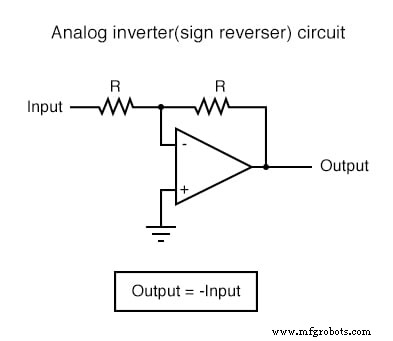
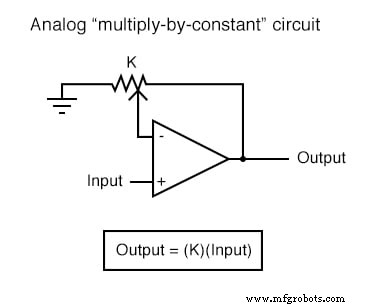
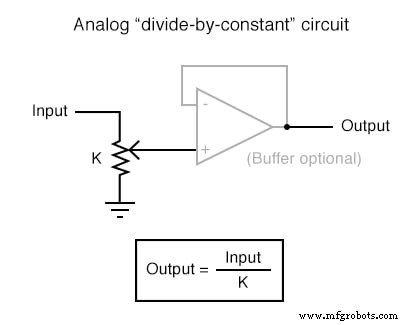
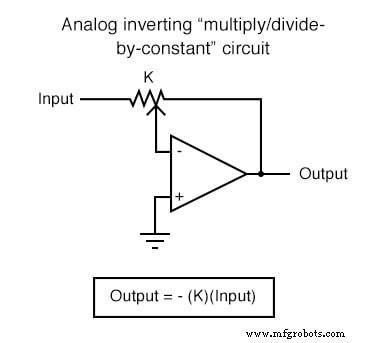
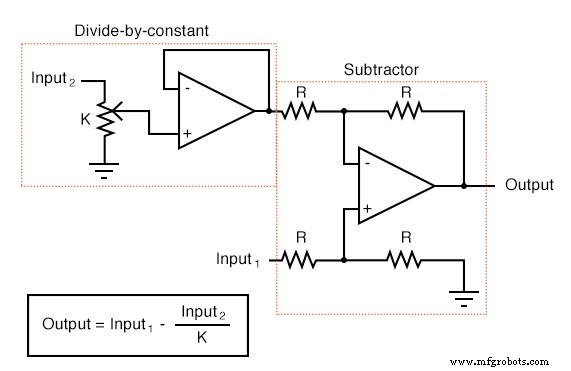
Chacun de ces circuits peut être utilisé de façon modulaire pour créer un circuit capable de multiples calculs. Par exemple, supposons que nous devions soustraire une certaine fraction d'une variable d'une autre variable. En combinant un circuit diviseur par constante avec un circuit soustracteur, nous pourrions obtenir la fonction recherchée :

Appareils appelés ordinateurs analogiques était autrefois courant dans les universités et les ateliers d'ingénierie, où des dizaines de circuits d'amplificateurs opérationnels pouvaient être « rectifiés » avec des cavaliers amovibles pour modéliser des déclarations mathématiques, généralement dans le but de simuler un processus physique dont les équations sous-jacentes étaient connues. Les ordinateurs numériques ont rendu les ordinateurs analogiques presque obsolètes, mais les circuits de calcul analogiques ne peuvent pas être battus par le numérique en termes d'élégance pure et d'économie des composants nécessaires.

Les circuits de calcul analogiques excellent dans l'exécution des opérations de calcul d'intégration et différenciation par rapport au temps, en utilisant des condensateurs dans une boucle de rétroaction d'amplificateur opérationnel. Cependant, pour bien comprendre le fonctionnement et les applications de ces circuits, nous devons d'abord saisir la signification de ces concepts fondamentaux du calcul. Heureusement, l'application de circuits d'amplificateurs opérationnels à des problèmes réels impliquant le calcul constitue un excellent moyen d'enseigner le calcul de base. Selon les mots de John I. Smith, tirés de son livre exceptionnel, Modern Operational Circuit Design :

« Une note d'encouragement est offerte à certains lecteurs :le calcul intégral est l'une des disciplines mathématiques que les circuits [amplificateurs] opérationnels exploitent et, ce faisant, démolit plutôt comme barrière à la compréhension. » (p. 4)

Les sentiments de M. Smith sur la valeur pédagogique des circuits analogiques en tant qu'outil d'apprentissage des mathématiques ne sont pas uniques. Considérez l'opinion de l'ingénieur George Fox Lang, dans un article qu'il a écrit pour le numéro d'août 2000 de la revue Sound and Vibration , intitulé :« Analog n'était pas une marque informatique !" :

« Créer une entité physique réelle (un circuit) régie par un ensemble particulier d'équations et interagir avec elle fournit un aperçu unique de ces déclarations mathématiques. Il n'y a pas de meilleur moyen de développer une « intuition » pour l'interaction entre la physique et les mathématiques que de faire l'expérience d'une telle interaction. L'ordinateur analogique était un puissant outil d'enseignement interdisciplinaire; son obsolescence est pleurée par de nombreux éducateurs dans une variété de domaines. » (p. 23)

La différenciation est la première opération généralement apprise par les étudiants débutants en calcul. En termes simples, la différenciation détermine le taux de changement instantané d'une variable par rapport à une autre. Dans les circuits différenciateurs analogiques, la variable indépendante est le temps, et donc les taux de changement auxquels nous avons affaire sont les taux de changement pour un signal électronique (tension ou courant) par rapport au temps.

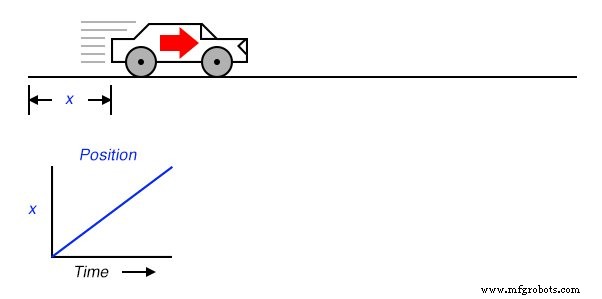
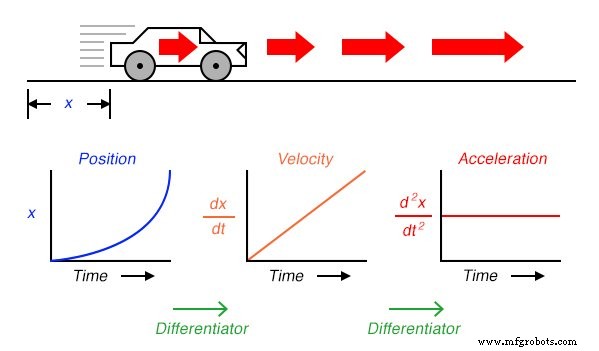
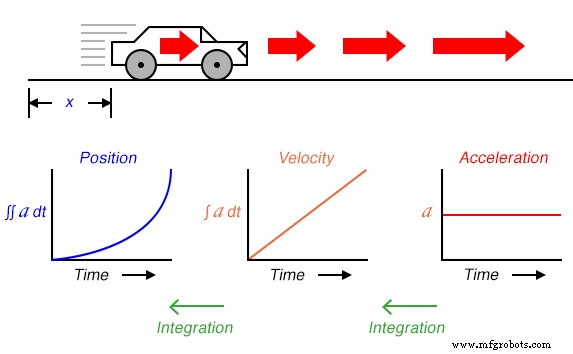
Supposons que nous devions mesurer la position d'une voiture, se déplaçant dans un chemin direct (pas de virages), à partir de son point de départ. Appelons cette mesure, x . Si la voiture se déplace à une vitesse telle que sa distance par rapport au « départ » augmente régulièrement au fil du temps, sa position sera tracée sur un graphique sous la forme d'une linéaire fonction (ligne droite) :

Si nous devions calculer la dérivé de la position de la voiture par rapport au temps (c'est-à-dire déterminer le taux de variation de la position de la voiture par rapport au temps), nous arriverions à une quantité représentant la vitesse de la voiture. La fonction de différenciation est représentée par la notation fractionnaire d/d , donc lors de la différenciation de position (x ) par rapport au temps (t ), on note le résultat (la dérivée) par dx/dt :

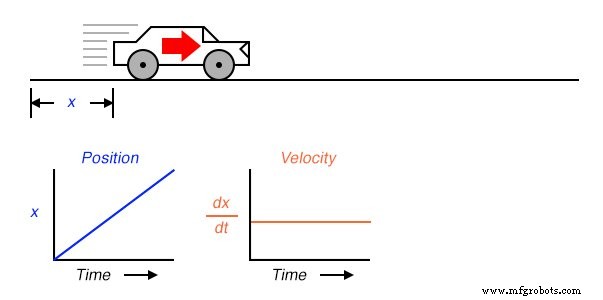
Pour un graphique linéaire de x au fil du temps, la dérivée de la position (dx/dt ), autrement et plus communément appelée vitesse , sera une ligne plate, dont la valeur ne changera pas. La dérivée d'une fonction mathématique peut être comprise graphiquement comme sa pente lorsqu'il est tracé sur un graphique, et ici nous pouvons voir que la position (x ) le graphique a une pente constante, ce qui signifie que sa dérivée (dx/dt ) doit être constant dans le temps.

Maintenant, supposons que la distance parcourue par la voiture augmente de façon exponentielle au fil du temps :c'est-à-dire qu'elle a commencé son voyage par des mouvements lents, mais a parcouru une distance supplémentaire à chaque période de temps. On verrait alors que la dérivée de position (dx/dt ), autrement connu sous le nom de vitesse (v ), ne serait pas constant dans le temps, mais augmenterait :

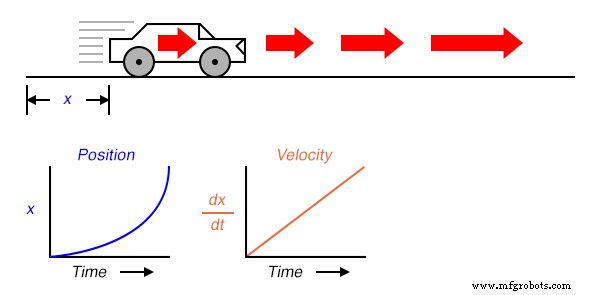
La hauteur des points sur le graphique de vitesse correspond aux taux de variation, ou pente, des points aux moments correspondants sur le graphique de position :

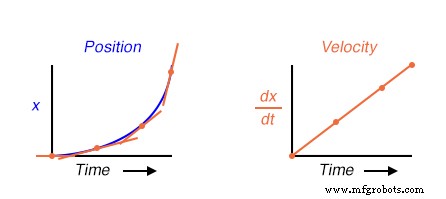
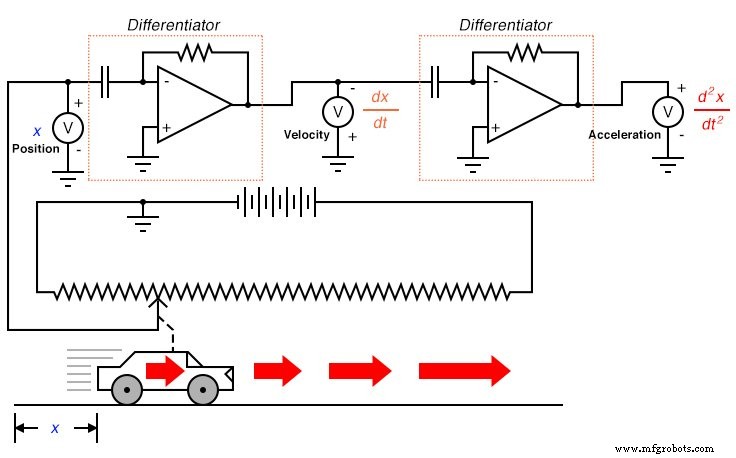
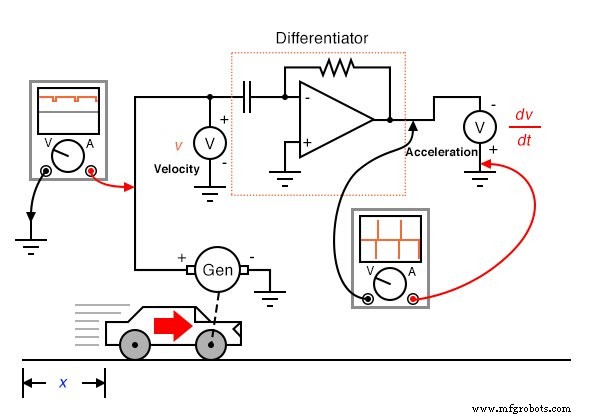
Qu'est-ce que cela a à voir avec les circuits électroniques analogiques? Eh bien, si nous devions avoir un signal de tension analogique représentant la position de la voiture (pensez à un énorme potentiomètre dont l'essuie-glace était attaché à la voiture, générant une tension proportionnelle à la position de la voiture), nous pourrions connecter un circuit différenciateur à ce signal et avoir le circuit calculer en continu la vitesse de la voiture, affichant le résultat via un voltmètre connecté à la sortie du circuit différenciateur :

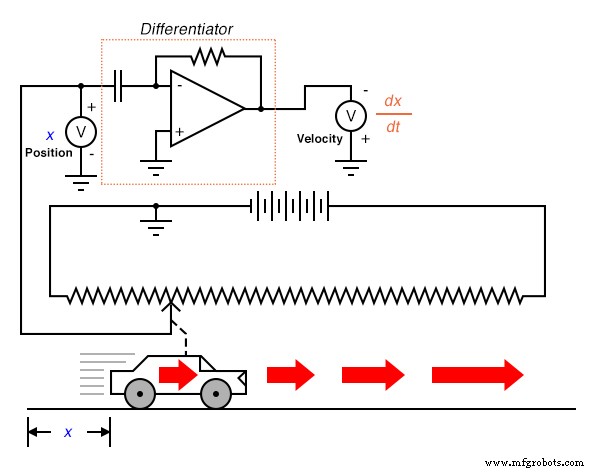
Rappelez-vous du dernier chapitre qu'un circuit différenciateur produit une tension proportionnelle au taux de variation de la tension d'entrée dans le temps (d/dt ). Ainsi, si la tension d'entrée change au fil du temps à un taux constant , la tension de sortie sera à une valeur constante. Si la voiture se déplace de telle manière que sa distance écoulée au fil du temps s'accumule à un rythme constant, cela signifie que la voiture se déplace à une vitesse constante, et le circuit différenciateur produira une tension constante proportionnelle à cette vitesse. Si la distance parcourue par la voiture au fil du temps change de manière non constante, la sortie du circuit différenciateur sera également non constante, mais toujours à un niveau représentatif du taux de variation de l'entrée au fil du temps.

Notez que le voltmètre enregistrant la vitesse (à la sortie du circuit différenciateur) est connecté en polarité « inverse » à la sortie de l'ampli-op. En effet, le circuit différenciateur illustré est inversant :sortie d'une tension négative pour un taux de variation de tension d'entrée positif. Si nous souhaitons que le voltmètre enregistre une valeur positive pour la vitesse, il devra être connecté à l'ampli-op comme indiqué. Aussi peu pratique que cela puisse être de connecter un potentiomètre géant à un objet en mouvement tel qu'une automobile, le concept doit être clair :en effectuant électroniquement la fonction de calcul de différenciation sur un signal représentant la position, nous obtenons un signal représentant la vitesse.

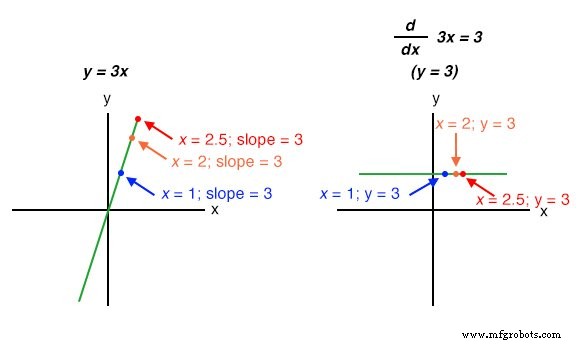
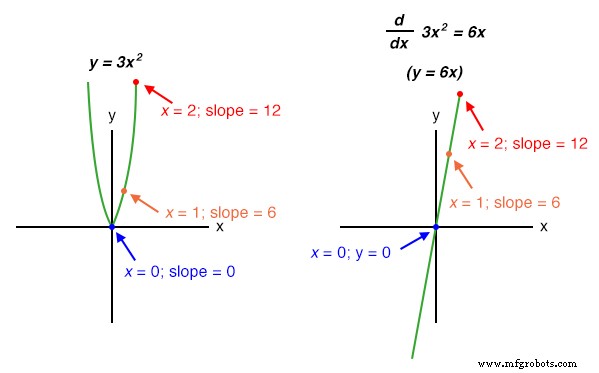
Les étudiants débutants en calcul apprennent les techniques symboliques de différenciation. Cependant, cela nécessite que l'équation décrivant le graphe d'origine soit connue. Par exemple, les étudiants en calcul apprennent à prendre une fonction telle que y =3x et trouver sa dérivée par rapport à x (d/dx ), 3 , simplement en manipulant l'équation. Nous pouvons vérifier l'exactitude de cette manipulation en comparant les graphiques des deux fonctions :

Fonctions non linéaires telles que y =3x ² peut également être différenciée par des moyens symboliques. Dans ce cas, la dérivée de y =3x ² par rapport à x est 6x :

Dans la vraie vie, cependant, nous ne pouvons souvent pas décrire le comportement d'un événement physique par une simple équation comme y =3x , et donc la différenciation symbolique du type appris par les étudiants en calcul peut être impossible à appliquer à une mesure physique. Si quelqu'un souhaitait déterminer la dérivée de la position de notre voiture hypothétique (dx/dt =vitesse) par des moyens symboliques, ils devraient d'abord obtenir une équation décrivant la position de la voiture dans le temps, basée sur des mesures de position prises à partir d'une expérience réelle - une tâche presque impossible à moins que la voiture ne soit utilisée dans des conditions soigneusement contrôlées conduisant à un très simple graphique de position. Cependant, un circuit différentiateur analogique, en exploitant le comportement d'un condensateur par rapport à la tension, au courant et au temps i =C(dv/dt) , différencie naturellement tout signal réel par rapport au temps, et serait capable de sortir un signal correspondant à la vitesse instantanée (dx/dt ) à n'importe quel moment. En enregistrant le signal de position de la voiture avec le signal de sortie du différenciateur à l'aide d'un enregistreur graphique ou d'un autre appareil d'acquisition de données, les deux graphiques se présenteraient naturellement pour l'inspection et l'analyse.

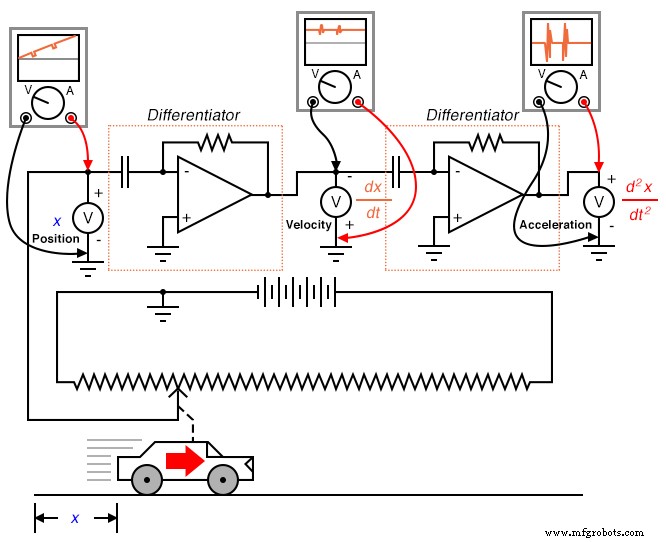
Nous pouvons pousser le principe de différentiation un peu plus loin en l'appliquant au signal de vitesse à l'aide d'un autre circuit différentiateur. En d'autres termes, utilisez-le pour calculer le taux de changement de vitesse, que nous savons être le taux de changement de position. À quelle mesure pratique arriverions-nous si nous faisions cela? Pensez à cela en termes d'unités que nous utilisons pour mesurer la position et la vitesse. Si nous devions mesurer la position de la voiture à partir de son point de départ en miles, nous exprimerions probablement sa vitesse en unités de miles par heure (dx/dt ). Si nous devions différencier la vitesse (mesurée en miles par heure) par rapport au temps, nous nous retrouverions avec une unité de miles par heure par heure . Les cours d'introduction à la physique enseignent aux étudiants le comportement des objets qui tombent, en mesurant la position en mètres , vitesse en mètres par seconde , et changement de vitesse au fil du temps en mètres par seconde, par seconde . Cette dernière mesure est appelée accélération :le taux de changement de vitesse dans le temps :

L'expression d ² x/dt ² est appelée la dérivée seconde de poste (x ) par rapport au temps (t ). Si nous devions connecter un deuxième circuit différenciateur à la sortie du premier, le dernier voltmètre enregistrerait l'accélération :

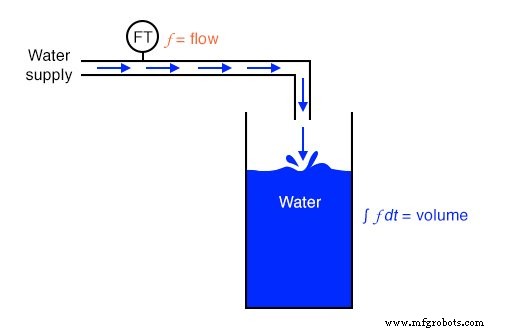
Dérivant la vitesse de la position et l'accélération de la vitesse, nous voyons le principe de différenciation très clairement illustré. Ce ne sont pas les seules mesures physiques liées les unes aux autres de cette manière, mais elles sont peut-être les plus courantes. Un autre exemple de calcul en action est la relation entre le débit de liquide (q ) et le volume de liquide (v ) accumulés dans un navire au fil du temps :

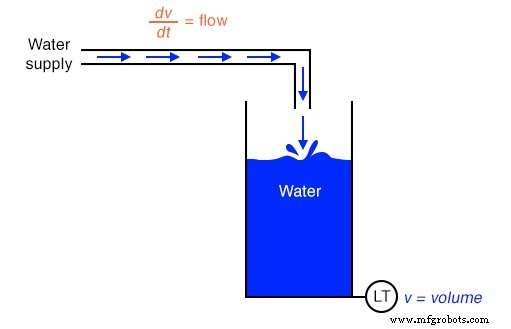
Un dispositif « émetteur de niveau » monté sur un réservoir de stockage d'eau fournit un signal directement proportionnel au niveau d'eau dans le réservoir, qui, si le réservoir a une section transversale constante sur toute sa hauteur, équivaut directement au volume d'eau stocké. Si nous devions prendre ce signal de volume et le différencier par rapport au temps (dv/dt ), on obtiendrait un signal proportionnel au débit d'eau par le tuyau transportant l'eau jusqu'au réservoir. Un circuit différenciateur connecté de manière à recevoir ce signal de volume produirait un signal de sortie proportionnel au débit, se substituant éventuellement à un dispositif de mesure de débit (« Flow Transmitter ») installé dans la canalisation.

Pour en revenir à l'expérience automobile, supposons que notre voiture hypothétique soit équipée d'une génératrice tachymétrique sur l'une des roues, produisant un signal de tension directement proportionnel à la vitesse. Nous pourrions différencier le signal pour obtenir une accélération avec un circuit, comme ceci :

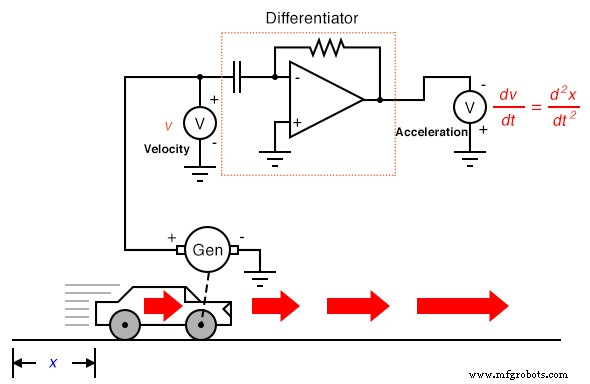
De par sa nature même, la génératrice tachymétrique différencie la position de la voiture dans le temps, générant une tension proportionnelle à la rapidité avec laquelle la position angulaire de la roue change au fil du temps. Cela nous fournit un signal brut déjà représentatif de la vitesse, avec une seule étape de différenciation nécessaire pour obtenir un signal d'accélération. Une génératrice tachymétrique mesurant la vitesse, bien sûr, est un exemple bien plus pratique d'instrumentation automobile qu'un potentiomètre géant mesurant sa position physique, mais ce que nous gagnons en praticité, nous le perdons en mesure de position. Peu importe combien de fois nous différencions, nous ne pouvons jamais déduire la position de la voiture à partir d'un signal de vitesse. Si le processus de différenciation nous a amenés de la position à la vitesse à l'accélération, alors nous devons d'une manière ou d'une autre effectuer le processus de différenciation « inverse » pour passer de la vitesse à la position. Un tel processus mathématique existe, et il s'appelle intégration . Le circuit « intégrateur » peut être utilisé pour réaliser cette fonction d'intégration dans le temps :

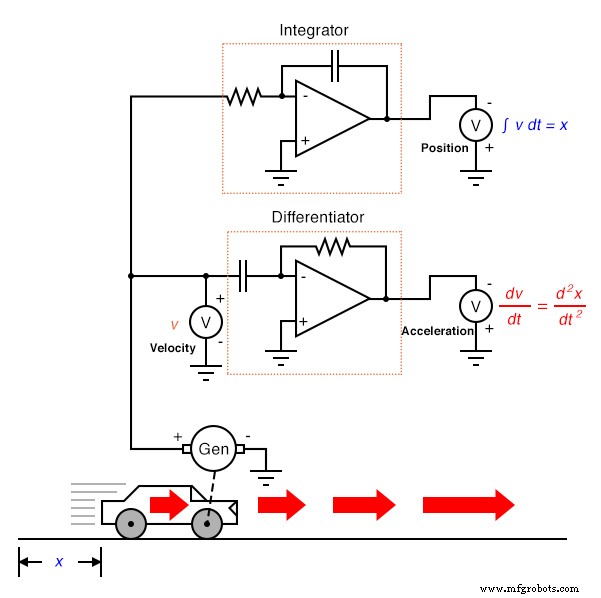
Rappelez-vous du dernier chapitre qu'un circuit intégrateur produit une tension dont le taux de variation dans le temps est proportionnel à l'amplitude de la tension d'entrée. Ainsi, étant donné une tension d'entrée constante, la tension de sortie va changer à un taux constant . Si la voiture se déplace à une vitesse constante (tension constante d'entrée du circuit intégrateur à partir de la génératrice tachymétrique), alors sa distance parcourue augmentera régulièrement au fil du temps et l'intégrateur produira une tension en constante évolution proportionnelle à cette distance. Si la vitesse de la voiture n'est pas constante, le taux de variation dans le temps ne sera pas non plus celui de la sortie du circuit intégrateur, mais la tension de sortie le sera représentent fidèlement la distance parcourue par la voiture à un moment donné.

Le symbole de l'intégration ressemble à une lettre cursive très étroite « S » (∫). L'équation utilisant ce symbole (∫v dt =x ) nous dit que nous intégrons la vitesse (v ) par rapport au temps (dt ), et l'obtention du poste (x ) en conséquence.

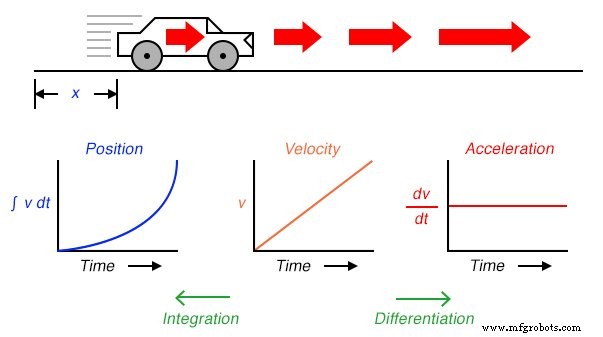
Ainsi, nous pouvons exprimer trois mesures du mouvement de la voiture (position, vitesse et accélération) en termes de vitesse (v ) aussi facilement que l'on pourrait en termes de position (x ):

Si nous avions un accéléromètre attaché à la voiture, générant un signal proportionnel au taux d'accélération ou de décélération, nous pourrions (hypothétiquement) obtenir un signal de vitesse avec une étape d'intégration et un signal de position avec une deuxième étape d'intégration :

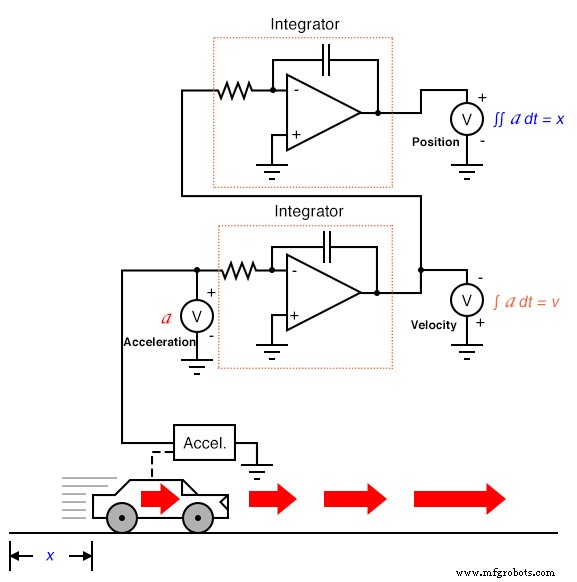
Ainsi, les trois mesures du mouvement de la voiture (position, vitesse et accélération) peuvent être exprimées en termes d'accélération :

Comme vous vous en doutez peut-être, le processus d'intégration peut également être illustré et appliqué à d'autres systèmes physiques. Prenons par exemple le réservoir de stockage d'eau et l'exemple de débit illustré précédemment. Si le débit est le dérivé du volume du réservoir par rapport au temps (q =dv/dt ), alors on pourrait aussi dire que le volume est l'intégrale du débit par rapport au temps :

Si nous devions utiliser un appareil « Flow Transmitter » pour mesurer le débit d'eau, alors par intégration temporelle, nous pourrions calculer le volume d'eau accumulé dans le réservoir au fil du temps. Bien qu'il soit théoriquement possible d'utiliser un circuit intégrateur d'amplificateur opérationnel capacitif pour dériver un signal de volume à partir d'un signal de débit, les dispositifs « intégrateurs » électroniques mécaniques et numériques sont plus adaptés à une intégration sur de longues périodes de temps et sont fréquemment utilisés dans l'eau. industries de traitement et de distribution.

De même qu'il existe des techniques symboliques de différenciation, il existe également des techniques symboliques d'intégration, bien qu'elles tendent à être plus complexes et plus variées. L'application de l'intégration symbolique à un problème du monde réel comme l'accélération d'une voiture, cependant, dépend toujours de la disponibilité d'une équation décrivant avec précision le signal mesuré - une chose souvent difficile ou impossible à dériver des données mesurées. Cependant, les circuits intégrateurs électroniques remplissent cette fonction mathématique en continu, en temps réel, et pour tout profil de signal d'entrée, fournissant ainsi un outil puissant pour les scientifiques et les ingénieurs.

Cela dit, il y a des mises en garde à l'utilisation de techniques de calcul pour dériver un type de mesure d'un autre. La différenciation a la tendance indésirable d'amplifier le « bruit » trouvé dans la variable mesurée, car le bruit apparaîtra généralement sous forme de fréquences beaucoup plus élevées que la variable mesurée, et les hautes fréquences, de par leur nature même, possèdent des taux de changement élevés au fil du temps.

Pour illustrer ce problème, supposons que nous dérivions une mesure de l'accélération de la voiture à partir du signal de vitesse obtenu à partir d'une génératrice tachymétrique avec des balais ou des barres de collecteur usés. Les points de mauvais contact entre le balai et le collecteur produiront des "creux" momentanés de la tension de sortie de la génératrice tachymétrique, et le circuit différenciateur qui y est connecté interprétera ces creux comme des changements très rapides de vitesse. Pour une voiture se déplaçant à vitesse constante - ni en accélération ni en décélération - le signal d'accélération doit être de 0 volt, mais le « bruit » dans le signal de vitesse causé par une génératrice tachymétrique défectueuse entraînera le signal différencié (d'accélération) à contenir des « pointes », indiquant faussement brèves périodes d'accélération et de décélération élevées :

La tension de bruit présente dans un signal à différencier n'a pas besoin d'être d'amplitude significative pour causer des problèmes :il suffit que le profil de bruit ait des temps de montée ou de descente rapides. En d'autres termes, tout bruit électrique avec un dv/dt élevé composante sera problématique lorsqu'elle est différenciée, même si elle est de faible amplitude.

Il convient de noter que ce problème n'est pas un artefact (une erreur idiosyncratique de l'instrument de mesure/calcul) du circuit analogique ; elle est plutôt inhérente au processus de différenciation. Quelle que soit la manière dont nous pouvons effectuer la différenciation, le « bruit » dans le signal de vitesse corrompt invariablement le signal de sortie. Bien sûr, si nous différencions un signal deux fois, comme nous l'avons fait pour obtenir à la fois la vitesse et l'accélération d'un signal de position, le signal de bruit amplifié produit par le premier circuit différentiateur sera à nouveau amplifié par le différentiateur suivant, aggravant ainsi le problème :/P>

L'intégration ne souffre pas de ce problème, car les intégrateurs agissent comme des filtres passe-bas, atténuant les signaux d'entrée à haute fréquence. En effet, tous les pics hauts et bas résultant du bruit sur le signal sont moyennés ensemble au cours du temps, pour un résultat net diminué. On pourrait donc supposer que nous pourrions éviter tous les ennuis en mesurant directement l'accélération et en intégrant ce signal pour obtenir la vitesse; en effet, calculant en « sens inverse » de la manière indiquée précédemment :

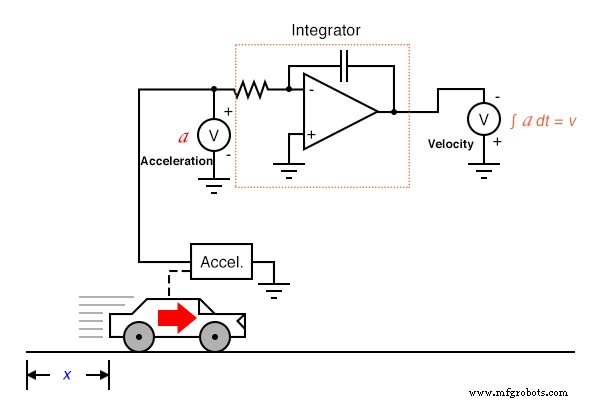
Malheureusement, suivre cette méthodologie pourrait nous conduire à d'autres difficultés, l'une étant un artefact courant des circuits intégrateurs analogiques connu sous le nom de drift . Tous les amplificateurs opérationnels ont une certaine quantité de courant de polarisation d'entrée, et ce courant aura tendance à provoquer une accumulation de charge sur le condensateur en plus de toute charge accumulée en raison du signal de tension d'entrée. En d'autres termes, tous les circuits intégrateurs analogiques souffrent de la tendance à avoir leur tension de sortie « dérive » ou « fluage » même lorsqu'il n'y a absolument aucune entrée de tension, accumulant ainsi des erreurs au fil du temps. De plus, les condensateurs imparfaits auront tendance à perdre leur charge stockée au fil du temps en raison de la résistance interne, ce qui entraînera une « dérive » vers une tension de sortie nulle. Ces problèmes sont artefacts des circuits analogiques, et peuvent être éliminés grâce à l'utilisation de calculs numériques.

Nonobstant les artefacts de circuit, des erreurs possibles peuvent résulter de l'intégration d'une mesure (telle que l'accélération) pour en obtenir une autre (telle que la vitesse) simplement à cause de la façon dont l'intégration fonctionne. Si le point d'étalonnage « zéro » du capteur de signal brut n'est pas parfait, il produira un léger signal positif ou négatif même dans des conditions où il ne devrait rien produire. Considérez une voiture avec un accéléromètre imparfaitement calibré, ou une qui est influencée par la gravité pour détecter une légère accélération sans rapport avec le mouvement de la voiture. Même avec un ordinateur d'intégration parfait, cette erreur de capteur entraînera l'accumulation d'erreurs par l'intégrateur, résultant en un signal de sortie indiquant un changement de vitesse lorsque la voiture n'accélère ni ne décélère.

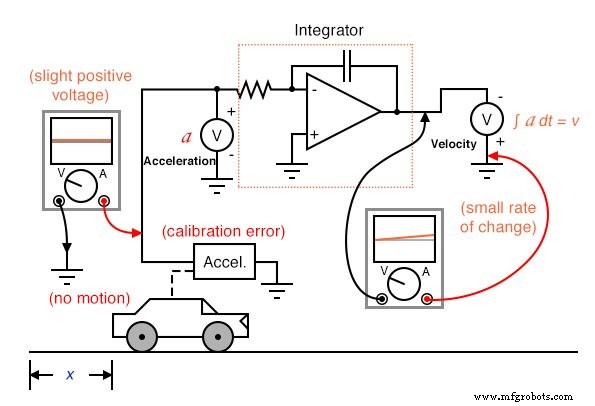
Comme pour la différenciation, cette erreur s'aggravera également si le signal intégré est transmis à un autre circuit intégrateur, car la sortie « dérive » du premier intégrateur présentera très bientôt un signal positif ou négatif important pour le prochain intégrateur à intégrer. Par conséquent, des précautions doivent être prises lors de l'intégration des signaux du capteur :si le réglage « zéro » du capteur n'est pas parfait , le résultat intégré dérivera, même si le circuit intégrateur lui-même est parfait.

Jusqu'à présent, les seules erreurs d'intégration discutées étaient de nature artificielle :elles provenaient d'imperfections dans les circuits et les capteurs. Il existe également une source d'erreur inhérente au processus d'intégration lui-même, et c'est la constante inconnue problème. Les étudiants débutants en calcul apprennent que chaque fois qu'une fonction est intégrée, il existe une constante inconnue (généralement représentée par la variable C ) ajouté au résultat. Cette incertitude est plus facile à comprendre en comparant les dérivées de plusieurs fonctions ne différant que par l'ajout d'une valeur constante :

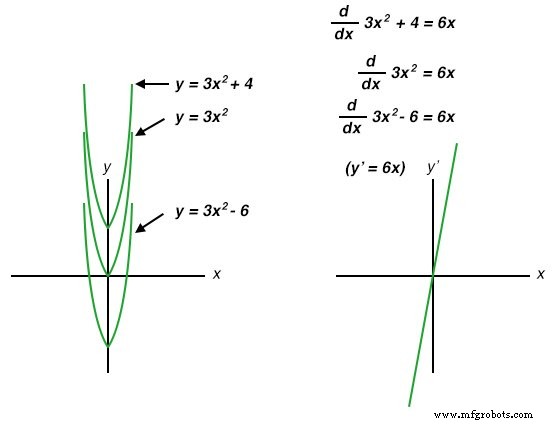
Notez comment chacune des courbes paraboliques (y =3x ² + C ) partagent exactement la même forme, différant les uns des autres en ce qui concerne leur décalage vertical. Cependant, ils partagent tous exactement la même fonction dérivée :y' =(d/dx)( 3x ² + C) =6x , car ils partagent tous des taux de changement identiques (pentes) aux points correspondants le long du x axe. Bien que cela semble assez naturel et attendu du point de vue de la différenciation (différentes équations partageant une dérivée commune), cela semble généralement étrange aux étudiants débutants du point de vue de l'intégration, car il existe plusieurs réponses correctes pour l'intégrale d'une fonction. En passant d'une équation à sa dérivée, il n'y a qu'une seule réponse, mais le retour de cette dérivée à l'équation d'origine nous conduit à une gamme de solutions correctes. En l'honneur de cette incertitude, la fonction symbolique d'intégration est appelée intégrale indéfinie .

Lorsqu'un intégrateur effectue une intégration de signal en direct par rapport au temps, la sortie est la somme du signal d'entrée intégré au cours du temps et une valeur initiale d'amplitude arbitraire, représentant la sortie préexistante de l'intégrateur au moment où l'intégration a commencé. Par exemple, si j'intègre la vitesse d'une voiture roulant en ligne droite à partir d'une ville, en calculant qu'une vitesse constante de 50 miles par heure sur une période de 2 heures produira une distance (∫v dt ) de 100 miles, cela ne signifie pas nécessairement que la voiture sera à 100 miles de la ville après 2 heures. Tout ce qu'il nous dit, c'est que la voiture sera à 100 milles plus loin loin de la ville après 2 heures de route. La distance réelle de la ville après 2 heures de conduite dépend de la distance entre la voiture et la ville lorsque l'intégration a commencé. Si nous ne connaissons pas cette valeur initiale pour la distance, nous ne pouvons pas déterminer la distance exacte de la voiture par rapport à la ville après 2 heures de conduite.

Ce même problème apparaît lorsque l'on intègre l'accélération par rapport au temps pour obtenir la vitesse :

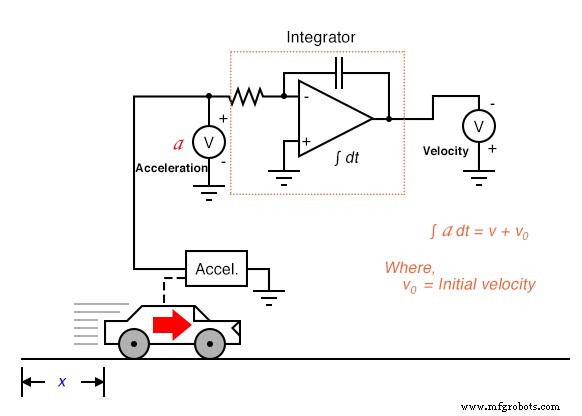
Dans ce système intégrateur, la vitesse calculée de la voiture ne sera valable que si le circuit intégrateur est initialisé à une valeur de sortie de zéro lorsque la voiture est à l'arrêt (v =0). Sinon, l'intégrateur pourrait très bien sortir un signal non nul pour la vitesse (v₀ ) lorsque la voiture est à l'arrêt, car l'accéléromètre ne peut pas faire la différence entre un état stationnaire (0 milles à l'heure) et un état de vitesse constante (disons, 60 milles à l'heure, inchangé). Cette incertitude dans la sortie de l'intégrateur est inhérente au processus d'intégration, et non un artefact du circuit ou du capteur.

En résumé, si une précision maximale est souhaitée pour une mesure physique, il est préférable de mesurer cette variable directement plutôt que de la calculer à partir d'autres mesures. Cela ne veut pas dire que le calcul ne vaut rien. Bien au contraire, c'est souvent le seul moyen pratique d'obtenir une mesure souhaitée. Cependant, les limites du calcul doivent être comprises et respectées afin d'obtenir des mesures précises.

FEUILLE DE TRAVAIL CONNEXE :

• Fiche de travail sur les circuits de calcul linéaires