Deux techniques pour linéariser les ponts de capteurs résistifs

Mesurer les minuscules changements de résistance dans les capteurs résistifs peut être une tâche ardue. Voici deux méthodes matérielles pour éliminer les erreurs de non-linéarité du pont.

La résistance d'un capteur résistif dépend d'une variable physique telle que la température ou la force. Le pourcentage de variation de la résistance de ces dispositifs est généralement faible. Par exemple, la variation totale de la résistance d'une jauge de contrainte peut être inférieure à 1 % sur toute sa plage de fonctionnement.

Discerner ces petites valeurs nécessite des circuits de mesure très précis. Les circuits en pont nous permettent d'effectuer plus facilement ces mesures précises. Cependant, la sortie d'un circuit en pont peut avoir une relation non linéaire avec la variable physique mesurée même si nous utilisons un capteur linéaire.

Dans ces cas, nous pouvons utiliser des techniques logicielles ou matérielles pour éliminer les erreurs de non-linéarité du pont. Dans cet article, nous examinerons deux techniques différentes de linéarisation des ponts de capteurs résistifs.

Non-linéarité du pont des capteurs résistifs

Considérons un capteur de pression résistif avec la réponse linéaire suivante :

\[R_{sensor} =R_0 + Mx\]

où R₀ est la résistance initiale du capteur à pression nulle, x est la valeur du mesurande (pression) et M est la pente de la réponse du capteur. Pour simplifier nos futures équations, supposons que la valeur de M soit égale à la valeur de la résistance initiale du capteur (R₀ ) et par conséquent, la réponse du capteur est \[R_0(1+x)\].

Habituellement, le pourcentage de variation de la résistance d'un capteur résistif est faible et nous devons utiliser un circuit en pont pour effectuer plus facilement des mesures précises. Une configuration de pont courante pour ce capteur est illustrée à la figure 1.

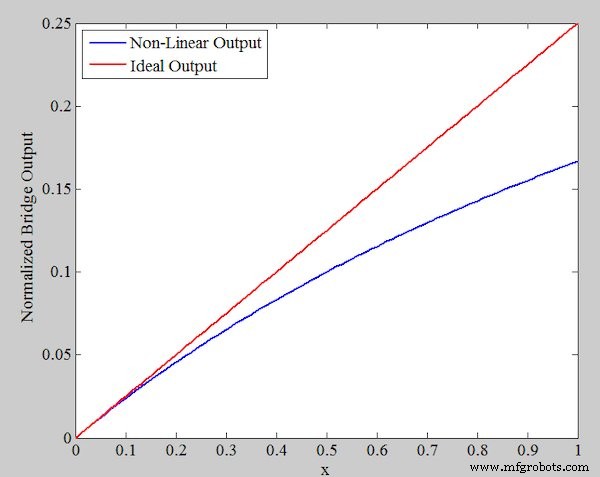
Figure 1. Configuration de pont commun d'un capteur résistif

A noter que les trois autres résistances du pont ont une résistance de R₀ . Ce choix de résistances en pont maximise la sensibilité de la sortie (V_out ) aux modifications de la résistance du capteur. L'équation de sortie peut être obtenue comme :

\[V_{out} =V_A - V_B =V_r\left(\frac{R_0(1+x)}{R_0+R_0(1+x)} - \frac {1}{2}\droit)\]

Cela se simplifie en :

\[V_{out} =V_r\left(\frac{x}{2(2+x)}\right)\]

Équation 1.

Comme vous pouvez le voir, la relation entre la sortie du pont et le changement de la valeur de résistance (x) n'est pas linéaire. Avec \[x\ll2\], nous pouvons approximer l'équation ci-dessus par la relation linéaire suivante :

\[V_{out} \approx V_r\left(\frac{x}{4}\right)\]

Équation 2.

La figure 2 représente la sortie normalisée du pont \[\frac{V_{out}}{V_r}\] pour le cas réel (Équation 1) et la sortie idéale (Équation 2).

Figure 2. Sorties non linéaires (bleu) et idéales (rouge) des équations 1 et 2

Comme prévu, l'écart par rapport à la réponse linéaire augmente avec x.

Combien d'erreur de non-linéarité sera introduite ?

Quantifions l'erreur de non-linéarité du circuit en pont ci-dessus. Nous pouvons réécrire l'équation 1 sous la forme :

\[V_{out} =V_r \left(\frac{x}{4}\right) \left(\frac{1}{1+ \frac{x} {2}}\droit)\]

En supposant que \[\frac{x}{2} <<1\], nous pouvons utiliser le théorème de Taylor pour obtenir une approximation de la fonction ci-dessus comme :

\[V_{out} =V_r\left(\frac{x}{4}\right)\left(1 - \frac{x}{2}\right) \]

En comparant ce résultat avec l'équation 2, nous pouvons calculer l'ampleur de l'erreur comme suit :

\[E_{Non-linéarité} =V_r\left(\frac{x}{4}\right)\left(\frac{x}{2}\right) \]

En divisant cela par la valeur idéale attendue donnée par l'équation 2, nous pouvons obtenir le pourcentage d'erreur de linéarité au point final pour un changement donné de résistance (x) :

\[Pourcentage~Error =\frac{x}{2} \times 100\%\]

Exemple de calcul de l'erreur de non-linéarité

Considérons un capteur avec la réponse \[R_{sensor} =R_0(1+x)\]. Supposons que \[R_0 =100~\Omega\] et que la valeur maximale de x sur toute la plage de fonctionnement soit de 0,01. Le pourcentage d'erreur de linéarité maximum sera :

\[Pourcentage~Error =\left(\frac{0.01}{2}\right) \times 100\% =0.5\%\]

Notez que bien que nous puissions utiliser un logiciel pour supprimer les erreurs de linéarité du capteur, une réponse linéaire est souhaitable car elle augmente la précision de la mesure et facilite l'étalonnage du système. Il existe différentes topologies de circuits qui peuvent être utilisées pour linéariser les circuits en pont.

Dans la suite de cet article, nous examinerons deux techniques de linéarisation de pont différentes.

Méthode 1 :Création d'une tension proportionnelle aux changements de résistance (x)

La première technique de linéarisation que nous aborderons dans cet article est illustrée à la figure 3. Examinons d'abord l'idée de base de cette technique, puis voyons comment le circuit de la figure 3 implémente cette idée.

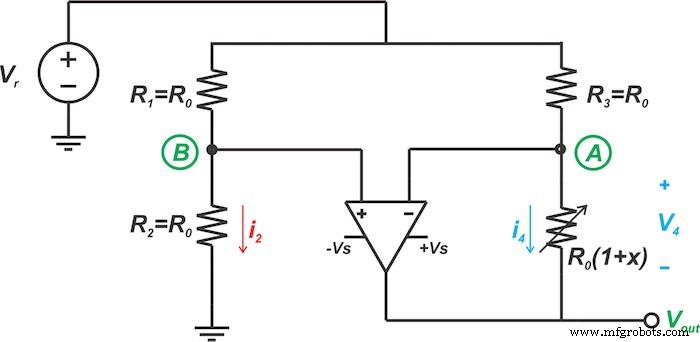
Figure 3. Un type de circuit pour linéariser les ponts de capteurs résistifs

La figure 4 montre une représentation d'un courant fixe de \[I_{Ref}\] forcé de traverser notre capteur linéaire.

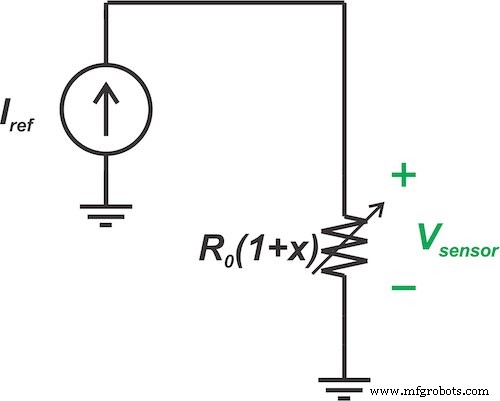
Figure 4. Un courant fixe (I_Ref ) forcé à travers un capteur linéaire

Dans ce scénario, la tension résultante aux bornes du capteur serait :

\[V_{sensor} =I_{Ref} \times R_0(1 + x)\]

qui peut être réorganisé comme :

\[V_{sensor} =R_0 \times I_{Ref} + R_0 \times I_{Ref} \times x\]

Alors que le premier terme est une valeur constante, le second terme est proportionnel aux changements de la résistance du capteur (x). Si nous pouvons omettre le terme constant, nous aurons une tension qui a une relation linéaire avec x.

Implémentation du circuit

Le circuit de la figure 3 utilise l'idée ci-dessus pour linéariser le circuit en pont. Étant donné que les entrées de l'amplificateur opérationnel ne consomment idéalement aucun courant, la tension au nœud B aura une valeur constante de :

\[v_B =\frac{R_0}{R_0 + R_0}V_r =\frac{V_r}{2}\]

La rétroaction négative ainsi que le gain élevé de l'amplificateur opérationnel forceront les entrées inverseuses et non inverseuses de l'amplificateur opérationnel à avoir la même tension :

\[v_A =v_B =\frac{V_r}{2}\]

Étant donné que les deux extrémités de R3 sont à des potentiels constants, un courant constant le traversera. En d'autres termes, l'amplificateur opérationnel fait que R3 agit comme une source de courant qui force un courant constant de \[\frac{V_r}{2R_0}\] dans le capteur. Par conséquent, la tension aux bornes du capteur sera :

\[V_4 =\frac{V_r}{2R_0} \times R_0(1 + x) =\frac{V_r}{2} + \frac{V_r}{2} x\]

Le premier terme est la valeur constante qui doit être éliminée du V_out équation. Le deuxième terme est proportionnel aux changements de résistance du capteur (x) et doit apparaître dans l'équation de sortie. En appliquant la loi de tension de Kirchhoff, on trouve V_out comme :

\[V_{out} =-V_4 + V_A =- \left(\frac{V_r}{2} + \frac{V_r}{2}x\right) + V_A\]

Par conséquent, nous n'avons besoin que de V_A être égal à \[\frac{V_r}{2}\]. Ceci est déjà satisfait, ce qui conduit à :

\[V_{out} =-\frac{V_r}{2}x\]

Par conséquent, la sortie a une relation linéaire avec x.

Méthode 2 :Création d'un courant proportionnel aux changements de résistance (x)

La deuxième technique de linéarisation de pont que nous aborderons dans cet article est illustrée à la figure 5.

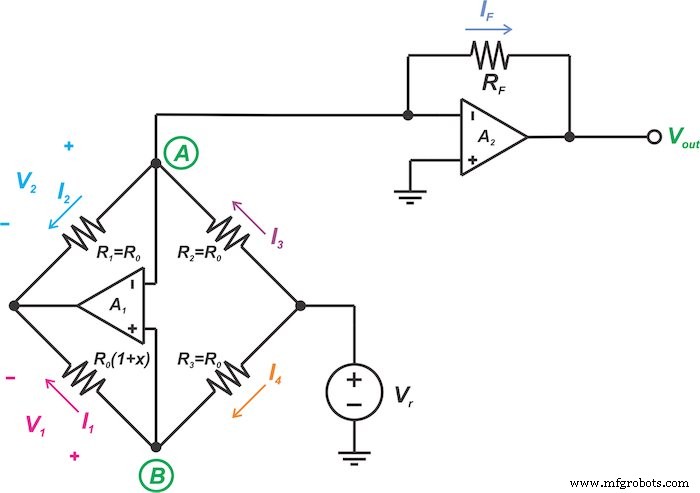
Figure 5. Un autre circuit pour la linéarisation analogique des ponts de capteurs résistifs

Jetons à nouveau un coup d'œil à l'idée de base de cette technique, puis examinons sa mise en œuvre de circuit.

Cette seconde technique de linéarisation est illustrée à la figure 6.

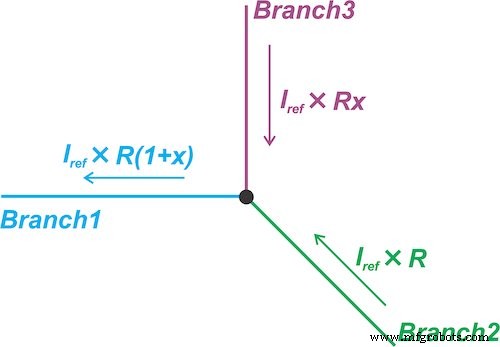
Figure 6. Technique de linéarisation forçant le courant à travers une branche du circuit à être proportionnel à la résistance du capteur

Il force le courant à travers une branche du circuit (Branche 1) à être proportionnel à la résistance du capteur :

\[I_1 =I_{Ref} \times R_0(1 + x)\]

où je_Réf est une valeur constante. Ensuite, il effectue une soustraction du domaine courant pour éliminer le terme constant \[I_{Ref} \times R_0\]. À cette fin, le courant à travers la branche 2 est défini sur \[I_{Ref} \times R_0\]. Par conséquent, le courant à travers la branche 3 sera \[I_{Ref} \times R_0x\]— proportionnel aux changements de la résistance du capteur (x).

Implémentation du circuit

Voyons comment le circuit de la figure 5 met en œuvre l'idée ci-dessus. Encore une fois, la rétroaction négative ainsi que le gain élevé des amplificateurs opérationnels forceront à la fois les entrées inverseuses et non inverseuses des deux amplificateurs opérationnels (les deux A₁ et A₂ ) pour avoir la même tension :

\[v_A =v_B =0\]

Équation 3.

Par conséquent, nous avons V₁ =V₂ qui mène à

\[R_0 (1 + x) \times I_1 =R_0 \times I_2\]

Cela se simplifie en :

\[I_2 =I_1 + I_1 \times x\]

Équation 4.

Nous savons que I₁ =I₄ et, en tenant compte de l'équation 3, nous avons :

\[I_1 =I_4 =\frac{V_r - v_A}{R_0} =\frac{V_r}{R_0}\]

En substituant ceci dans l'équation 4, nous obtenons :

\[I_2 =\frac{V_r}{R_0} + \frac{V_r}{R_0} \times x\]

Par conséquent, I₂ est la somme d'une valeur constante et d'un terme proportionnel à x. Il suffit d'utiliser la loi actuelle de Kirchhoff pour éliminer le terme constant dans l'équation du courant de sortie. Le courant à travers R2 génère un courant égal à \[\frac{V_r}{R_0}\] au nœud A, menant à :

\[I_F =-\frac{V_r}{R_0} \times x\]

On obtient donc :

\[V_{out} =V_r \times \frac{R_F}{R_0} \times x\]

Le circuit de la figure 5 a besoin d'un ampli-op supplémentaire par rapport à la première technique. Cependant, avec les deux solutions d'ampli-op, nous pouvons définir arbitrairement le gain en choisissant le rapport \[\frac{R_F}{R_0}\].

---

Pour voir une liste complète de mes articles, veuillez visiter cette page.