Architecture de réseau neuronal pour une implémentation Python

Cet article traite de la configuration Perceptron que nous utiliserons pour nos expériences avec la formation et la classification des réseaux de neurones, et nous examinerons également le sujet connexe des nœuds de biais.

Bienvenue dans la série d'articles techniques sur les réseaux de neurones All About Circuits. Jusqu'à présent, dans la série (liée ci-dessous), nous avons couvert pas mal de théories entourant les réseaux de neurones.

1. Comment effectuer une classification à l'aide d'un réseau de neurones :qu'est-ce que le perceptron ?
2. Comment utiliser un exemple simple de réseau neuronal Perceptron pour classer des données
3. Comment former un réseau de neurones Perceptron de base
4. Comprendre la formation simple sur les réseaux neuronaux
5. Une introduction à la théorie de la formation pour les réseaux de neurones
6. Comprendre le taux d'apprentissage dans les réseaux de neurones
7. Apprentissage automatique avancé avec le Perceptron multicouche
8. La fonction d'activation sigmoïde :activation dans les réseaux de neurones Perceptron multicouches
9. Comment former un réseau de neurones Perceptron multicouches
10. Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches
11. Architecture de réseau neuronal pour une implémentation Python
12. Comment créer un réseau de neurones Perceptron multicouche en Python
13. Traitement du signal à l'aide de réseaux de neurones :validation dans la conception de réseaux de neurones
14. Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Nous sommes maintenant prêts à commencer à convertir ces connaissances théoriques en un système de classification Perceptron fonctionnel.

Je veux d'abord introduire les caractéristiques générales du réseau que nous allons implémenter dans un langage de programmation de haut niveau; J'utilise Python, mais le code sera écrit de manière à faciliter la traduction vers d'autres langages tels que C. Le prochain article fournit une présentation détaillée du code Python, et après cela, nous explorerons différentes manières de s'entraîner. , en utilisant et en évaluant ce réseau.

L'architecture du réseau neuronal Python

Le logiciel correspond au Perceptron représenté dans le schéma suivant.

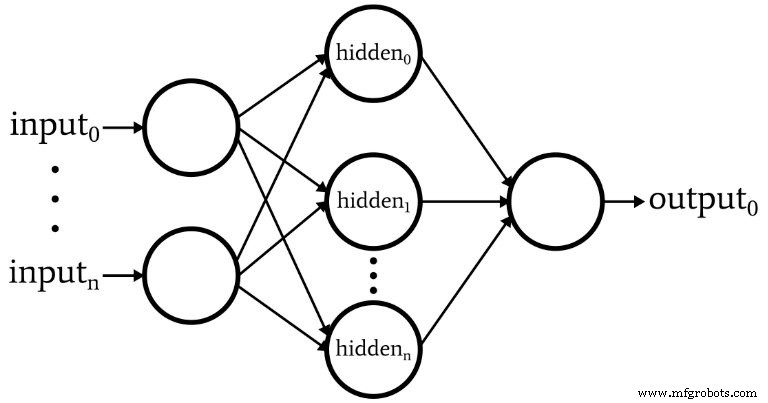
Voici les caractéristiques de base du réseau :

• Le nombre de nœuds d'entrée est variable. Ceci est essentiel si nous voulons un réseau qui a un degré de flexibilité important, car la dimensionnalité d'entrée doit correspondre à la dimensionnalité des échantillons que nous voulons classer.
• Le code ne prend pas en charge plusieurs couches cachées. À ce stade, inutile :une seule couche cachée suffit pour une classification extrêmement puissante.
• Le nombre de nœuds au sein d'une couche cachée est variable. Trouver le nombre optimal de nœuds cachés implique quelques essais et erreurs, bien qu'il existe des directives qui peuvent nous aider à choisir un point de départ raisonnable. Nous explorerons la question de la dimensionnalité des couches cachées dans un prochain article.
• Le nombre de nœuds de sortie est actuellement fixé à un. Cette limitation rendra notre programme initial un peu plus simple, et nous pouvons incorporer une dimensionnalité de sortie variable dans une version améliorée.
• La fonction d'activation pour les nœuds cachés et de sortie sera la relation sigmoïde logistique standard :

\[f(x)=\frac{1}{1+e^{-x}}\]

Qu'est-ce qu'un nœud de biais ? (AKA Bias Is Good Si vous êtes un Perceptron)

Pendant que nous discutons de l'architecture du réseau, je dois souligner que les réseaux de neurones incorporent souvent quelque chose appelé un nœud de polarisation (ou vous pouvez l'appeler simplement un "biais", sans "nœud"). La valeur numérique associée à un nœud de biais est une constante choisie par le concepteur. Par exemple :

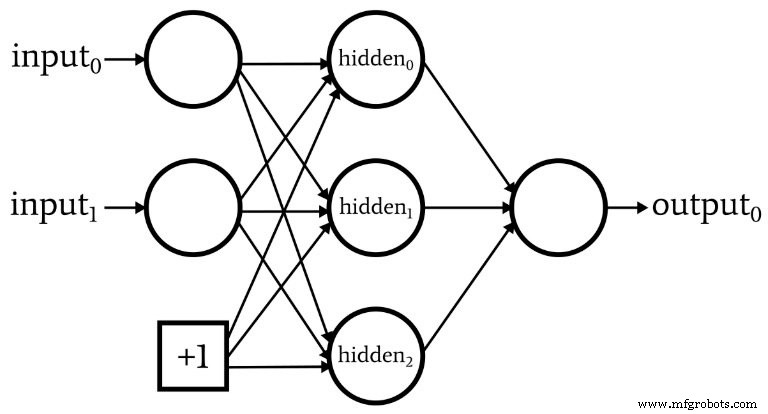
Les nœuds de polarisation peuvent être incorporés dans la couche d'entrée ou la couche cachée, ou les deux. Leurs poids sont comme tous les autres poids et sont mis à jour en utilisant la même procédure de rétropropagation.

L'utilisation de nœuds de biais est une raison importante pour écrire du code de réseau de neurones qui vous permet de modifier facilement le nombre de nœuds d'entrée ou de nœuds cachés, même si vous n'êtes intéressé que par une tâche de classification spécifique, la dimensionnalité des entrées et des couches cachées. garantit que vous pouvez facilement expérimenter l'utilisation de nœuds de biais.

Dans la partie 10, j'ai souligné que le signal de préactivation d'un nœud est calculé en effectuant un produit scalaire, c'est-à-dire que vous multipliez les éléments correspondants de deux tableaux (ou vecteurs, si vous préférez), puis additionnez tous les produits individuels. Le premier tableau contient les valeurs de postactivation de la couche précédente et le deuxième tableau contient les poids qui relient la couche précédente à la couche actuelle. Ainsi, si le tableau de postactivation de la couche précédente est noté x et le vecteur de poids est noté w, une valeur de préactivation est calculée comme suit :

\[S_{preA} =w \cdot x =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)\]

Vous vous demandez peut-être ce que cela a à voir avec les nœuds de polarisation. Eh bien, le biais (noté b) modifie cette procédure comme suit :

\[S_{preA} =( w \cdot x)+b =sum(w_1x_1 + w_2x_2 + \cdots + w_nx_n)+b\]

Un biais décale le signal qui est traité par la fonction d'activation, et il peut ainsi rendre le réseau plus flexible et robuste. L'utilisation de la lettre b pour désigner la valeur de biais rappelle l'« ordonnée à l'origine » dans l'équation standard pour une ligne droite :y =mx + b . Et ce n'est pas une pure coïncidence. Le biais est en effet comme une ordonnée à l'origine, et vous avez peut-être également remarqué que le tableau de poids équivaut à une pente :

\[S_{preA} =( w \cdot x)+b\]

\[y =mx + b\]

Poids, biais et activation

Si nous pensons aux valeurs numériques fournies à la fonction d'activation d'un nœud pendant l'entraînement, les poids augmentent ou diminuent la pente des données d'entrée et le biais décale les données d'entrée verticalement. Mais comment cela affecte-t-il la sortie du nœud ? Eh bien, supposons que nous utilisions la fonction logistique standard pour l'activation :

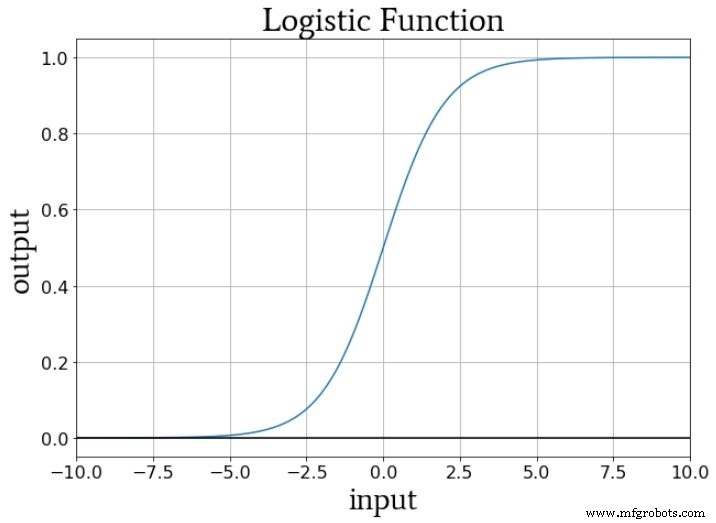
La transition de f_A (x) =0 à f_A (x) =1 est centré sur une valeur d'entrée de x =0. Ainsi, en utilisant un biais pour augmenter ou diminuer le signal de préactivation, nous pouvons influencer l'occurrence de la transition et ainsi décaler la fonction d'activation vers la gauche ou la droite . Les poids, d'autre part, déterminent à quelle « vitesse » la valeur d'entrée passe par x =0, et cela influence la pente de la transition dans la fonction d'activation.

Conclusion

Nous avons discuté des nœuds de biais et des principales caractéristiques du premier réseau de neurones que nous allons implémenter dans le logiciel. Nous sommes maintenant prêts à examiner le code réel, et c'est exactement ce que nous ferons dans le prochain article.