Alimentation dans les circuits CA résistifs et réactifs

Considérons un circuit pour un système d'alimentation CA monophasé, où une source de tension CA de 120 volts, 60 Hz fournit de l'énergie à une charge résistive :(Figure ci-dessous)

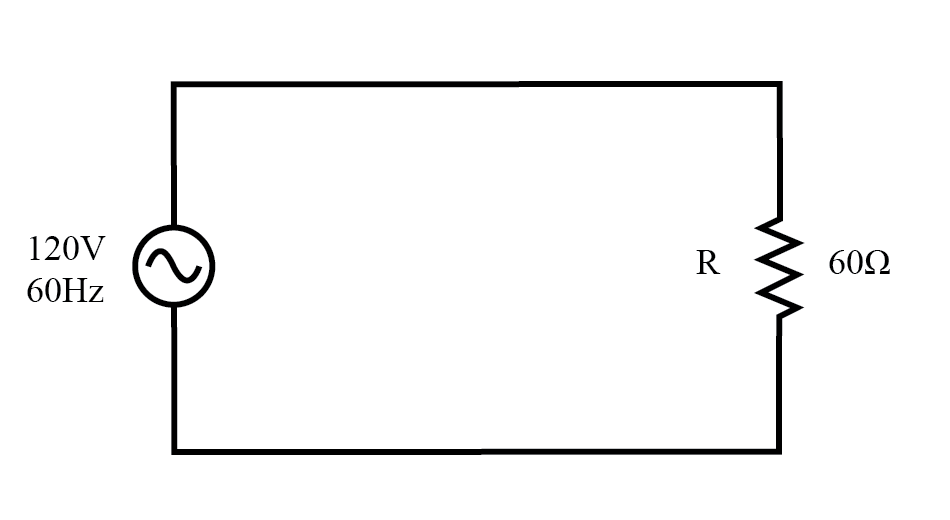
La source AC entraîne une charge purement résistive.

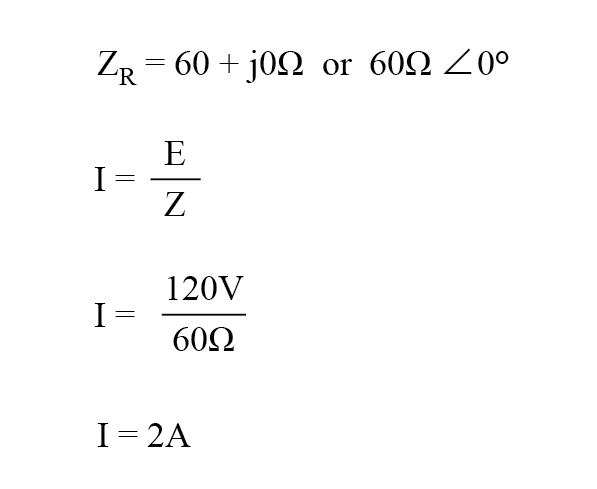
Dans cet exemple, le courant vers la charge serait de 2 ampères, RMS. La puissance dissipée à la charge serait de 240 watts.

Comme cette charge est purement résistive (pas de réactance), le courant est en phase avec la tension et les calculs ressemblent à ceux d'un circuit CC équivalent.

Si nous devions tracer les formes d'onde de tension, de courant et de puissance pour ce circuit, cela ressemblerait à la figure ci-dessous.

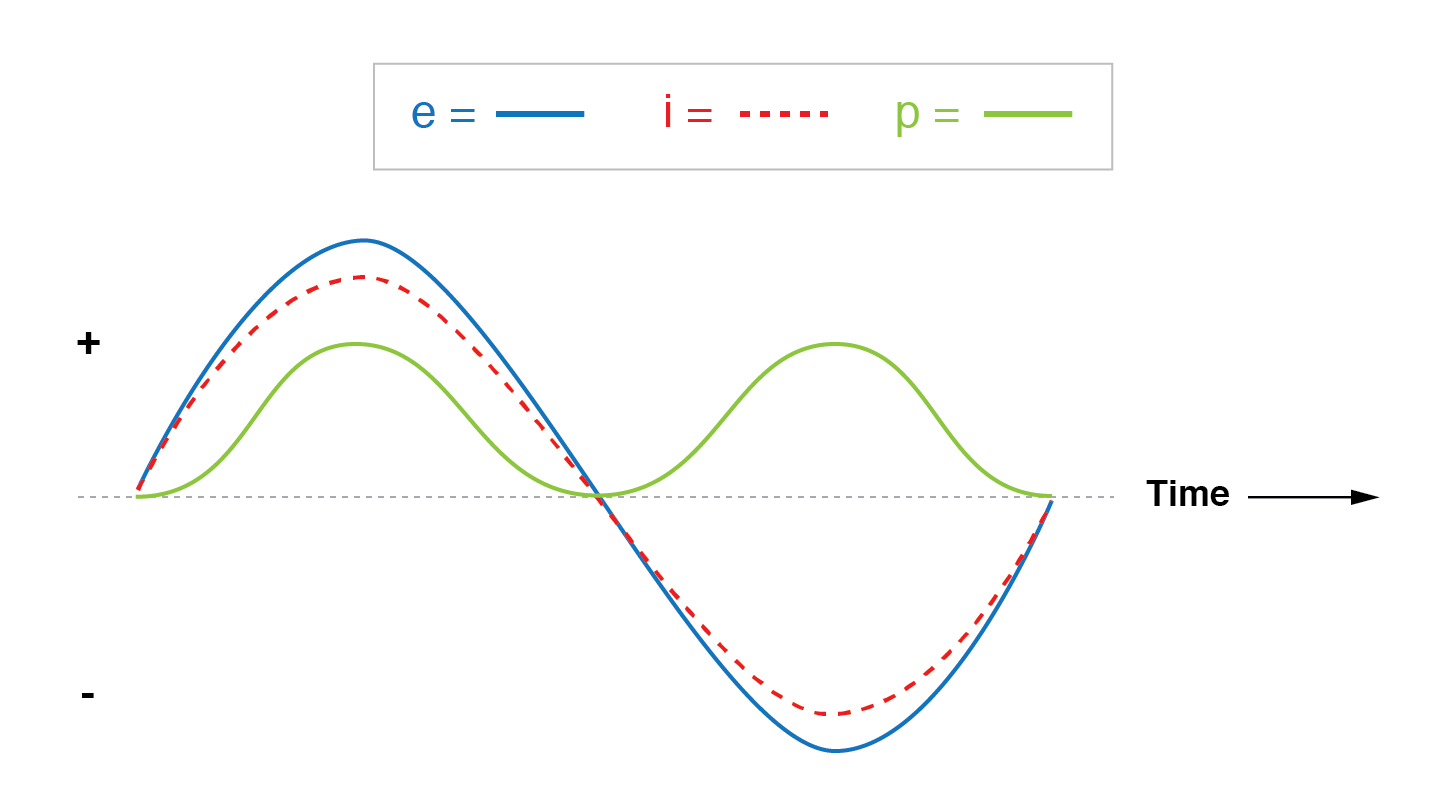
Le courant est en phase avec la tension dans un circuit résistif.

Notez que la forme d'onde de la puissance est toujours positive, jamais négative pour ce circuit résistif.

Cela signifie que la puissance est toujours dissipée par la charge résistive et n'est jamais renvoyée à la source comme c'est le cas avec les charges réactives. Si la source était un générateur mécanique, il faudrait 240 watts d'énergie mécanique (environ 1/3 de puissance) pour faire tourner l'arbre.

Notez également que la forme d'onde de la puissance n'est pas à la même fréquence que la tension ou le courant ! Au contraire, sa fréquence est double celle des formes d'onde de tension ou de courant.

Cette fréquence différente interdit notre expression de la puissance dans un circuit alternatif en utilisant la même notation complexe (rectangulaire ou polaire) que celle utilisée pour la tension, le courant et l'impédance, car cette forme de symbolisme mathématique implique des relations de phase immuables.

Lorsque les fréquences ne sont pas les mêmes, les relations de phase changent constamment.

Aussi étrange que cela puisse paraître, la meilleure façon de procéder aux calculs de puissance AC est d'utiliser scalaire notation et pour gérer toutes les relations de phase pertinentes avec la trigonométrie.

Circuit AC avec une charge purement réactive

À titre de comparaison, considérons un simple circuit CA avec une charge purement réactive dans la figure ci-dessous.

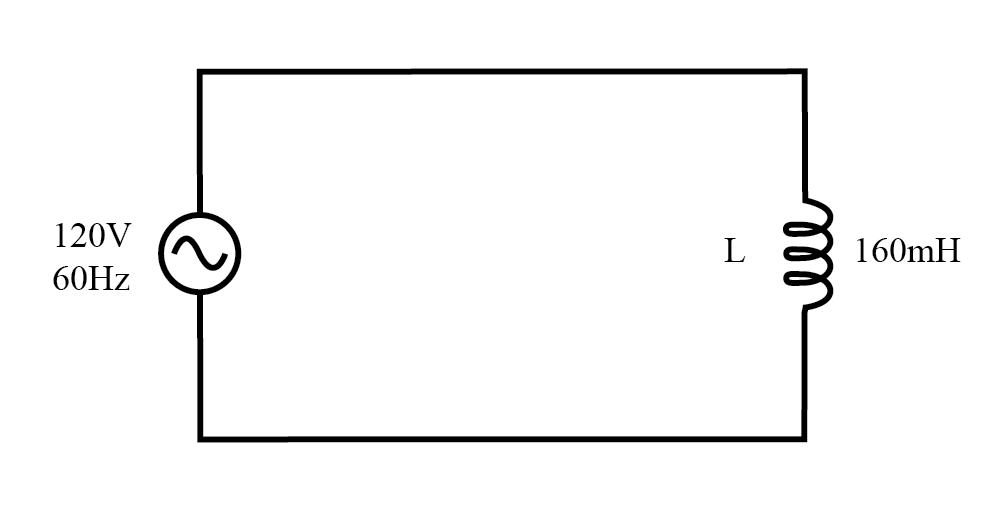
Circuit AC avec une charge purement réactive (inductive).

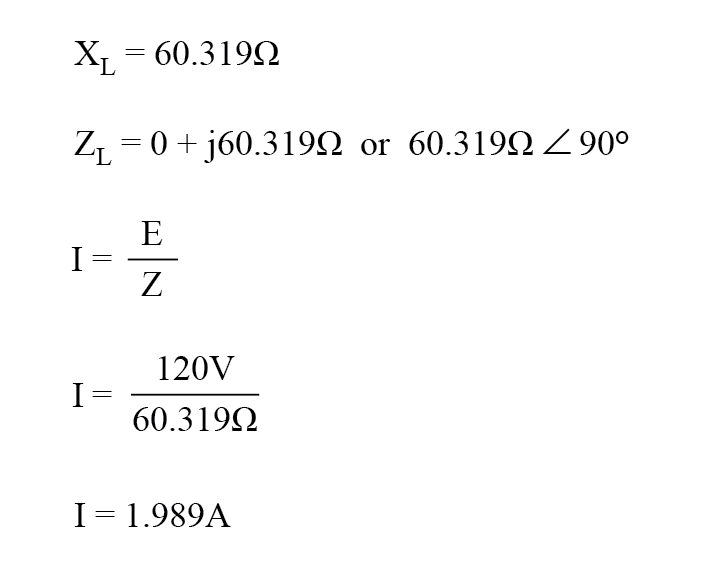
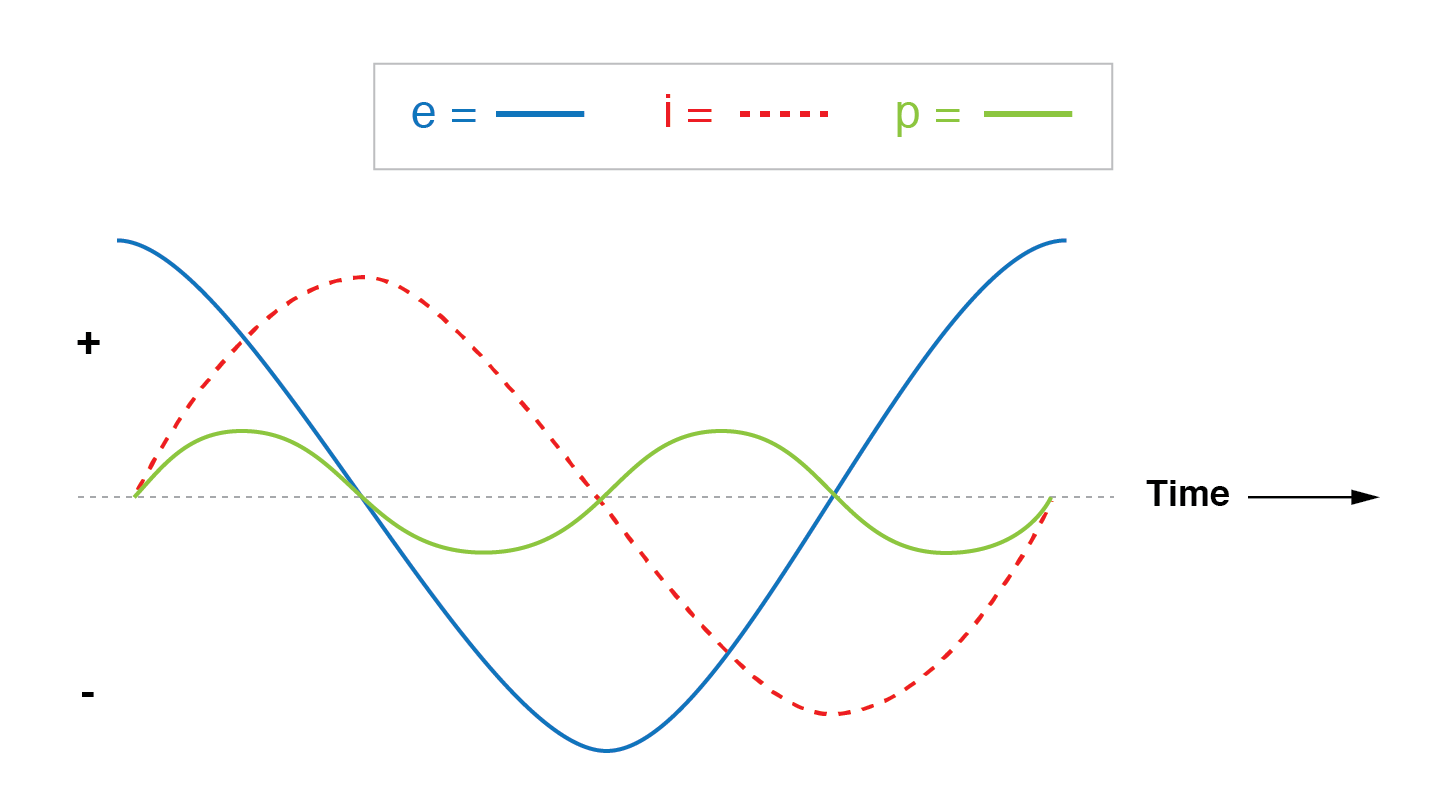
La puissance n'est pas dissipée dans une charge purement réactive. Bien qu'il soit alternativement absorbé et renvoyé à la source.

Notez que la puissance alterne également entre les cycles de positif et de négatif. (Figure ci-dessus) Cela signifie que la puissance est alternativement absorbée et renvoyée à la source.

Si la source était un générateur mécanique, il ne faudrait (pratiquement) aucune énergie mécanique nette pour faire tourner l'arbre, car aucune puissance ne serait utilisée par la charge.

L'arbre du générateur serait facile à tourner et l'inducteur ne deviendrait pas chaud comme le ferait une résistance.

Circuit AC avec une charge résistive et purement réactive

Considérons maintenant un circuit CA avec une charge composée à la fois d'inductance et de résistance dans la figure ci-dessous.

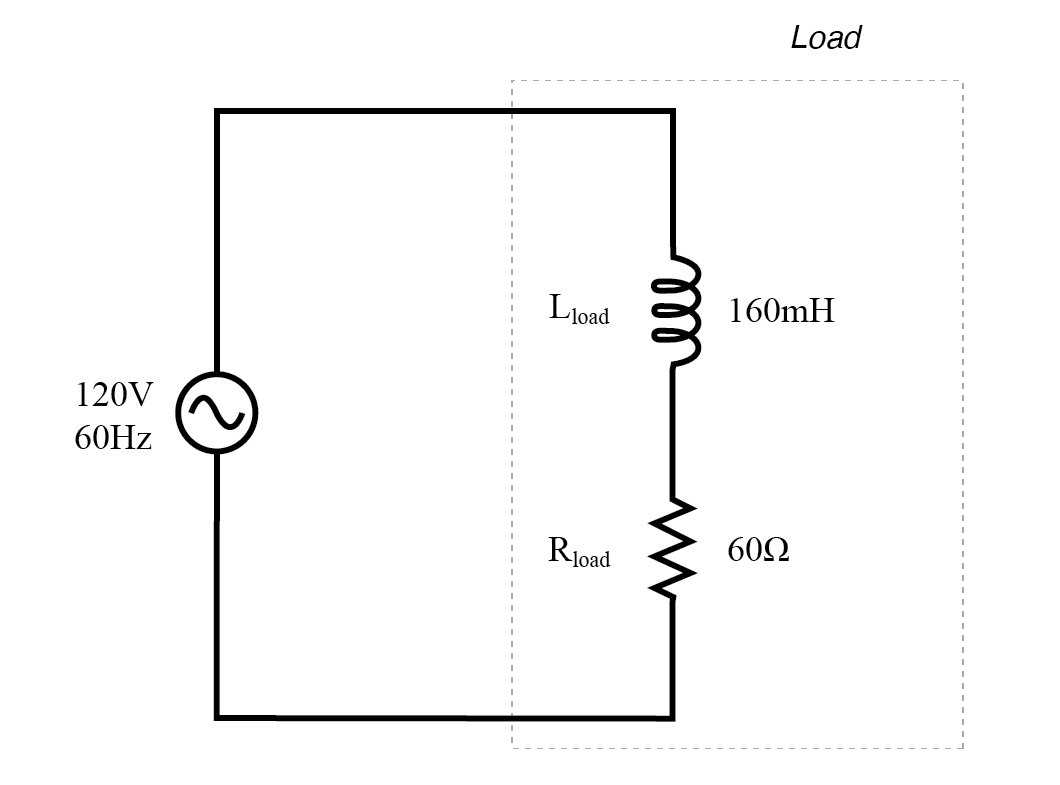
Circuit AC avec réactance et résistance.

A une fréquence de 60 Hz, les 160 millihenrys d'inductance nous donnent 60,319 Ω de réactance inductive.

Cette réactance se combine avec les 60 de résistance pour former une impédance de charge totale de 60 + j60,319 Ω, soit 85,078 Ω ∠ 45,152 ^o . Si nous ne sommes pas concernés par les angles de phase (ce que nous ne sommes pas à ce stade), nous pouvons calculer le courant dans le circuit en prenant la magnitude polaire de la source de tension (120 volts) et en la divisant par la magnitude polaire de l'impédance (85.078 Ω).

Avec une tension d'alimentation de 120 volts RMS, notre courant de charge est de 1,410 ampères. C'est le chiffre qu'un ampèremètre RMS indiquerait s'il était connecté en série avec la résistance et l'inducteur.

Nous savons déjà que les composants réactifs dissipent une puissance nulle, car ils absorbent également la puissance du reste du circuit et la renvoient au reste du circuit.

Par conséquent, toute réactance inductive dans cette charge dissipera également une puissance nulle.

La seule chose qui reste pour dissiper la puissance ici est la partie résistive de l'impédance de charge. Si nous regardons le tracé de la forme d'onde de la tension, du courant et de la puissance totale pour ce circuit, nous voyons comment cette combinaison fonctionne dans la figure ci-dessous.

Un circuit combiné résistif/réactif dissipe plus de puissance qu'il n'en renvoie à la source. La réactance ne dissipe aucune puissance; cependant, la résistance le fait.

Comme pour tout circuit réactif, la puissance alterne entre des valeurs instantanées positives et négatives au cours du temps.

Dans un circuit purement réactif, cette alternance entre la puissance positive et négative est également divisée, ce qui entraîne une dissipation de puissance nette de zéro. Cependant, dans les circuits à résistance et réactance mixtes comme celui-ci, la forme d'onde de puissance alternera toujours entre positive et négative, mais la quantité de puissance positive dépassera la quantité de puissance négative.

En d'autres termes, la charge combinée inductive/résistive consommera plus d'énergie qu'elle n'en renvoie à la source.

En regardant le tracé de la forme d'onde pour la puissance, il devrait être évident que l'onde passe plus de temps du côté positif de la ligne médiane que du côté négatif, indiquant qu'il y a plus de puissance absorbée par la charge qu'il n'en est renvoyé au circuit.

Le peu de retour de puissance qui se produit est dû à la réactance; le déséquilibre de la puissance positive par rapport à la puissance négative est dû à la résistance car elle dissipe l'énergie à l'extérieur du circuit (généralement sous forme de chaleur).

Si la source était un générateur mécanique, la quantité d'énergie mécanique nécessaire pour faire tourner l'arbre serait la quantité d'énergie moyenne entre les cycles d'alimentation positifs et négatifs.

La représentation mathématique de la puissance dans un circuit CA est un défi, car l'onde de puissance n'est pas à la même fréquence que la tension ou le courant.

De plus, l'angle de phase pour la puissance signifie quelque chose de très différent de l'angle de phase pour la tension ou le courant. Alors que l'angle pour la tension ou le courant représente un décalage relatif de synchronisation entre deux ondes, l'angle de phase pour la puissance représente un rapport entre la puissance dissipée et la puissance restituée.

En raison de cette manière dont la puissance alternative diffère de la tension ou du courant alternatif, il est en fait plus facile d'obtenir des chiffres pour la puissance en calculant avec scalaire quantités de tension, de courant, de résistance et de réactance que d'essayer de le dériver du vecteur , ou complexe quantités de tension, de courant et d'impédance avec lesquelles nous avons travaillé jusqu'à présent.

AVIS :

• Dans un circuit purement résistif, toute la puissance du circuit est dissipée par la ou les résistances. La tension et le courant sont en phase l'un avec l'autre.
• Dans un circuit purement réactif, aucune puissance du circuit n'est dissipée par la ou les charges. Au contraire, la puissance est alternativement absorbée et renvoyée à la source CA. La tension et le courant sont déphasés de 90° l'un par rapport à l'autre.
• Dans un circuit composé d'une résistance et d'une réactance mélangées, il y aura plus de puissance dissipée par la ou les charges qu'elle ne sera renvoyée, mais une certaine puissance sera certainement dissipée et une autre sera simplement absorbée et renvoyée. La tension et le courant dans un tel circuit seront déphasés d'une valeur comprise entre 0° et 90°.

FEUILLE DE TRAVAIL CONNEXE :

• Fiche de travail sur l'alimentation secteur