Atténuateurs

Qu'est-ce que les atténuateurs ?

Les atténuateurs sont des dispositifs passifs. Il est commode de les discuter avec les décibels. Les atténuateurs s'affaiblissent ou atténuent la sortie de haut niveau d'un générateur de signal, par exemple, pour fournir un signal de niveau inférieur pour quelque chose comme l'entrée d'antenne d'un récepteur radio sensible. (figure ci-dessous) L'atténuateur peut être intégré au générateur de signaux ou être un appareil autonome. Il peut fournir une quantité d'atténuation fixe ou réglable. Une section d'atténuateur peut également fournir une isolation entre une source et une charge gênante.

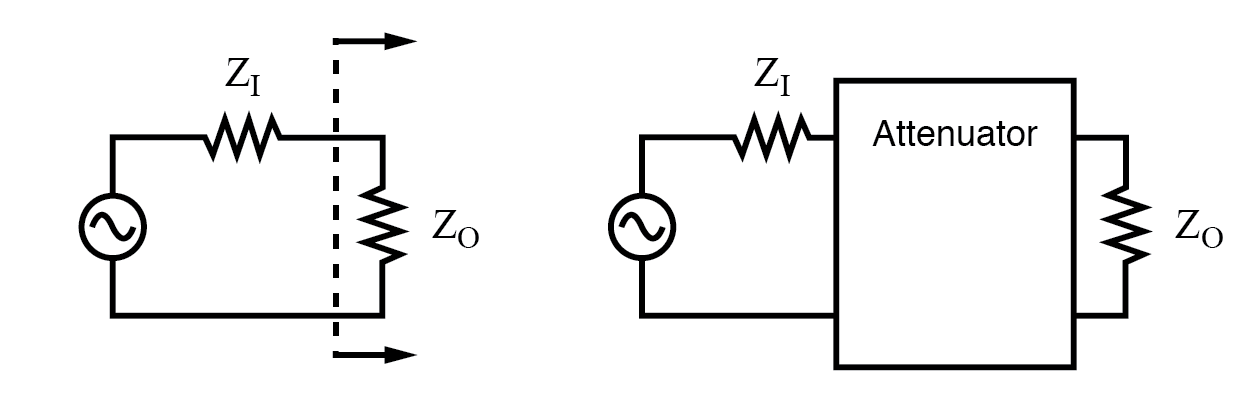
L'atténuateur à impédance constante est adapté à l'impédance de source ZI et à l'impédance de charge ZO. Pour les équipements radiofréquence, Z est de 50 Ω.

Dans le cas d'un atténuateur autonome, il doit être placé en série entre la source de signal et la charge en ouvrant le chemin du signal comme indiqué dans la figure ci-dessus. De plus, il doit correspondre à la fois à l'impédance de la source Z Je et l'impédance de charge Z O , tout en fournissant une quantité spécifiée d'atténuation. Dans cette section, nous ne considérerons que le cas particulier, et le plus courant, où les impédances de source et de charge sont égales. Non prises en compte dans cette section, des impédances de source et de charge inégales peuvent être adaptées par une section d'atténuateur. Cependant, la formulation est plus complexe.

Les atténuateurs à section en T et à section Π sont des formes courantes.

Les configurations courantes sont les T et Π réseaux illustrés dans la figure ci-dessus. Plusieurs sections d'atténuateur peuvent être mises en cascade lorsque des signaux encore plus faibles sont nécessaires, comme dans la figure ci-dessous.

Utilisation des décibels pour les atténuateurs

Les rapports de tension, tels qu'ils sont utilisés dans la conception des atténuateurs, sont souvent exprimés en décibels. Le rapport de tension doit être dérivé de l'atténuation en décibels. Les rapports de puissance exprimés en décibels sont additifs. Par exemple, un atténuateur de 10 dB suivi d'un atténuateur de 6 dB fournit 16 dB d'atténuation globale.

10 dB + 6 dB =16 dB

Les changements de niveaux sonores sont perceptibles à peu près proportionnels au logarithme du rapport de puissance (PI/PO).

niveau sonore =log10(PI / PO)

Un changement de 1 dB du niveau sonore est à peine perceptible par un auditeur, tandis que 2 dB est facilement perceptible. Une atténuation de 3dB correspond à une réduction de la puissance de moitié, tandis qu'un gain de 3dB correspond à un doublement du niveau de puissance. Un gain de -3 dB équivaut à une atténuation de +3 dB, correspondant à la moitié du niveau de puissance d'origine.

Le changement de puissance en décibels en termes de rapport de puissance est :

dB =10 log10(PI / PO)

En supposant que la charge RI à PI est la même que la résistance de charge RO à PO(RI =RO), les décibels peuvent être dérivés du rapport de tension (VI / VO) ou du rapport de courant (II / IO) :

PO =VO IO =VO2 / R =IO2 R PI =VI II =VI2 / R =II2 R dB =10 log10(PI / PO) =10 log10(VI2 / VO2) =20 log10(VI/VO) dB =10 log10(PI / PO) =10 log10(II2 / IO2) =20 log10(II/IO)

Équations en décibels

Les deux formes les plus souvent utilisées de l'équation des décibels sont :

dB =10 log10(PI / PO) ou dB =20 log10(VI / VO)

Nous utiliserons cette dernière forme, car nous avons besoin du rapport de tension. Encore une fois, la forme d'équation du rapport de tension n'est applicable que lorsque les deux résistances correspondantes sont égales. Autrement dit, la source et la résistance de charge doivent être égales.

Exemples utilisant les équations décibels

Exemple : La puissance dans un atténuateur est de 10 watts, la puissance de sortie est de 1 watt. Trouvez l'atténuation en dB.

dB =10 log10(PI / PO) =10 log10 (10 /1) =10 log10 (10) =10 (1) =10 dB

Exemple : Trouvez le rapport d'atténuation de tension (K=(VI / VO)) pour un atténuateur de 10 dB.

dB =10=20 log10(VI / VO) 10/20 =log10(VI / VO) 1010/20 =10log10(VI / VO) 3,16 =(VI / VO) =​​AP(ratio)

Exemple : La puissance dans un atténuateur est de 100 milliwatts, la puissance de sortie est de 1 milliwatt. Trouvez l'atténuation en dB.

dB =10 log10(PI / PO) =10 log10 (100 /1) =10 log10 (100) =10 (2) =20 dB

Exemple : Trouvez le rapport d'atténuation de tension (K=(VI / VO)) pour un atténuateur de 20 dB.

dB =20=20 log10(VI / VO ) 1020/20 =10 log10(VI / VO ) 10 =(VI / VO ) =K

Atténuateur de section en T

Les atténuateurs T et Π doivent être connectés à un Z source et Z impédance de charge. Le Z -(flèches) pointant vers l'extérieur de l'atténuateur dans la figure ci-dessous l'indiquent. Le Z -(flèches) pointant vers l'atténuateur indique que l'impédance vue en regardant dans l'atténuateur avec une charge Z à l'extrémité opposée est Z, Z=50 Ω pour notre cas. Cette impédance est une constante (50 Ω) par rapport à l'atténuation - l'impédance ne change pas lorsque l'atténuation est modifiée.

Le tableau de la figure ci-dessous répertorie les valeurs de résistance pour le T et Π atténuateurs pour correspondre à une source/charge de 50 Ω, comme c'est l'exigence habituelle dans le travail de radiofréquence.

Les services téléphoniques et autres travaux audio nécessitent souvent une correspondance à 600 Ω. Multipliez tous les R valeurs par le rapport (600/50) pour corriger la correspondance de 600 . Multiplier par 75/50 convertirait les valeurs de la table pour correspondre à une source et à une charge de 75 .

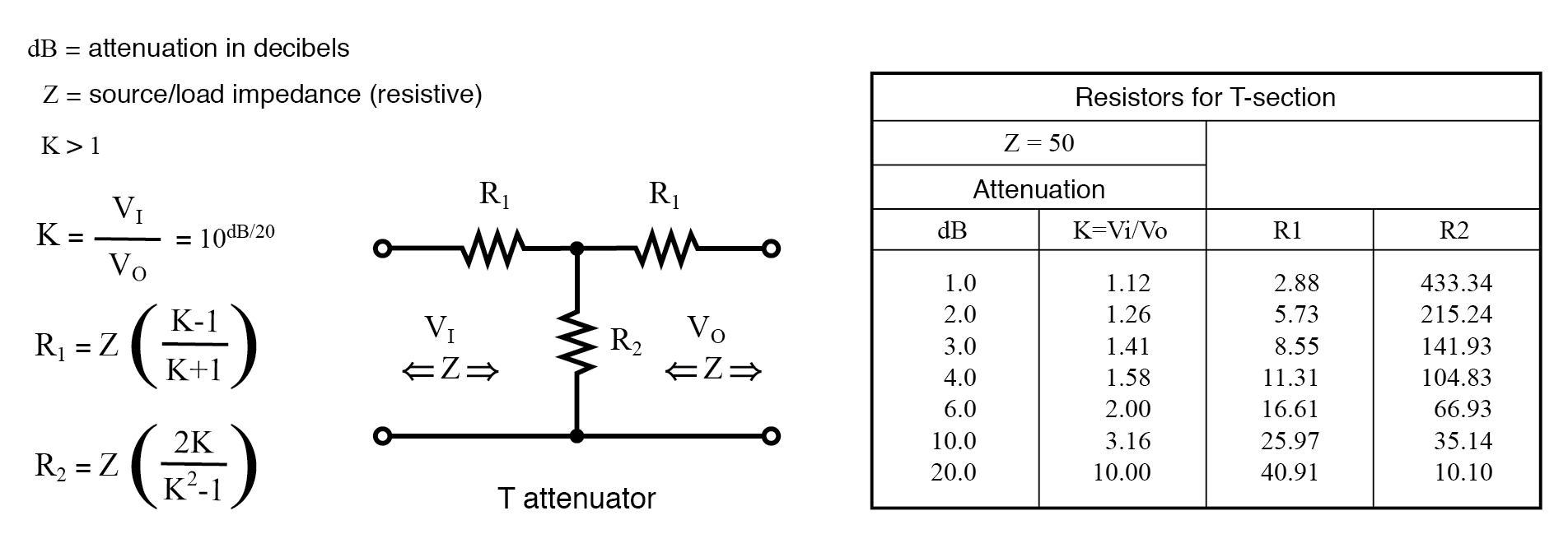
Formules pour les résistances d'atténuateur de section en T, étant donné K, le rapport d'atténuation de tension et ZI =ZO =50 Ω.

La quantité d'atténuation est habituellement spécifiée en dB (décibels). Cependant, nous avons besoin du rapport de tension (ou de courant) K pour trouver les valeurs de résistance à partir d'équations. Voir le dB/20 terme au pouvoir de 10 terme pour calculer le rapport de tension K à partir de dB, ci-dessus.

Le T (et ci-dessous Π ) les configurations sont les plus couramment utilisées car elles fournissent une correspondance bidirectionnelle. C'est-à-dire que l'entrée et la sortie de l'atténuateur peuvent être échangées bout à bout et toujours correspondre aux impédances de la source et de la charge tout en fournissant la même atténuation.

Déconnecter la source et regarder à droite sur V Je , nous devons voir une combinaison parallèle en série de R 1 , R 2 , R 1 , et Z ressemblant à une résistance équivalente de Z EN , la même que l'impédance source/charge Z :(une charge de Z est connectée à la sortie.)

ZIN =R1 + (R2 ||(R1 + Z))

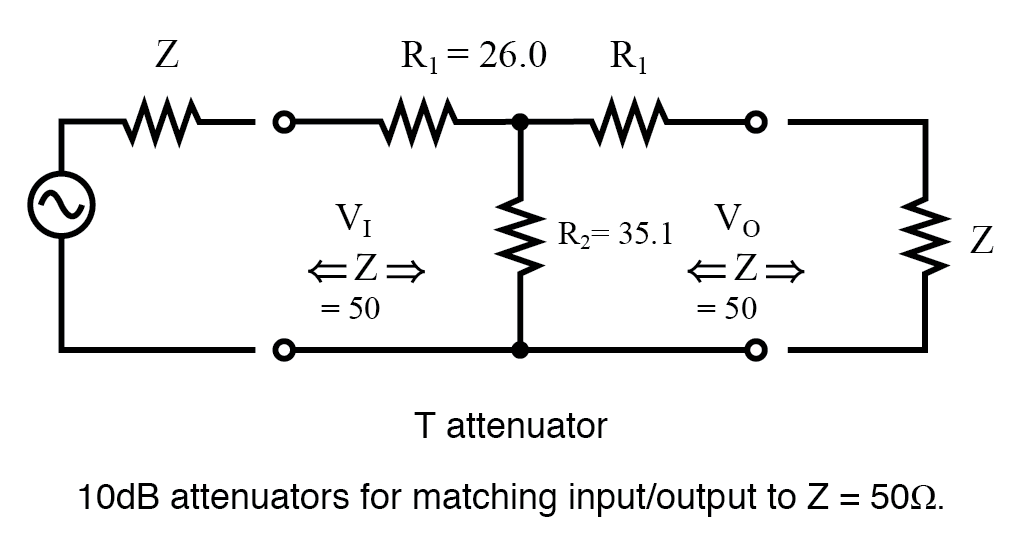
Par exemple, remplacez les valeurs de 10 dB du tableau des atténuateurs 50  par R 1 et R 2 comme le montre la figure ci-dessous.

ZIN =25,97 + (35,14 ||(25,97 + 50)) ZIN =25,97 + (35,14 || 75,97 ) ZIN =25,97 + 24,03 =50

Cela nous montre que nous voyons 50 en regardant droit dans l'exemple d'atténuateur (figure ci-dessous) avec une charge de 50 Ω.

Remplacement du générateur de source, déconnexion de la charge Z à V O , et en regardant vers la gauche, devrait nous donner la même équation que ci-dessus pour l'impédance à V O , en raison de la symétrie. De plus, les trois résistances doivent être des valeurs qui fournissent l'atténuation requise de l'entrée à la sortie. Ceci est accompli par les équations pour R 1 et R 2 ci-dessus tel qu'appliqué au T -atténuateur ci-dessous.

Atténuateur de section PI

Le tableau de la figure ci-dessous répertorie les valeurs de résistance pour le Π atténuateur correspondant à une source/charge de 50 à certains niveaux d'atténuation courants. Les résistances correspondant à d'autres niveaux d'atténuation peuvent être calculées à partir des équations.

Formules pour les résistances d'atténuateur de section Π, étant donné K, le rapport d'atténuation de tension, et ZI =ZO =50 Ω.

Ce qui précède s'applique à l'atténuateur ci-dessous.

Quelles valeurs de résistance seraient requises pour le Π atténuateurs pour 10 dB d'atténuation correspondant à une source et une charge de 50  ?

Exemple d'atténuateur de section Π de 10 dB pour faire correspondre une source et une charge de 50 Ω.

Le 10 dB correspond à un rapport d'atténuation de tension de K=3.16 à l'avant-dernière ligne du tableau ci-dessus. Transférez les valeurs de résistance de cette ligne vers les résistances du schéma de la figure ci-dessus.

Atténuateur de section en L

Le tableau de la figure ci-dessous répertorie les valeurs de résistance pour le L atténuateurs pour correspondre à une source/charge de 50 . Le tableau de la figure ci-dessous répertorie également les valeurs de résistance pour une forme alternative. Notez que les valeurs de résistance ne sont pas les mêmes.

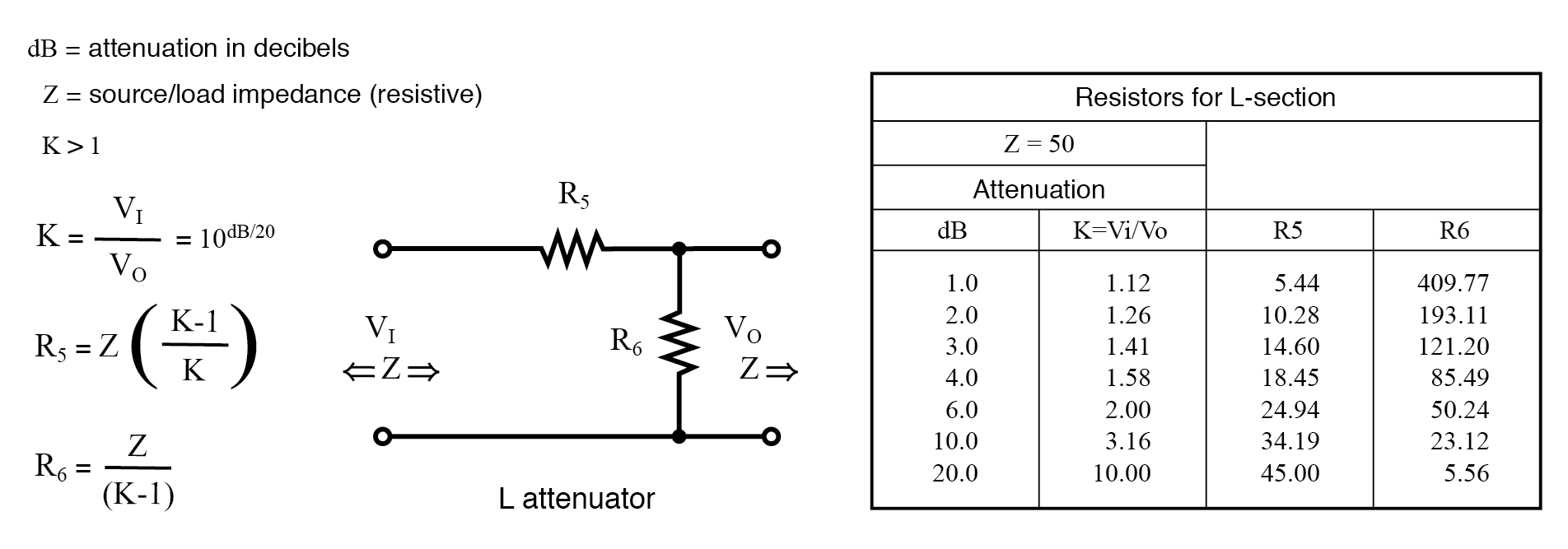
Tableau des atténuateurs en L pour une impédance de source et de charge de 50 .

Ce qui précède s'applique au L atténuateur ci-dessous.

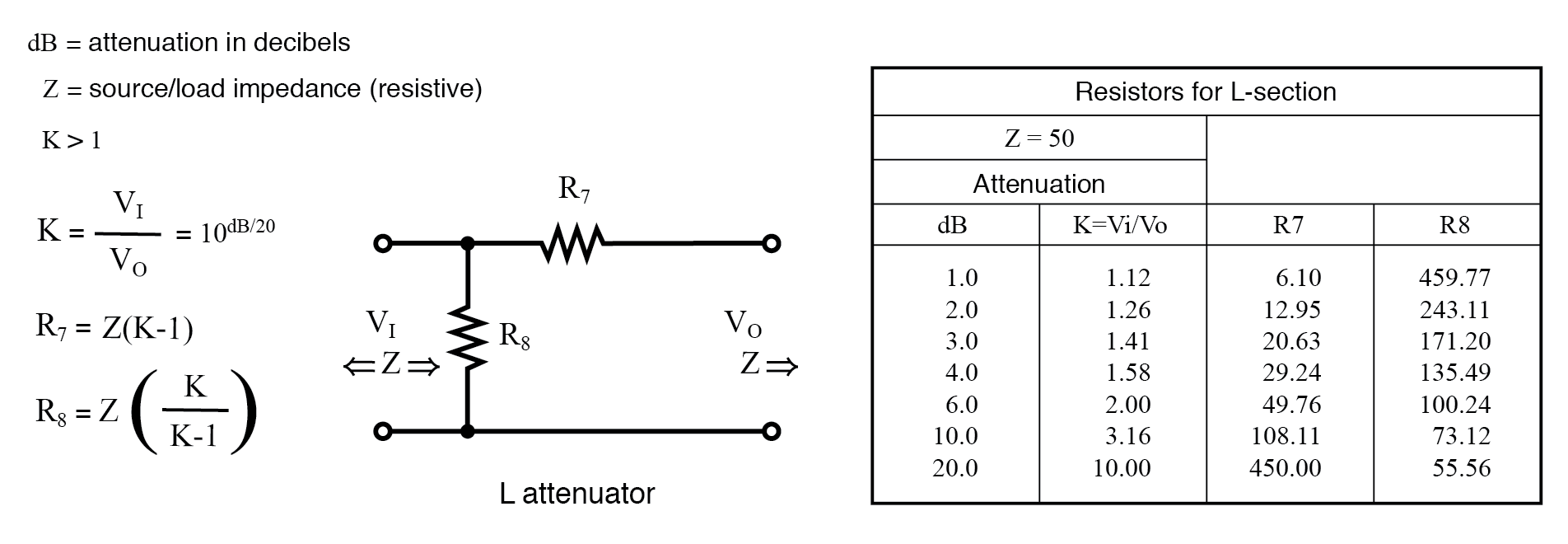
Tableau des atténuateurs à section en L de forme alternative pour une impédance de source et de charge de 50 .

Atténuateur ponté en T

Le tableau de la figure ci-dessous répertorie les valeurs de résistance pour le T ponté atténuateurs pour correspondre à une source et à une charge de 50 . L'atténuateur ponté en T n'est pas souvent utilisé. Pourquoi pas ?

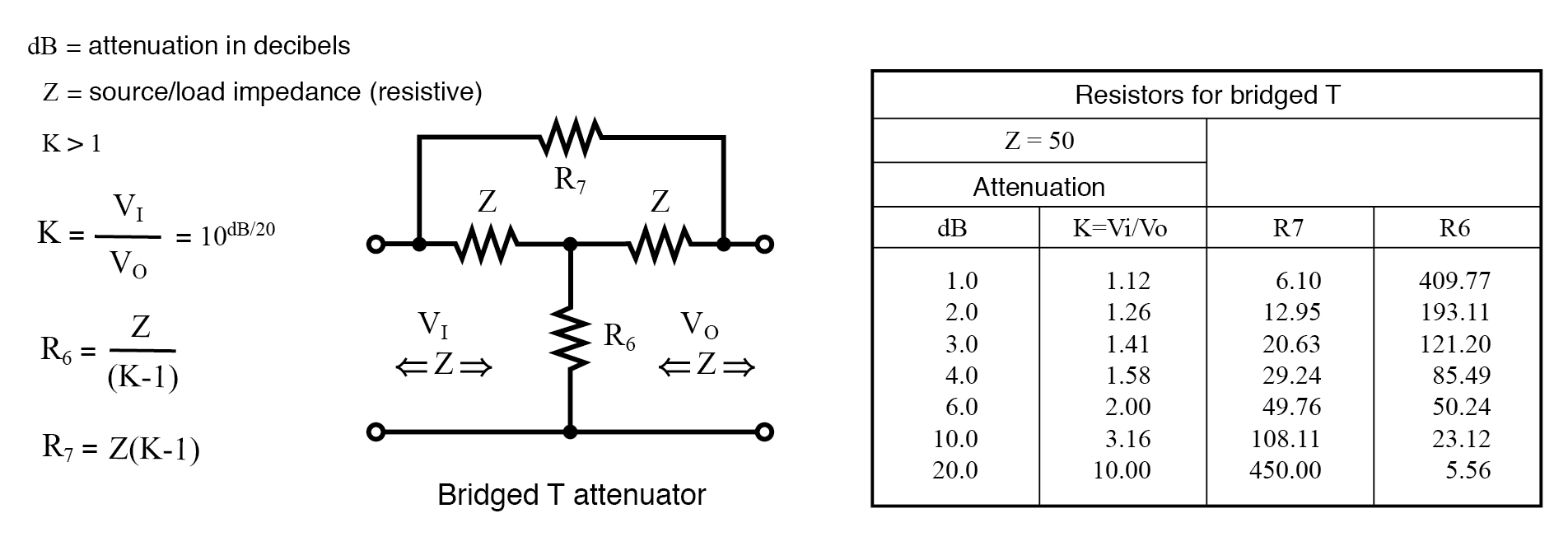
Formules et tableau abrégé pour section atténuateur ponté en T, Z =50 Ω.

Sections en cascade

Les sections d'atténuateur peuvent être mises en cascade comme dans la figure ci-dessous pour plus d'atténuation que ce qui peut être disponible à partir d'une seule section. Par exemple, deux atténuateurs de 10 dB peuvent être montés en cascade pour fournir 20 dB d'atténuation, les valeurs de dB étant additives. Le rapport d'atténuation de tension K ou V Je /V O pour une section d'atténuateur de 10 dB est de 3,16. Le rapport d'atténuation de tension pour les deux sections en cascade est le produit des deux K s ou 3,16x3,16=10 pour les deux sections en cascade.

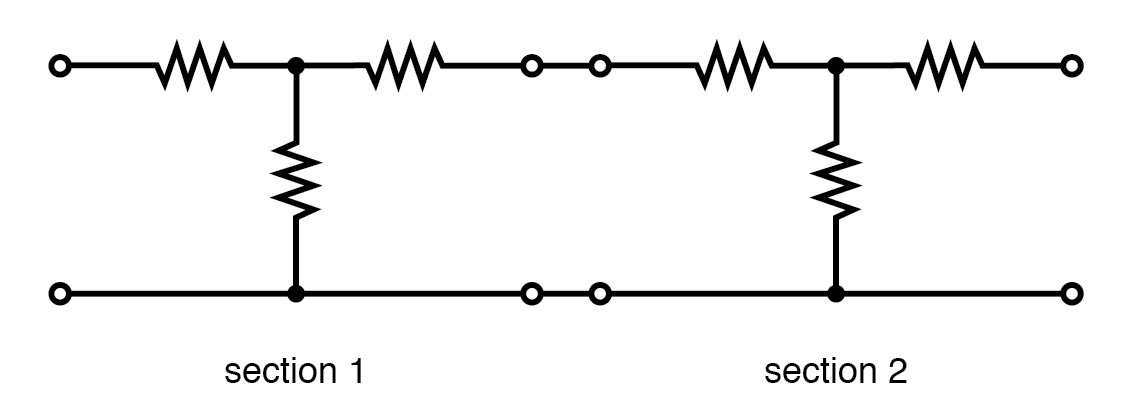
Sections d'atténuateur en cascade :l'atténuation en dB est additive.

Une atténuation variable peut être fournie par étapes discrètes par un atténuateur commuté. L'exemple de la figure ci-dessous, montré dans la position 0 dB, est capable de 0 à 7 dB d'atténuation par commutation additive d'aucune, d'une ou de plusieurs sections.

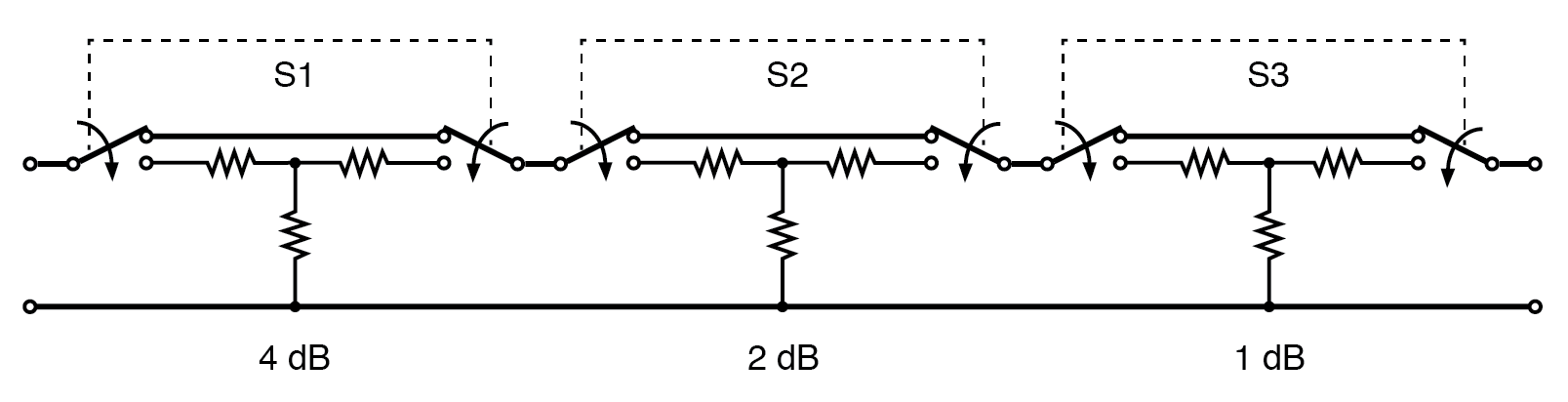
Atténuateur commuté :l'atténuation est variable par paliers discrets.

L'atténuateur multi-sections typique a plus de sections que la figure ci-dessus ne le montre. L'ajout d'une section de 3 ou 8 dB au-dessus permet à l'unité de couvrir jusqu'à 10 dB et au-delà. Des niveaux de signal inférieurs sont obtenus par l'ajout de sections de 10 dB et 20 dB, ou d'une section binaire multiple de 16 dB.

Atténuateurs RF

Pour les travaux en radiofréquence (RF) (<1000 Mhz), les sections individuelles doivent être montées dans des compartiments blindés pour contrecarrer le couplage capacitif si des niveaux de signal inférieurs doivent être atteints aux fréquences les plus élevées. Les sections individuelles des atténuateurs commutés de la section précédente sont montées dans des sections blindées. Des mesures supplémentaires peuvent être prises pour étendre la gamme de fréquences au-delà de 1000 MHz. Cela implique une construction à partir d'éléments résistifs sans plomb de forme spéciale.

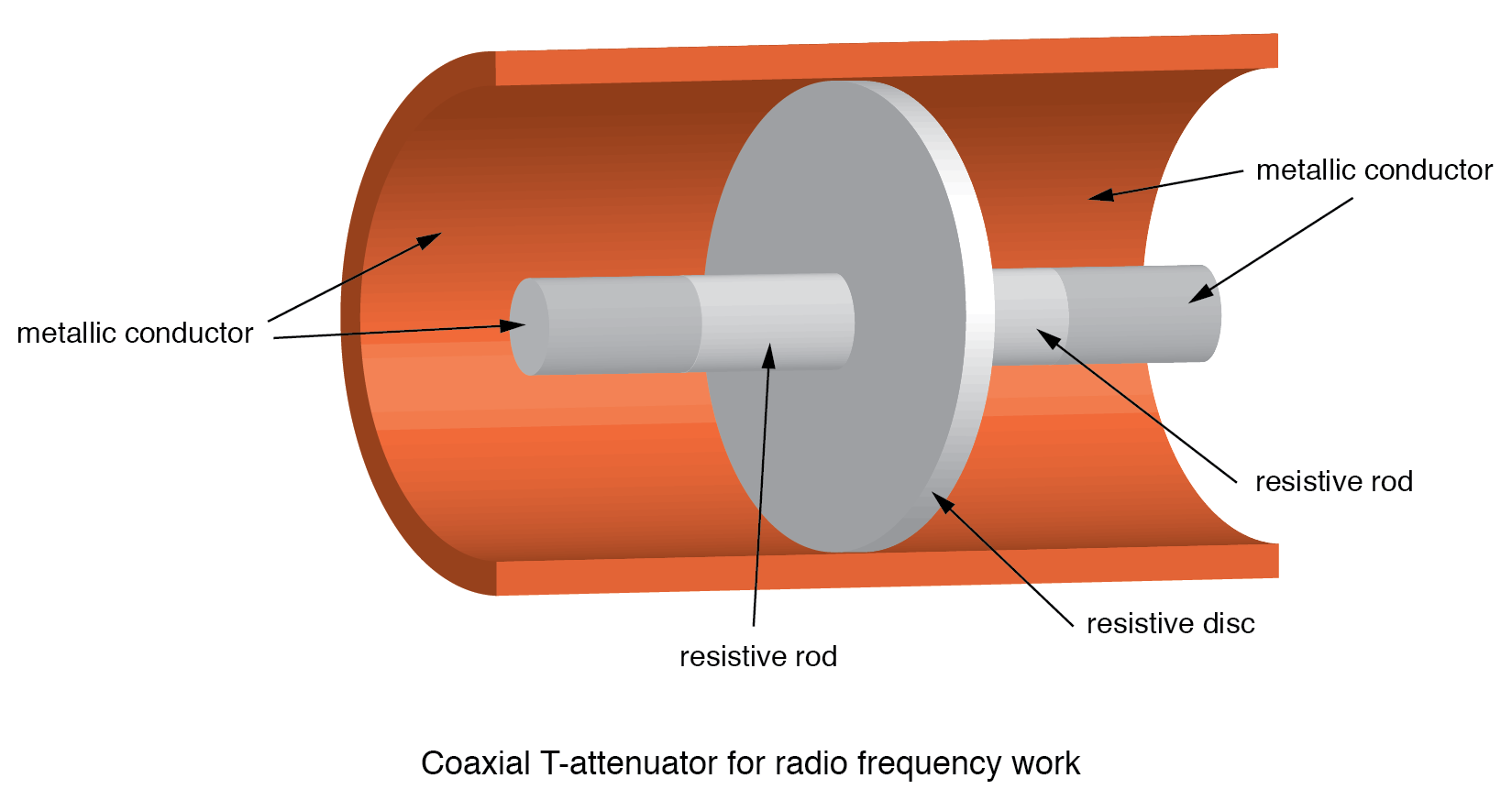
Un atténuateur coaxial à section en T composé de tiges résistives et d'un disque résistif est illustré dans la figure ci-dessus. Cette construction est utilisable à quelques gigahertz. La version coaxiale aurait une tige résistive entre deux disques résistifs dans la ligne coaxiale comme dans la figure ci-dessous.

Des connecteurs RF, non représentés, sont fixés aux extrémités des atténuateurs T et ci-dessus. Les connecteurs permettent de mettre en cascade des atténuateurs individuels, en plus de la connexion entre une source et une charge. Par exemple, un atténuateur de 10 dB peut être placé entre une source de signal problématique et une entrée d'analyseur de spectre coûteuse. Même si nous n'avons peut-être pas besoin de l'atténuation, l'équipement de test coûteux est protégé de la source en atténuant toute surtension.

Résumé :Atténuateurs

• Un atténuateur réduit un signal d'entrée à un niveau inférieur.
• La quantité d'atténuation est spécifiée en décibels (dB). Les valeurs en décibels s'additionnent pour les sections d'atténuateur en cascade.
• dB à partir du rapport de puissance :dB = 10 log10(PI/PO)
• dB à partir du rapport de tension :dB =20 log10(VI / VO)
• T et Π les atténuateurs de section sont les configurations de circuit les plus courantes.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les mesures des décibels