Considérations pratiques des circuits ADC

Peut-être que la considération la plus importante d'un ADC est sa résolution . La résolution est le nombre de bits binaires émis par le convertisseur. Étant donné que les circuits ADC reçoivent un signal analogique, qui est variable en continu, et le résolvent en l'une des nombreuses étapes discrètes, il est important de savoir combien de ces étapes il y a au total.

Par exemple, un CAN avec une sortie 10 bits peut représenter jusqu'à 1024 (2 ¹⁰ ) conditions uniques de mesure du signal. Sur la plage de mesure de 0% à 100%, il y aura exactement 1024 nombres binaires uniques produits par le convertisseur (de 0000000000 à 1111111111, inclus).

Un CAN 11 bits aura deux fois plus d'états à sa sortie (2048, soit 2 ¹¹ ), représentant deux fois plus de conditions uniques de mesure de signal entre 0 % et 100 %.

La résolution est très importante dans les systèmes d'acquisition de données (circuits conçus pour interpréter et enregistrer des mesures physiques sous forme électronique). Supposons que nous mesurions la hauteur d'eau dans un réservoir de stockage de 40 pieds de haut à l'aide d'un instrument avec un CAN 10 bits.

0 pied d'eau dans le réservoir correspond à 0% de la mesure, tandis que 40 pieds d'eau dans le réservoir correspond à 100% de la mesure. Étant donné que l'ADC est fixé à 10 bits de sortie de données binaires, il interprétera tout niveau de réservoir donné comme l'un des 1024 états possibles.

Pour déterminer le niveau d'eau physique qui sera représenté dans chaque étape de l'ADC, nous devons diviser la plage de mesure de 40 pieds par le nombre de pas dans la plage de possibilités de 0 à 1024, qui est de 1023 (un de moins que 1024). En faisant cela, nous obtenons un chiffre de 0,039101 pied par pas.

Cela équivaut à 0,46921 pouces par pas, un peu moins d'un demi-pouce de niveau d'eau représenté pour chaque compte binaire de l'ADC.

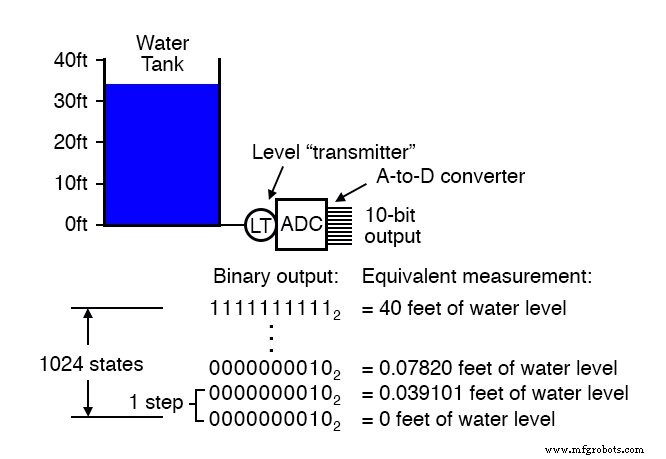
Cette valeur de pas de 0,039101 pieds (0,46921 pouces) représente la plus petite quantité de changement de niveau du réservoir détectable par l'instrument. Certes, il s'agit d'une petite quantité, moins de 0,1% de la plage de mesure globale de 40 pieds.

Cependant, pour certaines applications, cela peut ne pas être assez fin. Supposons que nous ayons besoin de cet instrument pour pouvoir indiquer les changements de niveau du réservoir jusqu'à un dixième de pouce. Afin d'atteindre ce degré de résolution tout en conservant une étendue de mesure de 40 pieds, nous aurions besoin d'un instrument avec plus de dix bits ADC.

Pour déterminer combien de bits ADC sont nécessaires, nous devons d'abord déterminer combien de pas de 1/10 de pouce il y a dans 40 pieds. La réponse à cela est 40/(0,1/12), ou 4800 pas de 1/10 de pouce sur 40 pieds. Ainsi, nous avons besoin de suffisamment de bits pour fournir au moins 4800 pas discrets dans une séquence de comptage binaire.

10 bits nous ont donné 1023 pas, et nous le savions en calculant 2 à la puissance 10 (2 ¹⁰ =1024) puis en soustrayant un.

En suivant la même procédure mathématique, 2 ¹¹ -1 =2047, 2 ¹² -1 =4095, et 2 ¹³ -1 =8191. 12 bits sont inférieurs à la quantité nécessaire pour 4800 pas, tandis que 13 bits sont plus que suffisants. Par conséquent, nous avons besoin d'un instrument avec au moins 13 bits de résolution.

Une autre considération importante des circuits ADC est sa fréquence d'échantillonnage , ou taux de conversion .

Il s'agit simplement de la vitesse à laquelle le convertisseur sort un nouveau nombre binaire. Comme la résolution, cette considération est liée à l'application spécifique de l'ADC. Si le convertisseur est utilisé pour mesurer des signaux à changement lent tels que le niveau dans un réservoir de stockage d'eau, il pourrait probablement avoir une fréquence d'échantillonnage très lente et toujours fonctionner correctement.

A l'inverse, s'il est utilisé pour numériser un signal de fréquence audio cyclique à plusieurs milliers de fois par seconde, le convertisseur doit être considérablement plus rapide. Considérez l'illustration suivante du taux de conversion du CAN par rapport au type de signal, typique d'un CAN à approximations successives avec des intervalles d'échantillonnage réguliers :

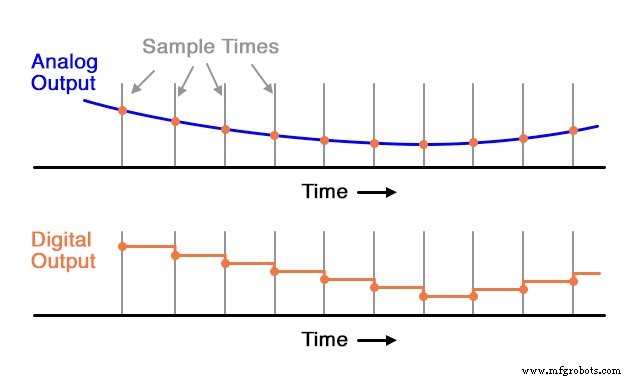
Ici, pour ce signal à évolution lente, la fréquence d'échantillonnage est plus que suffisante pour capturer sa tendance générale. Mais considérez ceci exemple avec le même temps d'échantillonnage :

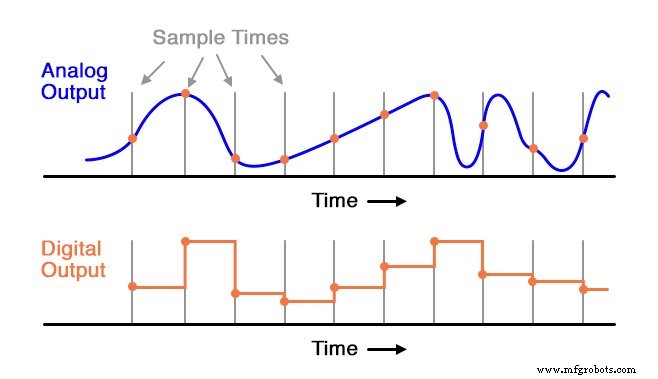
Lorsque la période d'échantillonnage est trop longue (trop lente), des détails substantiels du signal analogique seront manqués. Remarquez comment, en particulier dans les dernières parties du signal analogique, la sortie numérique ne parvient absolument pas à reproduire la vraie forme.

Même dans la première section de la forme d'onde analogique, la reproduction numérique s'écarte sensiblement de la forme réelle de l'onde. Il est impératif que le temps d'échantillonnage d'un CAN soit suffisamment rapide pour capturer les changements essentiels dans la forme d'onde analogique.

Dans la terminologie d'acquisition de données, la forme d'onde à la fréquence la plus élevée qu'un CAN peut théoriquement capturer est la soi-disant fréquence de Nyquist , égal à la moitié de la fréquence d'échantillonnage du CAN. Par conséquent, si un circuit ADC a une fréquence d'échantillonnage de 5000 Hz, la forme d'onde à la fréquence la plus élevée qu'il peut résoudre avec succès sera la fréquence de Nyquist de 2500 Hz.

Si un CAN est soumis à un signal d'entrée analogique dont la fréquence dépasse la fréquence de Nyquist pour ce CAN, le convertisseur produira un signal numérisé de fréquence faussement basse. Ce phénomène est connu sous le nom d'aliasing . Observez l'illustration suivante pour voir comment l'alias se produit :

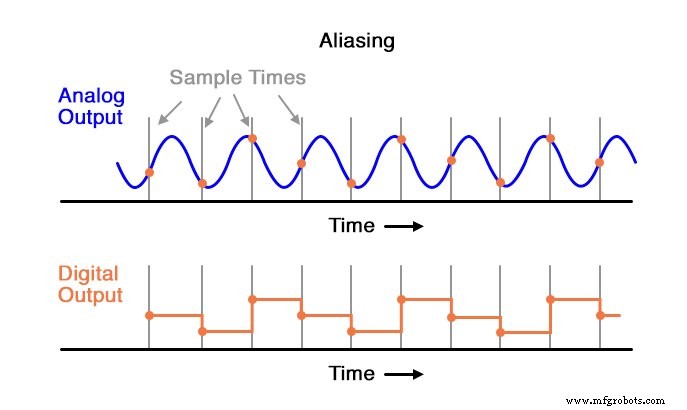
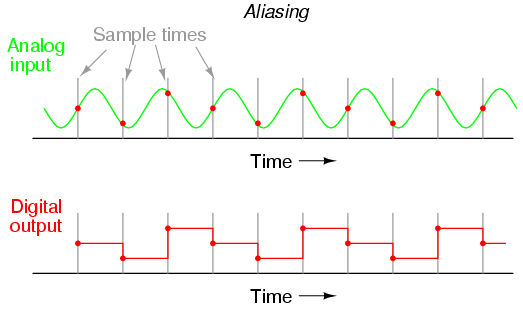
Notez que la période de la forme d'onde de sortie est beaucoup plus longue (plus lente) que celle de la forme d'onde d'entrée et que les deux formes d'onde ne sont même pas similaires :

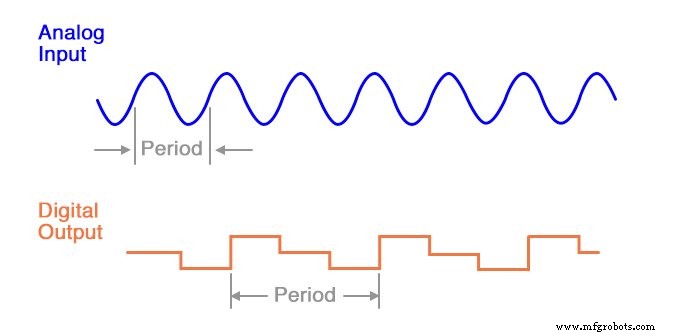
Il faut comprendre que la fréquence de Nyquist est un absolu limite de fréquence maximale pour un CAN et ne représente pas la plus haute pratique fréquence mesurable. Pour plus de sécurité, il ne faut pas s'attendre à ce qu'un CAN résolve avec succès une fréquence supérieure à un cinquième à un dixième de sa fréquence d'échantillonnage.

Un moyen pratique d'empêcher l'aliasing est de placer un filtre passe-bas avant l'entrée de l'ADC, pour bloquer toute fréquence de signal supérieure à la limite pratique. De cette façon, le circuit ADC sera empêché de voir des fréquences excessives et n'essaiera donc pas de les numériser.

Il est généralement préférable que de telles fréquences ne soient pas converties que de les faire "créneler" et apparaître dans la sortie comme de faux signaux.

Une autre mesure des performances de l'ADC est ce qu'on appelle la récupération par étapes . Il s'agit d'une mesure de la rapidité avec laquelle un CAN modifie sa sortie pour correspondre à un changement important et soudain de l'entrée analogique. Dans certaines technologies de convertisseur en particulier, la récupération d'étape est une limitation sérieuse.

Un exemple est le convertisseur de suivi, qui a une période de mise à jour généralement rapide mais une récupération de pas disproportionnellement lente. Un ADC idéal a un grand nombre de bits pour une résolution très fine, échantillonne à des vitesses ultra-rapides et récupère instantanément les étapes. Il n'existe malheureusement pas non plus dans le monde réel.

Bien sûr, n'importe lequel de ces traits peut être amélioré grâce à une complexité de circuit supplémentaire, soit en termes d'augmentation du nombre de composants et/ou de conceptions de circuits spéciaux conçus pour fonctionner à des vitesses d'horloge plus élevées.

Différentes technologies ADC, cependant, ont des points forts différents. Voici un résumé d'entre eux classés du meilleur au pire :

• Rapport résolution/complexité : Intégration simple pente, intégration double pente, compteur, suivi, approximation successive, flash.
• Vitesse : Flash, suivi, approximation successive, intégration et compteur à pente unique, intégration à double pente.
• Récupération d'étape : Flash, approximation successive, intégration et compteur à pente unique, intégration à double pente, suivi. Veuillez garder à l'esprit que le classement de ces différentes technologies ADC dépend d'autres facteurs.

Par exemple, la façon dont un ADC évalue la récupération de pas dépend de la nature du changement de pas. Un ADC de suivi est également lent à répondre à tous les changements de pas, alors qu'un ADC à pente unique ou à compteur enregistrera un changement de pas de haut en bas plus rapidement qu'un changement de pas de bas en haut.

Les ADC à approximations successives sont presque aussi rapides à résoudre n'importe quel signal analogique, mais un ADC de suivi bat systématiquement un ADC à approximations successives si le signal change plus lentement qu'un pas de résolution par impulsion d'horloge.

J'ai classé les convertisseurs intégrateurs comme ayant un rapport résolution/complexité supérieur à celui des convertisseurs à compteur, mais cela suppose que les circuits intégrateurs analogiques de précision sont moins complexes à concevoir et à fabriquer que les DAC de précision requis dans les convertisseurs à compteur. D'autres peuvent ne pas être d'accord avec cette hypothèse.