Transformation de phase anisotrope dans l'alliage cristallin CuZr B2

Introduction

Les verres métalliques en vrac (BMG) ont attiré une attention considérable en raison de leurs excellentes propriétés mécaniques et physiques, telles qu'une résistance élevée, une élasticité, une dureté élevée combinée à une excellente résistance à la corrosion, etc. [1,2,3,4]. Néanmoins, ils échouent généralement par rupture fragile catastrophique à travers des bandes de cisaillement localisées [5, 6]. Cette lacune a été surmontée dans une certaine mesure dans certains composites de verre métallique en vrac (BMGC) à base de CuZr renforcés par des particules de CuZr en phase B2 ductiles [3, 7,8,9,10,11]. De plus, certaines précipitations de CuZr cristallin B2 seraient formées de manière inhérente par cristallisation dans du verre CuZr sous charge, puis subiraient un macle et un glissement de dislocation, induisant le changement des propriétés mécaniques des BMG, comme cela a été trouvé dans l'expérience [12]. Pour durcir les BMG avec des précipitations CuZr en phase B2 et concevoir des BMG hautes performances, les comportements de déformation de la phase B2 CuZr doivent être clarifiés dans un premier temps.

La phase B2 CuZr est une sorte d'alliage à mémoire de forme qui a la capacité de récupérer sa forme d'origine dans des conditions thermomécaniques spécifiques [13, 14], ce qui est différent des matériaux cristallins traditionnels qui prennent le glissement de dislocation ou le jumelage comme principal mécanisme de déformation [15,16,17]. Le calcul du premier principe basé sur la théorie de la densité fonctionnelle peut être utilisé pour étudier le processus d'adsorption [18,19,20] et la propriété interfaciale [21,22], mais ne peut pas être appliqué pour étudier l'évolution dynamique des comportements de transition de phase en raison à la limitation de l'échelle de calcul. La simulation de dynamique moléculaire (MD) est une méthode efficace pour étudier les propriétés mécaniques et les comportements de déformation des matériaux [23,24,25,26,27,28,29,30,31]. Sutrakar et Mahapatra ont étudié les effets des dimensions de la section transversale et de la température sur la transformation de phase dans les nanofils de Cu-Zr, ainsi que l'asymétrie tension-compression par simulation MD [32,33,34], et ont obtenu des résultats intéressants. Par exemple, la phase B2 initiale est transformée en une phase tétragonale centrée (BCT) par la nucléation et la propagation d'un plan de jumelage {100}. Amigo et al. ont utilisé deux types de potentiels [35, 36] dans leurs simulations MD pour étudier les comportements de transformation de phase, et ont constaté que l'un donne la transformation martensitique de la structure B2 à la structure BCT, tandis que l'autre ne le fait pas [13].

On sait que l'anisotropie des cristaux joue un rôle important dans la déformation des matériaux. Différents mécanismes de déformation peuvent jouer des rôles dominants lors de la déformation lorsque la charge est appliquée le long de différentes orientations cristallines [37]. Par exemple, le glissement parfait de la dislocation et le jumelage sont les principaux mécanismes de déformation pour la nanoindentation sur les surfaces (001) et (111) du nitrure de vanadium (VN) avec un pénétrateur cylindrique [38, 39], respectivement, montrant une plasticité anisotrope évidente. Pour le nanofil de fer BCC, la transformation de phase montre une dépendance complexe de l'orientation cristallographique, le long de laquelle la charge est appliquée, le fil orienté <001> présente une transformation BCC→FCC, mais le fil orienté <011> et <111> suit un BCC→ Transformation HCP [40]. Le réseau de distribution atomique dans la structure B2 est analogue à celui d'une structure BCC, mais il existe deux types d'éléments dans la structure B2. L'orientation cristalline des particules de renforcement dans les BMG est généralement dispersée, ainsi la direction de chargement devrait avoir des influences différentes sur l'effet de durcissement de différentes particules. Ainsi, il est nécessaire d'étudier le comportement de déformation des particules d'amélioration avec un chargement le long de différentes orientations.

Tension et compression uniaxiales, comme deux modes de chargement de base habituellement utilisés pour évaluer les propriétés mécaniques fondamentales des matériaux. Dans ce travail, une série de simulations MD d'essais de traction et de compression uniaxiale de CuZr cristallin B2 le long des orientations [001], [110] et [111] sont menées pour explorer la dépendance de la transformation de phase sur l'orientation de chargement et la tension et la compression (T/C) asymétrie.

Méthodes

La méthode bien connue des atomes intégrés (EAM) [41] est sélectionnée pour décrire la force interatomique du système Cu-Zr. Le potentiel EAM a été largement utilisé pour étudier le comportement mécanique des métaux et de leurs alliages [42,43,44,45,46]. Sur la base du cadre de l'EAM, Mendelev et ses collègues ont identifié et optimisé les paramètres potentiels à trois reprises en 2007 [35], 2009 [36] et 2016 [47]. Dans ce travail, les paramètres de la dernière version du potentiel interatomique pour Cu-Zr [47] développé en 2016 sont utilisés. Ces paramètres peuvent donner une énergie de défaut d'empilement stable et instable plus réaliste par rapport à celle développée en 2009 [36], et peuvent mieux décrire les propriétés du CuZr cristallin.

Trois échantillons avec le chargement axial z le long des [001], [110] et [111] sont préparés, respectivement, comme le montre la figure 1. Avant le chargement, un algorithme de gradient conjugué (CG) est utilisé pour minimiser l'énergie du système pour atteindre une stabilité optimisée. configuration. Des tests mécaniques sont simulés à température ambiante de 300 K. Ensuite, le système est relaxé avec l'ensemble NPT isotherme-isobarique à T =300 K pendant 20 ps pour atteindre un état d'équilibrage sans pression. On constate que l'effet de la vitesse de déformation du matériau nano-polycristallin devient insignifiant car la vitesse de déformation varie dans la plage entre 5 × 10 ⁸ et 1 × 10 ⁹ s ⁻¹ , donc le taux de déformation est attribué à 1 × 10 ⁹ s ⁻¹ en considérant de manière globale à la fois la précision et l'efficacité du calcul [48, 49]. Par conséquent, chaque échantillon est étiré/compressé dans le z -direction à une vitesse de déformation de 10 ⁹ s ⁻¹ pendant le chargement ; pendant ce temps, l'ensemble NPT avec barostat Nose/Hoover est utilisé [50] pour maintenir la pression libre dans x - et y -directions. Dans la phase de relaxation et de chargement, des conditions aux limites périodiques sont appliquées dans x -, y -, et z -directions.

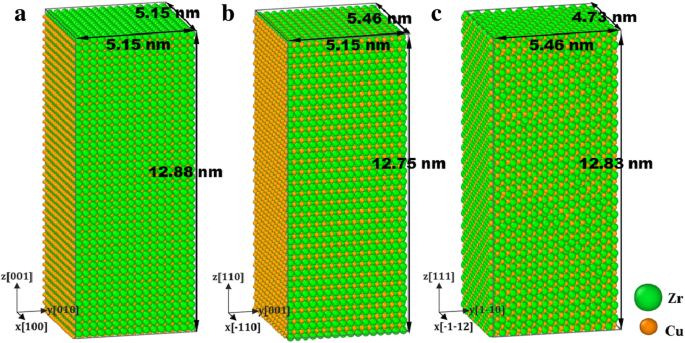
Échantillons avec z axial le long de a [001], b [110], et c [111], coloré avec le type atomique

L'analyse des voisins communs (CNA) [51], un algorithme pour caractériser l'environnement structurel local, est généralement utilisée comme méthode efficace pour classer les atomes dans un système cristallin. La distance du deuxième voisin le plus proche dans une structure BCC n'est que de 15 % plus grande que la plus proche ; par conséquent, la méthode CNA perdrait une certaine fiabilité en présence de fortes fluctuations thermiques et de contraintes. Pour surmonter ce court-circuit, la méthode d'appariement de modèles polyédriques (PTM) a été proposée pour classer l'environnement structurel local des particules et identifier la structure cristalline locale des phases condensées simples (FCC, BCC, HCP, etc.) [52]. Par rapport à la CNA [51], la méthode PTM promet une plus grande fiabilité en présence de fortes fluctuations thermiques et de contraintes [52]. Les structures B2 et BCC ont un arrangement atomique analogue; par conséquent, la structure BCC identifiée par cette méthode est en fait la structure B2. Après l'analyse de la microstructure locale pour les données obtenues par simulation MD avec PTM, les atomes sont colorés selon les règles suivantes :bleu pour structure BCC (B2), vert pour structure FCC, rouge pour empilement de failles ou structure HCP, violet pour cubique simple (SC) et blanc pour les joints de grains ou les noyaux de dislocation. Il convient de noter que les atomes rouges à couche unique, à double couche et multicouches continus sont représentés respectivement par une frontière jumelle, une faille d'empilement et une structure HCP. Les régions locales contenant des atomes rouges, verts, bleus et blancs sont amorphes.

En tant que méthode complémentaire d'analyse de la microstructure, le paramètre de centro-symétrie (CSP) est utilisé pour décrire le désordre local [53]. Pour chaque atome, le CSP est calculé avec la formule fluide :

où N = 12 ou 8 est le nombre des premiers voisins les plus proches d'un atome central dans la structure FCC ou B2, et R _i et R _i+N/2 sont les vecteurs de l'atome central à une paire particulière de voisins les plus proches. Le CSP est nul pour un atome dont les voisins les plus proches sont à leurs sites de réseau parfaits. S'il y a un défaut tel qu'une lacune ou une dislocation à proximité d'un atome, le CSP de l'atome deviendra beaucoup plus grand que celui causé par la vibration atomique locale. Le logiciel ouvert Ovito développé par Stukowski [54] est utilisé pour afficher les configurations atomiques.

Résultats et discussions

Courbes de contrainte-déformation

La figure 2 montre la contrainte-déformation (σ -ε ) courbes pour la phase B2 CuZr soumis à une traction et une compression uniaxiales selon [001], [110] et [111]. On peut noter que la contrainte est plus grande que celle de l'expérience [55], car (1) l'échelle de temps utilisée dans la simulation MD diffère de celle utilisée dans l'expérience, ce qui entraîne une vitesse d'indentation beaucoup plus grande que celle de l'expérience ; et (2) les défauts, y compris les défauts ponctuels, les dislocations et les joints de grains, etc. ne sont pas pris en compte dans les simulations. Au stade initial, ces courbes se développent linéairement et présentent ensuite des tendances différentes. Après le premier pic, ces courbes peuvent être divisées en trois groupes. Dans le groupe I, les courbes chutent rapidement à de faibles niveaux de contraintes, telles que la compression le long de [110] et [111]. Dans le groupe II, les contraintes tombent sur une plate-forme et fluctuent avec l'augmentation de la déformation après le premier pic, telles que la tension le long de [001], [110] et la compression le long de [001]. Les courbes montent ensuite vers leurs deuxièmes sommets avant la chute brutale finale. Dans le groupe III, la courbe chute rapidement à de faibles niveaux de contrainte, puis fluctue en zigzag, comme la tension le long de [111]. Avant le premier pic, les échantillons restent dans la structure B2 et aucun glissement de dislocation et aucun jumelage évidents ne peuvent être observés, ce qui peut être considéré comme la déformation élastique. Au stade élastique linéaire, le module de Young E peut être obtenu en ajustant la pente de chaque courbe dans la plage de 0,00 <ε <0,02, et répertorié dans le tableau 1, où l'on peut voir que l'orientation [001] est la plus douce et [111] est la plus rigide. Ceci est en accord avec les résultats du fer BCC en vrac [40]. Le E de l'échantillon sous compression est plus grande que celle sous tension à l'exception de l'orientation [001], en cohérence avec celle observée dans le monocristal de Cu [56], qui doit être attribuée au frottement plus élevé sous compression [56]. Le reste des courbes au stade élastique sous compression s'écartent évidemment de celle sous tension, ce qui doit être attribué à la nature asymétrique en traction et en compression du potentiel interatomique [57]. Après le premier pic, il n'est pas clair si la déformation doit être attribuée au glissement de la dislocation ou à la transformation de phase ; par conséquent, cette région ne peut pas être considérée comme une asymétrie T/C inélastique ou plastique, ce qui diffère des travaux des autres [57,58,59]. Dans la section coulante, les mécanismes de déformation de l'échantillon soumis à des chargements dans différentes directions seront discutés en détail.

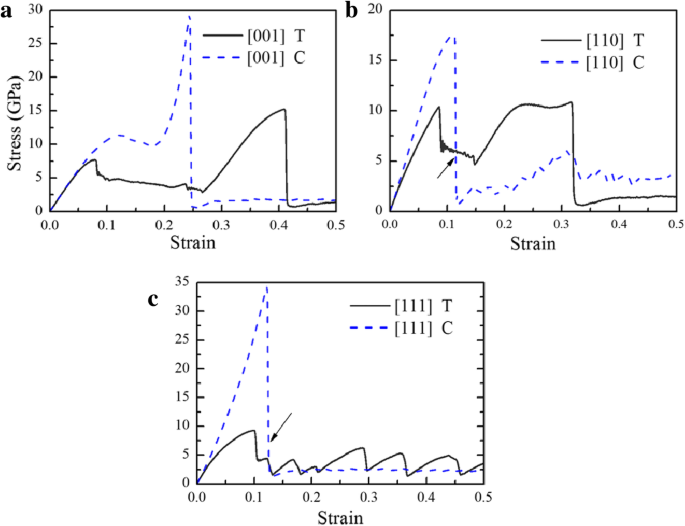
σ -ε courbes d'échantillons en traction (T) et en compression (C). un [001], b [110] et c [111]

Comportement d'échec

La figure 3 montre les structures atomiques et les fonctions de distribution radiale (RDF) des échantillons soumis à compression selon [110] et [111], dont σ -ε les courbes peuvent être vues dans la Fig. 2 étiquetées comme [110] C et [111] C. La figure 3a, d montre les échantillons initiaux [110] et [111] après relaxation à 300 K, où on peut voir que les atomes sont dans la structure B2. Quand ε est augmenté à 0,115 ou 0,125 pour [110] C et [111] C, respectivement, la région avec des structures mixtes apparaît, comme le montre la Fig. 3b, f. La structure dans la zone mixte est définie comme une phase mixte. La nucléation de la phase mixte correspond au stade de gouttes rapides des courbes [110] C et [111] C de la figure 2b, c, qui est marqué par des flèches. Par conséquent, la transformation de la structure locale de B2 en une phase mixte provoque la chute rapide des contraintes. Au stade de l'écoulement, la variation de la fraction volumique de la phase mixte est le mécanisme principal pour s'adapter à une déformation supplémentaire, les structures locales dans les échantillons sous compression le long de [110] et [111] à ε =0,25 sont indiqués sur la figure 3c, g, respectivement. Pour spécifier la structure dans la région mixte, la fonction de distribution radiale (RDFs ), g (r ), des échantillons en compression le long de [110] et [111] à différentes déformations sont représentés sur la Fig. 3d, h. Les sommets du g (r ) des échantillons à ε =0 et ε =0,25 sont nets, indiquant qu'ils conservent toujours une caractéristique cristalline. Alors que les sommets du g (r ) pour les régions mixtes, c'est-à-dire l'échantillon sans régions B2, sont émoussés sauf les premiers, indiquant que la région mixte est dans un état amorphe. L'algorithme d'extraction de dislocation (DXA) [60] est également utilisé pour détecter s'il y a une nucléation de dislocation et ne trouver aucune dislocation évidente tout au long du processus de déformation. Par conséquent, l'amorphisation de la phase B2 est menée pour être le mode de défaillance principal, entraînant la chute rapide, marquée par des flèches sur les Fig. 2b, c.

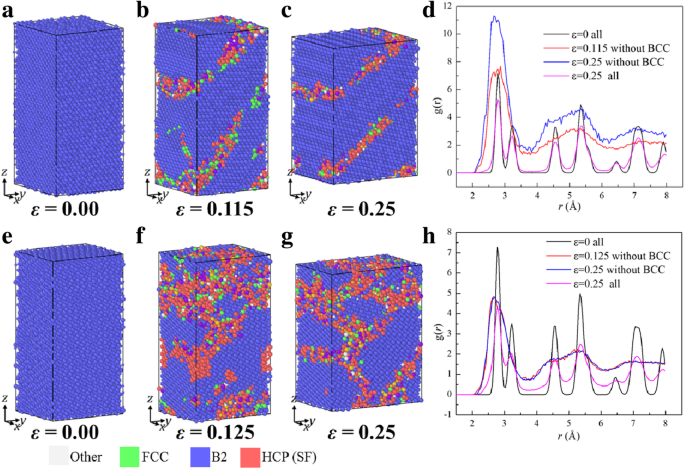
Configurations atomiques et RDF d'échantillons sous compression. un –d Le long de [110] et e –h le long de [111]

La figure 4 montre les configurations atomiques après la déformation de chute rapide (déformation de rupture) des échantillons en traction selon [001], [110] et compression selon [001], dont σ -ε les courbes appartiennent au groupe II. On peut voir sur la figure 4 que des régions mixtes se forment, similaires à celles du groupe I, indiquant que l'amorphisation est également le principal mode de défaillance (figure 4). Cependant, ces régions mixtes sont entourées d'atomes verts et rouges (structure FCC et HCP), ce qui est différent de la structure B2 de la figure 3. Cette différence indique que la phase mixte est transformée à partir de la structure B2 sous compression de la figure 3, mais de FCC pour l'échantillon [001] en traction et compression, et de HCP pour l'échantillon [110] en traction.

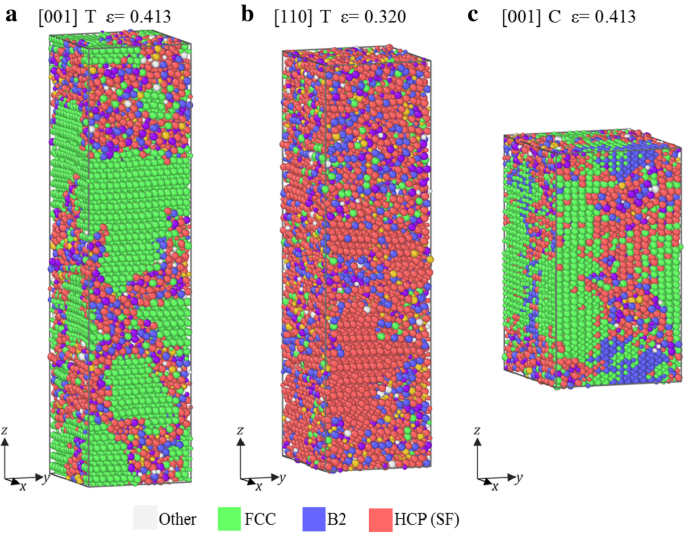
Configurations atomiques dans des échantillons à déformation de rupture. un Sous tension le long de [001], b sous tension le long de [110], et c sous compression le long de [111]

Transformations de phase

La figure 5 montre le σ -ε courbe de l'échantillon [001] sous tension, où les microstructures à des points typiques (marqués par A, B, ..., G) sont également présentées. Les atomes au point A (ε =0,079) sont dans la structure B2, indiquant qu'avant ε =0,079 la déformation dans l'échantillon est élastique. Cependant, une transformation locale de B2 en FCC a lieu, comme indiqué dans l'encart de ε =0,082 sur la figure 5, résultant en la première chute rapide (A→B) à ε =0,082, où la libération de l'énergie élastique stockée en raison de la redistribution de la configuration atomique fournit l'énergie nécessaire à la transformation de phase. Dans l'étape d'écoulement de B→F, l'énergie élastique stockée est davantage libérée au fur et à mesure que la transformation de phase se poursuit, conduisant à la réduction de la contrainte. La structure locale de l'échantillon devient FCC complètement à ε =0,242 (point E). Et la structure continue de changer entre les points E et F, mais la contrainte continue de baisser avec l'augmentation de la déformation. Pour révéler le changement de microstructure, la distribution de g (r ) et la variation du nombre d'atomes (N ) contre CSP (N -CSP ) de l'échantillon à ε =0,242, 0,254 et 0,267 (entre les points E et F) sont calculés et représentés sur les figures 6a, b, respectivement, où la hauteur de chaque pic augmente avec l'augmentation de la contrainte, indiquant que le système devient plus compact.

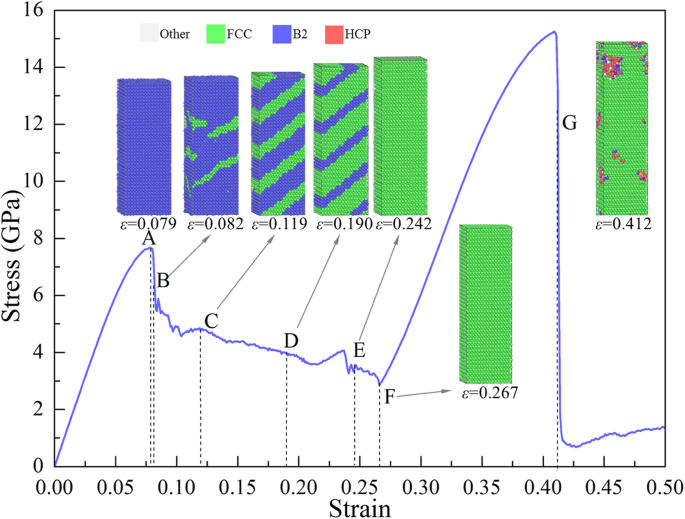
σ-ε courbe de l'échantillon sous tension le long de [001], colorée avec la structure locale, avec respectivement bleu, vert et rouge représentant les phases B2, FCC et amorphe

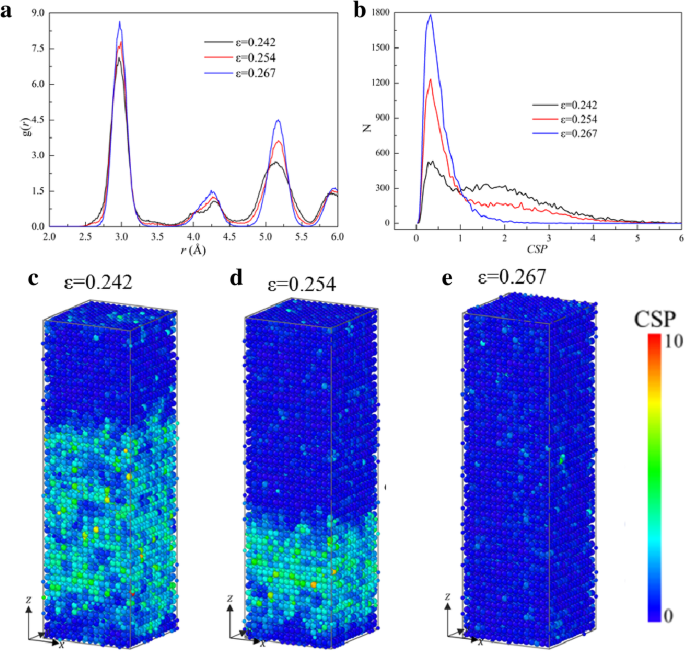
un RDF , b N -CSP tracés d'échantillon sous tension le long de [001]. c –e Distribution de CSP dans l'échantillon à différentes souches

Pour caractériser si un atome fait partie d'un réseau parfait ou d'un défaut local, par exemple, une faille de dislocation ou d'empilement, ou une surface, le CSP [53] des atomes avec le nombre de plus proches voisins de la structure FCC (N =12) sont calculés, comme le montre la Fig. 6c–e. Et un CSP plus grand signifie un écart plus important par rapport au réseau parfait [17]. On peut voir sur la figure 6b que le nombre d'atomes avec CSP < 1 augmente avec l'augmentation de la déformation, ce qui peut également être vu plus intuitivement à partir de la distribution des CSP des atomes sur la figure 6c–e. Cela diffère des résultats courants selon lesquels le CSP ne diminuerait généralement pas avec l'augmentation de la contrainte. Par conséquent, les principaux comportements de déformation dans cette étape devraient également être attribués à la transformation de phase du FCC imparfait au FCC parfait. Dans la phase d'écoulement, l'échantillon avec des structures FCC est étiré et la contrainte augmentera jusqu'à atteindre le deuxième seuil d'élasticité. Puis la courbe chute fortement, correspondant à une amorphisation locale plutôt qu'à la nucléation de la luxation ou du glissement.

Pour illustrer la transformation de phase du matériau lors de la déformation, la figure 7 montre quelques yoz tranches de l'échantillon [001] sous tension à différentes déformations. Les lignes pointillées horizontales et verticales sont utilisées comme références pour identifier si les structures atomiques tournent et s'écartent. Avec l'augmentation de ε de 0,0 à 0,079, les atomes se trouvent sur des lignes parallèles aux axes horizontal et vertical, indiquant qu'ils sont de structure locale B2. Cependant, le réseau atomique de la figure 7b devient celui de la figure 7c en tant que ε de 0,079 à 0,119 lorsque certaines structures B2 se transforment en structure FCC. L'angle entre les réseaux passe de 90° sur la figure 7b pour la structure B2 à ~ 85° sur la figure 7c pour la structure FCC avec l'orientation du réseau s'écartant de l'axe vertical de 5° dans le sens des aiguilles d'une montre, mais le réseau atomique de la structure B2 ne changer évidemment et n'a pas de rotation évidente. Pendant 0,119 <ε < 0,190, la zone FCC augmente et le réseau d'atomes verts tourne progressivement dans le sens inverse des aiguilles d'une montre. À ε =0,242, toute la structure B2 se transforme en structures FCC, comme le montre la figure 7e, où les trois orientations du réseau deviennent presque parallèles aux trois axes respectivement, mais il y a toujours un écart marqué, indiquant que la structure FCC n'est pas parfaite, ce qui est en cohérence avec celui représenté sur la figure 6c. Dans la phase d'écoulement, le réseau atomique tend régulièrement, comme le montre la figure 7f à ε =0,267, qui est reconnu comme un plan {110} de structure FCC, avec son orientation cristalline dans les directions horizontale et verticale modifiée de [010] et [001] de structure B2 à <110> et <001> de structure FCC.

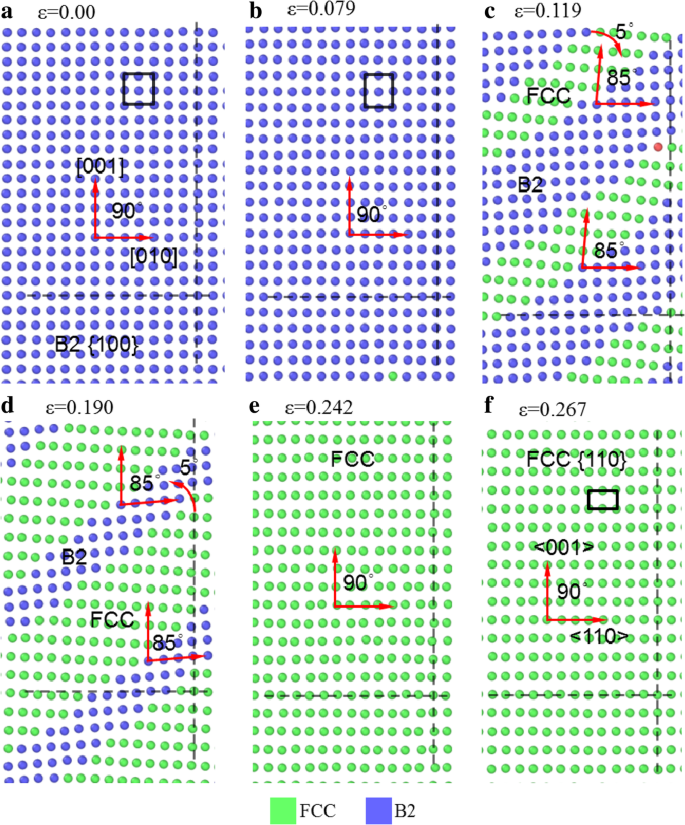
yoz tranches d'échantillon [001] sous tension à différentes déformations, colorées avec une structure en réseau local, avec des phases bleue, verte et rouge représentant respectivement B2, FCC et amorphe

La simulation de la réponse de l'échantillon (100) lors du déchargement à partir de différentes contraintes de traction maximales (ε _max =0,1, 0,2 et 0,3, respectivement) sont effectuées, et le σ -ε les courbes sont représentées sur la Fig. 8. On peut voir que le déchargement σ -ε courbes entre ε =0,266 et ε =0,056 ne chevauchent pas la courbe de chargement, mais ils peuvent rencontrer l'élastique σ -ε courbe à ε =0,056 puis retour à l'origine le long de l'élastique σ -ε courbe, présentant la caractéristique superélastique. Les chemins de chargement et de déchargement forment des boucles d'hystérésis, qui doivent être attribuées aux différents chemins d'acheminement et de transformations de phase inverse.

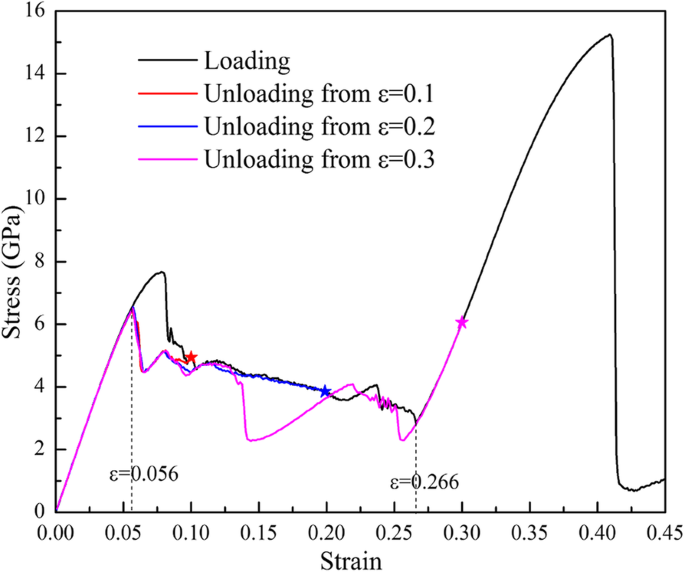
Chargement et déchargement σ -ε courbe la tension le long de [001] à partir de différentes déformations

Le σ -ε courbe de l'échantillon [001] sous compression a une tendance similaire, comme le montre la figure 9a, qui peut être divisé en quatre étapes :(1) σ augmente linéairement avec l'augmentation de la déformation ; (2) σ tombe à un plateau; (3) σ augmente linéairement avec une pente plus grande jusqu'au deuxième pic en tant qu'augmentation de la déformation ; (4) σ chute brutalement jusqu'au deuxième plateau. En analysant les structures locales avec PTM, on peut constater que la plupart des atomes sont identifiés comme structure B2 avant d'atteindre le deuxième pic, à l'exception de certains atomes dispersés qui sont identifiés comme une autre structure locale, comme le montre la figure 9a. Cependant, selon la compréhension précédente, un changement soudain dans le σ -ε courbes correspond généralement au changement de microstructure. Pour le confirmer davantage, le N -CSP les parcelles sont calculées et présentées sur la figure 9b, dans laquelle le CSP pour chaque atome à différentes contraintes est calculé avec les voisins les plus proches de la structure B2 (N =8). Quand ε =0, le CSP d'atomes est supérieur à 0, mais inférieur à 1, en raison de l'effet de la température, ce qui implique que les atomes sont dans une structure B2 parfaite. Avec l'augmentation de ε , les atomes peuvent être divisés en deux groupes par leurs CSP :CSP < 1 et 5 ε < 0,121, les CSP aux deuxièmes pics sont les mêmes, mais le nombre d'atomes dans ce CSP la plage augmente et tend à se stabiliser, indiquant la formation de nouvelles phases ou de nouveaux défauts (tels qu'un défaut d'empilement). Le CSP au deuxième pic diminue avec l'augmentation supplémentaire de ε , c'est-à-dire que la deuxième vague se déplace vers la gauche. La figure 10 montre l'évolution de la longueur de liaison dans une maille unitaire à différentes contraintes. À ε =0, huit atomes de Cu aux sommets et un atome de Zr au centre du corps constituent la structure B2. La relation entre les paramètres du réseau est a =b =c . Avec l'augmentation de ε , la longueur de la liaison en xoy l'avion augmente, mais celui en xoz avion diminue. En calculant la déformation dans les deux autres directions lors du chargement, on peut constater que les déformations dans les deux autres directions sont identiques avant les deuxièmes pics. Par conséquent, les longueurs des liaisons le long de x- et y -les directions doivent être identiques et plus grandes que celles le long du z -direction. La relation entre les paramètres du réseau devient a =b> c . Ces réseaux d'atomes peuvent être reconnus comme une structure BCT. En conclusion, la transformation d'une structure B2 en structure BCT est le principal mécanisme de déformation de l'échantillon [001] sous compression.

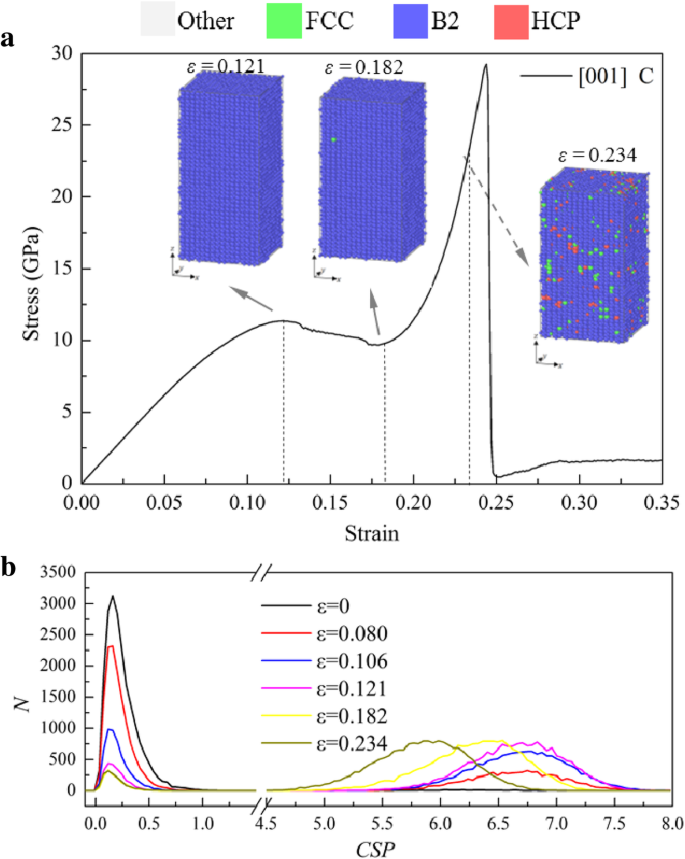
Réponses de l'échantillon [001] sous compression. un σ-ε courbe et configurations atomiques typiques, avec des atomes colorés avec des structures locales identifiées par PTM. b N -CSP parcelles

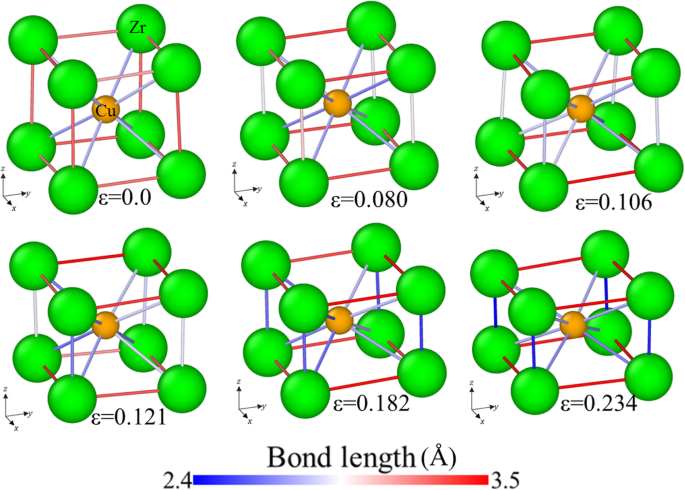
Evolution de la longueur de liaison pour l'échantillon [001] en compression, avec des liaisons colorées avec sa longueur

La figure 11a montre la réponse de l'échantillon [110] sous tension. Le premier pic (point A) correspond à la limite d'élasticité de la structure B2, puis une certaine structure B2 locale se transforme en structure HCP, entraînant la chute brutale. Avec l'augmentation de ε , la contrainte diminue jusqu'au point C où l'échantillon se transforme totalement en HCP. Figure 11b, c est le xoy tranches à une couche à ε =0 et 0,150, respectivement, où l'on peut voir qu'au stade initial les atomes Cu et Zr sont dans une couche atomique identique (Fig. 11b). Cependant, les atomes de Cu et de Zr sont séparés en couches adjacentes à ε =0,150 (Fig. 11c), ce qui entraîne la transformation de phase de B2 en HCP. Puis avec l'augmentation de ε , σ augmente avec une pente plus faible que celle de la phase linéaire initiale jusqu'au point D, suivie d'une chute brutale jusqu'à un niveau de contrainte faible, correspondant à une rupture due à une amorphisation locale.

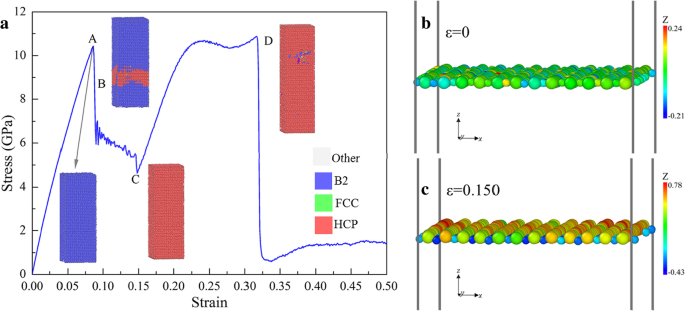
un Comportement en déformation de traction selon [110], coloré au PTM. b , c Tranches atomiques sur xoy plan à ε =0 et 0,150, respectivement

Conclusions

Dans ce travail, les réponses et la transformation de phase d'échantillons de CuZr soumis à des tractions et compressions uniaxiales selon les orientations [001], [110], [111] sont étudiées respectivement à l'aide de simulations de dynamique moléculaire, en utilisant le dernier potentiel interatomique, à partir duquel le Les principales conclusions suivantes peuvent être tirées :

1. 1.

   Les réponses mécaniques des échantillons de CuZr en traction et en compression présentent une asymétrie évidente, et leur principal mécanisme de rupture devrait être l'amorphisation locale.

2. 2.

   Il existe trois types de transformations de phase :B2→FCC, B2→BCT et B2→HCP en traction et compression le long de [001], et en tension le long de [110].

3. 3.

   Les transformations de phase B2→FCC, B2→BCT et B2→HCP sont réalisées respectivement par des mécanismes uniques qui sont la rotation du réseau (~ 5°), la déformation uniforme et la séparation de la couche atomique de Cu et Zr pour chacune.

4. 4.

   La région de transformation de phase peut être récupérée après déchargement avant amorphisation locale, montrant la superélasticité.

Les résultats sont importants pour l'exploration des propriétés mécaniques et des mécanismes de déformation du CuZr nanocristallin, et pour les applications des particules de CuZr nanocristallin en tant qu'agent d'amélioration pour améliorer la ténacité du verre métallique.

Disponibilité des données et des matériaux

Les ensembles de données utilisés ou analysés au cours de la présente étude sont disponibles auprès de l'auteur correspondant sur demande raisonnable.

Abréviations

Cci :

Cube centré sur le corps

BCT :

Corps-centrée-tétragonale

BMG :

Verres métalliques en vrac

BMGC :

Composites de verre métallique en vrac

CG :

Dégradé conjugué

AIIC :

Analyse des voisins communs

CSP :

Paramètre de centro-symétrie

Cu :

Cuivre

CuZr :

Cuivre-zirconium

DXA :

Algorithme d'extraction de luxation

MAE :

Méthode de l'atome embarqué

FCC :

Cube à faces centrées

HCP :

Hexagonal compact

MD :

Dynamique moléculaire

NPT :

Nombre constant de particules, pression et température

PTM :

Correspondance de modèle polyédrique

RDF :

Fonction de distribution radiale

Conditions générales :

Tension et compression

VN :

Nitrure de vanadium

Zr :

Zirconium

ε :

Souche

σ :

Stress