Harmoniques dans les systèmes d'alimentation polyphasés
Dans le chapitre sur les signaux à fréquences mixtes, nous avons exploré le concept des harmoniques dans les systèmes AC :fréquences qui sont des multiples entiers de la fréquence fondamentale de la source.
Avec les systèmes d'alimentation CA où la forme d'onde de tension source provenant d'un générateur CA (alternateur) est censée être une onde sinusoïdale à fréquence unique, non déformée, il ne devrait y avoir aucun contenu harmonique. . . idéalement.
Composants non linéaires sur les systèmes AC
Ce serait vrai sans les composants non linéaires . Les composants non linéaires consomment du courant de manière disproportionnée par rapport à la tension source, provoquant des formes d'onde de courant non sinusoïdales.
Des exemples de composants non linéaires comprennent les lampes à décharge de gaz, les dispositifs de commande de puissance à semi-conducteurs (diodes, transistors, SCR, TRIAC), les transformateurs (le courant de magnétisation de l'enroulement primaire est généralement non sinusoïdal en raison de la courbe de saturation B/H du noyau), et moteurs électriques (encore une fois, lorsque les champs magnétiques dans le noyau du moteur fonctionnent près des niveaux de saturation).
Même les lampes à incandescence génèrent des courants légèrement non sinusoïdaux, car la résistance du filament change tout au long du cycle en raison des fluctuations rapides de température.
Comme nous l'avons appris dans le chapitre sur les fréquences mixtes, tout la distorsion d'une forme d'onde autrement sinusoïdale constitue la présence de fréquences harmoniques.
Lorsque la forme d'onde non sinusoïdale en question est symétrique au-dessus et au-dessous de sa ligne médiane moyenne, les fréquences harmoniques seront des multiples entiers impairs de la fréquence source fondamentale uniquement, sans multiples entiers pairs.
La plupart des charges non linéaires produisent des formes d'onde de courant comme celle-ci, et donc les harmoniques paires (2e, 4e, 6e, 8e, 10e, 12e, etc.) sont absentes ou peu présentes dans la plupart des systèmes d'alimentation CA.
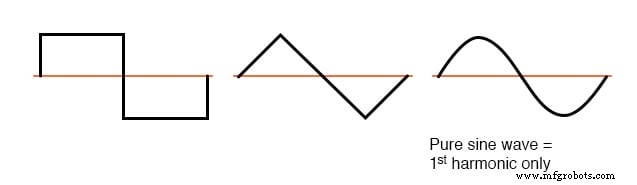
Exemples de formes d'onde symétriques — harmoniques impaires uniquement.
Des exemples de formes d'onde non symétriques avec des harmoniques paires présentes sont indiqués à titre de référence dans la figure ci-dessous.
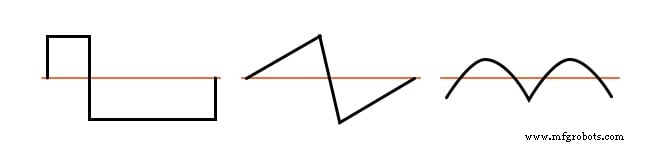
Exemples de formes d'onde non symétriques, même harmoniques présentes.
Même si la moitié des fréquences harmoniques possibles sont éliminées par la distorsion typiquement symétrique des charges non linéaires, les harmoniques impaires peuvent toujours causer des problèmes. Certains de ces problèmes sont généraux à tous les systèmes d'alimentation, monophasés ou non.
La surchauffe du transformateur due aux pertes par courants de Foucault, par exemple, peut se produire dans n'importe quel Système d'alimentation CA où il y a un contenu harmonique important.
Cependant, il existe certains problèmes causés par les courants harmoniques qui sont spécifiques aux systèmes d'alimentation polyphasés, et ce sont ces problèmes auxquels cette section est spécifiquement consacrée.
Simulation SPICE concernant les effets harmoniques
Il est utile de pouvoir simuler des charges non linéaires dans SPICE afin d'éviter beaucoup de mathématiques complexes et d'obtenir une compréhension plus intuitive des effets harmoniques.
Simulation de système CA linéaire
Tout d'abord, nous allons commencer notre simulation avec un circuit alternatif très simple :une seule source de tension sinusoïdale avec une charge purement linéaire et toutes les résistances associées :
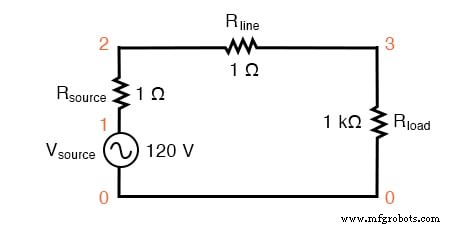
Circuit SPICE avec une seule source d'onde sinusoïdale.
La Rsource et Rligne les résistances de ce circuit font plus que simplement imiter le monde réel :elles fournissent également des résistances shunt pratiques pour mesurer les courants dans la simulation SPICE :en lisant la tension aux bornes d'une résistance de 1 , vous obtenez une indication directe du courant qui la traverse, puisque E =IR .
Une simulation SPICE de ce circuit (liste SPICE :« simulation de charge linéaire ») avec analyse de Fourier sur la tension mesurée aux bornes de la ligne R devrait nous montrer le contenu harmonique du courant de ligne de ce circuit. Étant de nature complètement linéaire, nous ne devrions nous attendre à aucune harmonique autre que la 1ère (fondamentale) de 60 Hz, en supposant une source de 60 Hz.
Voir la sortie SPICE « Composantes de Fourier de la réponse transitoire v(2,3) » et la figure ci-dessous.
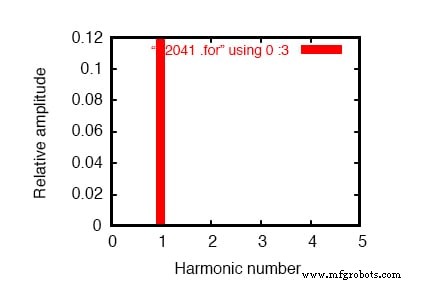
Tracé du domaine de fréquence d'une composante de fréquence unique. Voir la liste SPICE :« simulation de charge linéaire ».
Une commande .plot apparaît dans la netlist SPICE et, normalement, cela se traduirait par une sortie de graphique à onde sinusoïdale. Dans ce cas, cependant, j'ai volontairement omis l'affichage de la forme d'onde par souci de concision :la commande .plot est dans la netlist simplement pour satisfaire une bizarrerie de la fonction de transformation de Fourier de SPICE.
Aucune transformée de Fourier discrète n'est parfaite, et nous voyons donc de très petits courants harmoniques indiqués (dans la plage des pico-amplis !) .
Nous montrons 0,1198 ampères (1,198E-01) pour la « composante de Fourier » du 1er harmonique, ou la fréquence fondamentale, qui est notre courant de charge attendu :environ 120 mA, étant donné une tension de source de 120 volts et une résistance de charge de 1 kΩ.
Simulation de système CA monophasé non linéaire simple
Ensuite, j'aimerais simuler une charge non linéaire afin de générer des courants harmoniques. Cela peut se faire de deux manières fondamentalement différentes. Une façon consiste à concevoir une charge à l'aide de composants non linéaires tels que des diodes ou d'autres dispositifs à semi-conducteurs qui sont faciles à simuler avec SPICE. Une autre consiste à ajouter des sources de courant alternatif en parallèle avec la résistance de charge.
Cette dernière méthode est souvent préférée par les ingénieurs pour simuler les harmoniques, car les sources de courant de valeur connue se prêtent mieux à l'analyse mathématique du réseau que les composants avec des caractéristiques de réponse très complexes.
Puisque nous laissons SPICE faire tout le travail mathématique, la complexité d'un composant semi-conducteur ne nous causerait aucun problème, mais puisque les sources de courant peuvent être affinées pour produire n'importe quelle quantité arbitraire de courant (une fonctionnalité pratique), je vais choisissez cette dernière approche illustrée dans la figure ci-dessous et dans la liste SPICE « Simulation de charge non linéaire ».
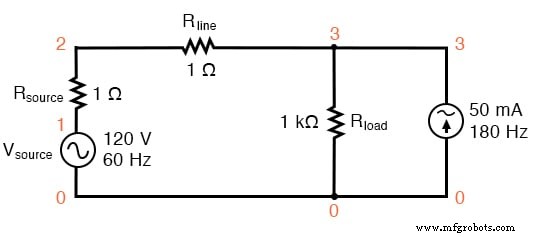
Circuit SPICE :source 60 Hz avec 3e harmonique ajoutée.
Dans ce circuit, nous avons une source de courant d'une amplitude de 50 mA et une fréquence de 180 Hz, soit trois fois la fréquence de la source de 60 Hz. Connecté en parallèle avec la résistance de charge de 1 kΩ, son courant s'ajoutera à celui de la résistance pour former un courant de ligne total non sinusoïdal.
Je vais montrer le tracé de la forme d'onde dans la figure ci-dessous juste pour que vous puissiez voir les effets de ce courant de 3e harmonique sur le courant total, qui serait normalement une onde sinusoïdale simple.
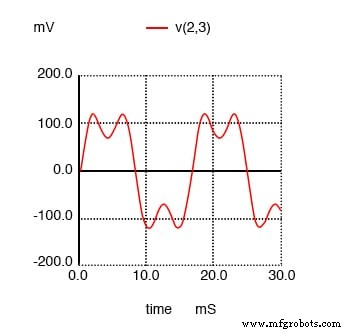
Tracé SPICE dans le domaine temporel montrant la somme de la source de 60 Hz et de la 3e harmonique de 180 Hz.
Composantes de Fourier de la réponse transitoire v(2,3) composante continue =1,349E-11 fréquence harmonique Fourier normalisée phase normalisée non (Hz) composante composante (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.609E-11 0.000000 67.570 139.570 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E+02 3.871E-11 0.000000 169.582 241.582 6 3,600E+02 5,736E-11 0,000000 140,845 212,845 7 4.200E+02 8.407E-11 0,000000 177,071 249,071 8 4.800E+02 1.329E-10 0.000000 156.772 228.772 9 5,400E+02 2,619E-10 0,000000 160,498 232,498 distorsion harmonique totale =41,666663%
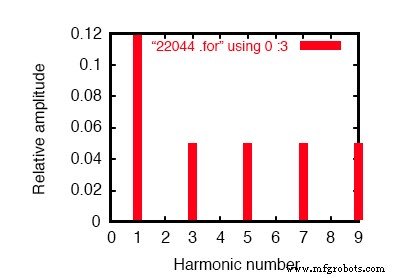
Tracé de Fourier SPICE montrant une source de 60 Hz et une 3e harmonique de 180 Hz.
Dans l'analyse de Fourier (voir la figure ci-dessus et "Composantes de Fourier de la réponse transitoire v(2,3)"), les fréquences mélangées ne sont pas mélangées et présentées séparément.
Ici, nous voyons le même courant de 0,1198 ampères de 60 Hz (fondamental) que dans la première simulation, mais apparaissant dans la 3e rangée harmonique, nous voyons 49,9 mA :notre source de courant 50 mA, 180 Hz au travail. Pourquoi ne voyons-nous pas la totalité des 50 mA à travers la ligne ?
Parce que cette source de courant est connectée à travers la résistance de charge de 1 kΩ, une partie de ses courants est donc shuntée à travers la charge et ne revient jamais par la ligne vers la source. C'est une conséquence inévitable de ce type de simulation, où une partie de la charge est "normale" (une résistance) et l'autre partie est imitée par une source de courant.
Simulation de système CA monophasé non linéaire avec plusieurs sources de courant
Si nous devions ajouter plus de sources de courant à la « charge », nous verrions une distorsion supplémentaire de la forme d'onde du courant de ligne par rapport à la forme d'onde sinusoïdale idéale, et chacun de ces courants harmoniques apparaîtrait dans la décomposition de l'analyse de Fourier. Voir la figure ci-dessous et la liste SPICE :« Simulation de charge non linéaire ».
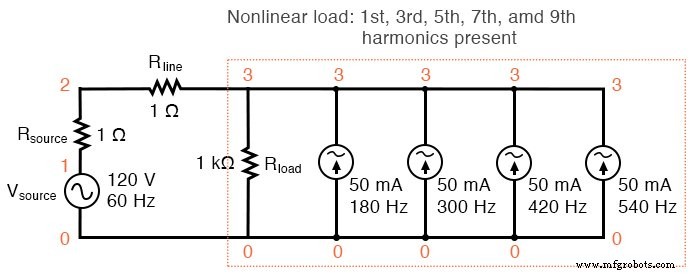
Charge non linéaire :1er, 3e, 5e, 7e et 9e harmoniques présents.
Simulation de charge non linéaire vsource 1 0 sin(0 120 60 0 0) ressource 1 2 1 ligne 2 3 1 charger 3 0 1k i3har 3 0 péché(0 50m 180 0 0) i5har 3 0 péché(0 50m 300 0 0) i7har 3 0 péché(0 50m 420 0 0) i9har 3 0 péché(0 50m 540 0 0) .options itl5=0 .tran 0.5m 30m 0 1u .plot tran v(2,3) .quatre 60 v(2,3) .fin
Composantes de Fourier de la réponse transitoire v(2,3) composante continue =6.299E-11 fréquence harmonique Fourier normalisée phase normalisée non (Hz) composante composante (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 -72.000 0.000 2 1.200E+02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E+02 4.990E-02 0.416667 144.000 216.000 4 2.400E+02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E+02 4.990E-02 0.416667 0.000 72.000 6 3.600E+02 6.271E-09 0.000000 85.062 157.062 7 4.200E+02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E+02 2.742E-09 0.000000 -38.781 33.219 9 5.400E+02 4.990E-02 0.416666 72.000 144.000 distorsion harmonique totale =83,333296 pour cent

Analyse de Fourier :« Composantes de Fourier de la réponse transitoire v(2,3) ».
Comme vous pouvez le voir à partir de l'analyse de Fourier (Figure ci-dessus), chaque source de courant harmonique est également représentée dans le courant de ligne, à 49,9 mA chacune. Jusqu'à présent, il ne s'agit que d'une simulation de système d'alimentation monophasé.
Simulation de système CA triphasé
Les choses deviennent plus intéressantes lorsque nous en faisons une simulation triphasée. Deux analyses de Fourier seront effectuées :une pour la tension aux bornes d'une résistance de ligne et une pour la tension aux bornes de la résistance neutre.
Comme précédemment, la lecture des tensions aux bornes des résistances fixes de 1 chacune donne des indications directes du courant à travers ces résistances. Voir la figure ci-dessous et la liste SPICE « Système Y-Y source/charge à 4 fils avec harmoniques ».
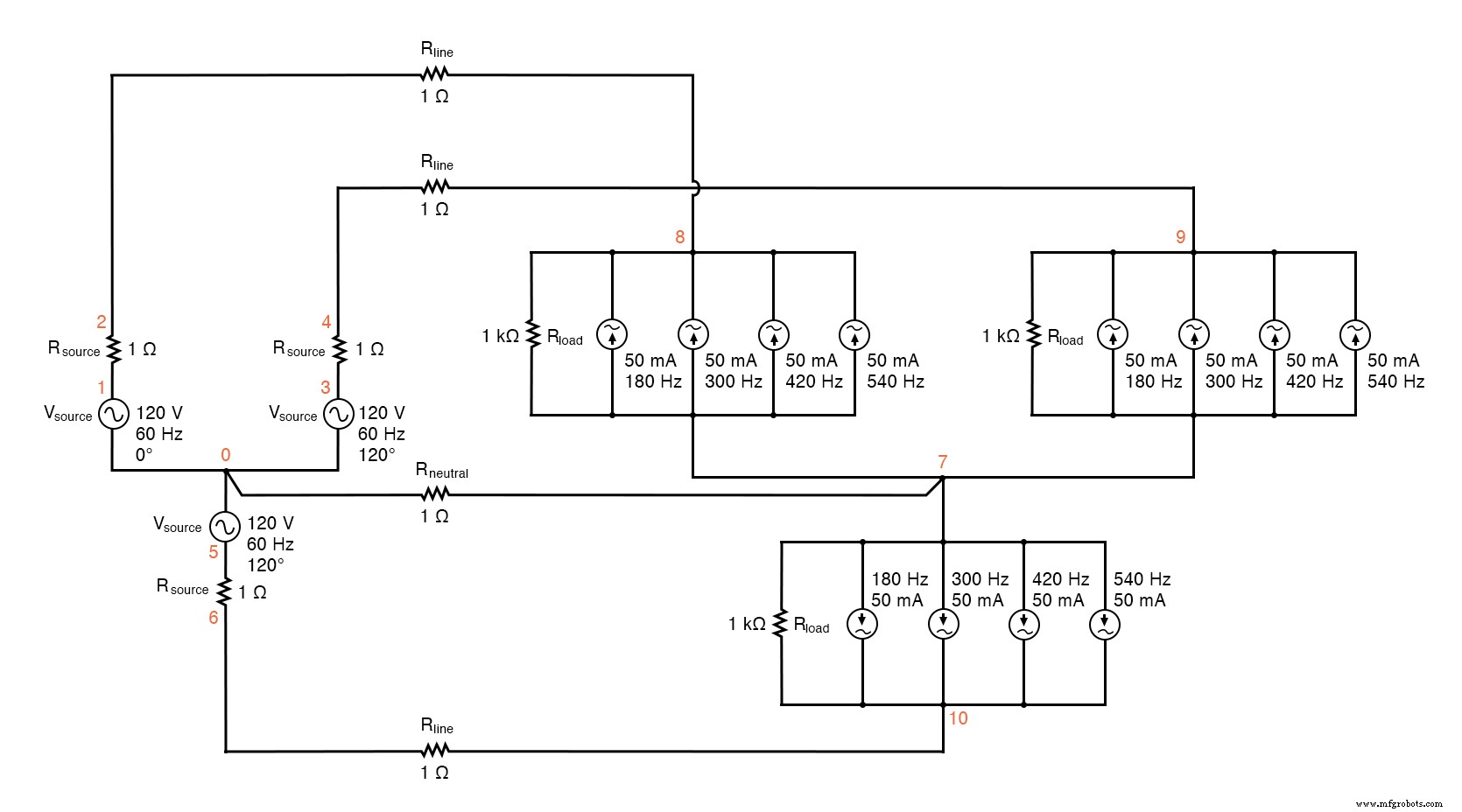
Circuit SPICE :analyse du « courant de ligne » et du « courant de neutre », système Y-Y source/charge à 4 fils avec harmoniques.
Analyse de Fourier du courant de ligne :
Composantes de Fourier de la réponse transitoire v(2,8) composante continue =-6,404E-12 fréquence harmonique Fourier normalisée phase normalisée non (Hz) composante composante (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.218E-10 0.000000 172.985 172.985 3 1.800E+02 4.975E-02 0.415423 0.000 0.000 4 2.400E+02 4.236E-10 0.000000 166.990 166.990 5 3.000E+02 4.990E-02 0.416667 0.000 0.000 6 3.600E+02 1.877E-10 0.000000 -147.146 -147.146 7 4,200E+02 4,990E-02 0,416666 0,000 0,000 8 4.800E+02 2.784E-10 0.000000 -148.811 -148.811 9 5,400E+02 4,975E-02 0,415422 0,000 0,000 distorsion harmonique totale =83,209009 pour cent
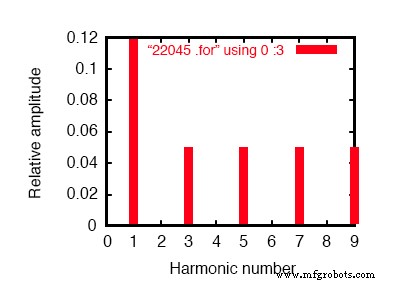
Analyse de Fourier du courant de ligne dans un système Y-Y équilibré.
Analyse de Fourier du courant neutre :
Composantes de Fourier de la réponse transitoire v(0,7) composante continue =1,819E-10 fréquence harmonique Fourier normalisée phase normalisée non (Hz) composante composante (deg) phase (deg) 1 6.000E+01 4.337E-07 1.000000 60.018 0.000 2 1,200E+02 1,869E-10 0,000431 91,206 31,188 3 1.800E+02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E+02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E+02 9.023E-07 2.080596 119.981 59.963 6 3,600E+02 3,396E-10 0,000783 15,882 -44,136 7 4.200E+02 1.264E-06 2.913955 59.993 -0.025 8 4.800E+02 5.975E-10 0.001378 35.584 -24.434 9 5.400E+02 1.493E-01 344147.4889 -179.999 -240.017
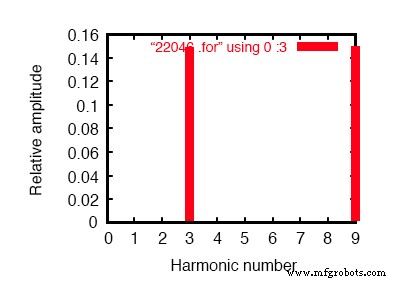
L'analyse de Fourier du courant neutre montre autre chose qu'aucune harmonique ! Comparer au courant de ligne dans la figure ci-dessus.
Il s'agit d'un système d'alimentation Y-Y équilibré, chaque phase étant identique au système CA monophasé simulé précédemment. Par conséquent, il n'est pas surprenant que l'analyse de Fourier pour le courant de ligne dans une phase du système triphasé soit presque identique à l'analyse de Fourier pour le courant de ligne dans le système monophasé :un courant de ligne fondamental (60 Hz) de 0,1198 ampères et courants harmoniques impairs d'environ 50 mA chacun.
Voir la figure ci-dessus et l'analyse de Fourier :« Composantes de Fourier de la réponse transitoire v(2,8) »
Ce qui devrait être surprenant ici, c'est l'analyse du courant du conducteur neutre, tel que déterminé par la chute de tension aux bornes du Rneutre résistance entre les nœuds SPICE 0 et 7.
Dans une charge Y triphasée équilibrée, nous nous attendrions à ce que le courant neutre soit nul. Chaque courant de phase - qui par lui-même traverserait le fil neutre pour revenir à la phase d'alimentation sur la source Y - devrait s'annuler par rapport au conducteur neutre car ils sont tous de la même amplitude et tous décalés de 120 °.
Dans un système sans courants harmoniques, ceci est ce qui se passe, en laissant zéro courant à travers le conducteur neutre.
Effets des courants harmoniques dans le système
Cependant, nous ne pouvons pas en dire autant pour harmonique courants dans le même système.
Notez que le courant de fréquence fondamentale (60 Hz, ou la 1ère harmonique) est pratiquement absent du conducteur neutre. Notre analyse de Fourier ne montre que 0,4337 µA de 1ère harmonique lors de la lecture de la tension aux bornes de Rneutre . La même chose peut être dite à propos des 5e et 7e harmoniques, ces deux courants ayant une amplitude négligeable.
En revanche, les 3e et 9e harmoniques sont fortement représentées dans le conducteur neutre, avec 149,3 mA (1,493E-01 volts sur 1 ) chacune ! C'est très près de 150 mA, soit trois fois les valeurs des sources de courant, individuellement.
Avec trois sources par fréquence harmonique dans la charge, il semble que nos courants de 3e et 9e harmoniques dans chaque phase s' ajoutent pour former le courant neutre. Voir Analyse de Fourier :« Composantes de Fourier de la réponse transitoire v(0,7) »
Analyse graphique du domaine temporel
C'est exactement ce qui se passe, même s'il n'est peut-être pas évident de comprendre pourquoi.
La clé pour comprendre cela est clairement indiquée dans un graphique dans le domaine temporel des courants de phase. Examinez ce tracé des courants de phase équilibrés au fil du temps, avec une séquence de phases de 1-2-3. (Figure ci-dessous)
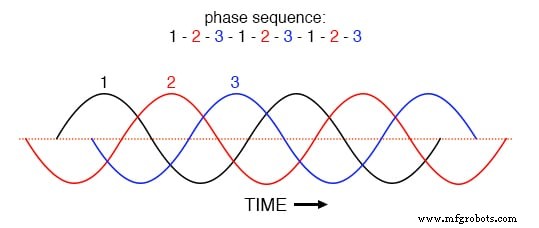
Séquence de phases 1-2-3-1-2-3-1-2-3 d'ondes également espacées.
Avec les trois formes d'onde fondamentales également décalées sur l'axe des temps du graphique, il est facile de voir comment elles s'annuleraient pour donner un courant résultant nul dans le conducteur neutre. Considérons, cependant, à quoi ressemblerait une forme d'onde de 3e harmonique pour la phase 1 superposée sur le graphique de la figure ci-dessous.
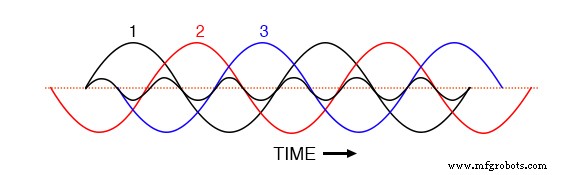
La troisième forme d'onde harmonique pour la phase 1 superposée aux formes d'onde fondamentales triphasées.
Observez comment cette forme d'onde harmonique a la même relation de phase avec les 2ème et 3ème formes d'onde fondamentales qu'avec la 1ère :dans chaque demi-cycle positif de tout des formes d'onde fondamentales, vous trouverez exactement deux demi-cycles positifs et un demi-cycle négatif de la forme d'onde harmonique.
Cela signifie que les formes d'onde de 3e harmonique de trois formes d'onde de fréquence fondamentale déphasées de 120 ° sont en fait en phase avec l'un l'autre. Le chiffre de déphasage de 120° généralement supposé dans les systèmes à courant alternatif triphasé ne s'applique qu'aux fréquences fondamentales, pas à leurs multiples harmoniques !
Si nous devions tracer les trois formes d'onde de la 3e harmonique sur le même graphique, nous les verrions se chevaucher précisément et apparaître comme une seule forme d'onde unifiée (indiquée en gras dans (Figure ci-dessous)
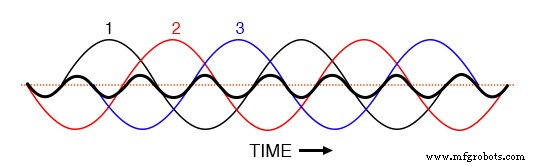
Les troisièmes harmoniques des phases 1, 2, 3 coïncident toutes lorsqu'elles sont superposées aux formes d'onde triphasées fondamentales.
Analyse mathématique du graphique du domaine temporel
Pour les plus mathématiques, ce principe peut être exprimé symboliquement. Supposons que A représente une forme d'onde et B un autre, tous deux à la même fréquence, mais décalés de 120° l'un de l'autre en termes de phase. Appelons la 3e harmonique de chaque forme d'onde A' et B' , respectivement.
Le déphasage entre A’ et B' n'est pas de 120° (c'est le déphasage entre A et B ), mais 3 fois plus, car le A’ et B' les formes d'onde alternent trois fois plus vite que A et B . Le décalage entre les formes d'onde n'est exprimé avec précision qu'en termes d'angle de phase lorsque la même vitesse angulaire est supposée.
Lors de la mise en relation de formes d'onde de fréquences différentes, la façon la plus précise de représenter le déphasage est en termes de temps; et le décalage temporel entre A’ et B' équivaut à 120° à une fréquence trois fois inférieure, ou 360° à la fréquence de A’ et B' . Un déphasage de 360° équivaut à un déphasage de 0°, c'est-à-dire aucun déphasage du tout.
Ainsi, A’ et B' doivent être en phase les uns avec les autres :
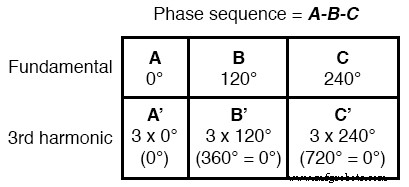
Cette caractéristique de la 3e harmonique dans un système triphasé est également vraie pour tout multiple entier de la 3e harmonique.
Ainsi, non seulement les 3e formes d'onde harmoniques de chaque forme d'onde fondamentale sont en phase les unes avec les autres, mais aussi les 6e harmoniques, les 9e harmoniques, les 12e harmoniques, les 15e harmoniques, les 18e harmoniques, les 21e harmoniques, et ainsi de suite.
Étant donné que seules les harmoniques impaires apparaissent dans les systèmes où la distorsion de la forme d'onde est symétrique par rapport à la ligne centrale - et la plupart des charges non linéaires créent une distorsion symétrique - les multiples pairs de la 3e harmonique (6e, 12e, 18e, etc.) ne sont généralement pas significatifs, ne laissant que le des multiples impairs (3e, 9e, 15e, 21e, etc.) pour contribuer de manière significative aux courants neutres.
Dans les systèmes d'alimentation polyphasés avec un certain nombre de phases autre que trois, cet effet se produit avec des harmoniques du même multiple. Par exemple, les courants harmoniques qui s'ajoutent au conducteur neutre d'un système à 4 phases connecté en étoile où le déphasage entre les formes d'onde fondamentales est de 90° seraient les 4e, 8e, 12e, 16e, 20e, et ainsi de suite.
Triple Harmoniques
En raison de leur abondance et de leur importance dans les systèmes électriques triphasés, la 3e harmonique et ses multiples ont leur propre nom spécial :triplen harmoniques .
Tous les harmoniques triples s'additionnent dans le conducteur neutre d'une charge connectée en Y à 4 fils. Dans les systèmes d'alimentation contenant une charge non linéaire substantielle, les courants harmoniques triples peuvent être d'une amplitude suffisamment élevée pour provoquer une surchauffe des conducteurs neutres.
Ceci est très problématique, car d'autres problèmes de sécurité interdisent aux conducteurs neutres d'avoir une protection contre les surintensités, et il n'y a donc aucune disposition pour l'interruption automatique de ces courants élevés.
Analyse des effets des harmoniques triples dans un circuit Y-Y
L'illustration suivante montre comment les courants harmoniques triples créés à la charge s'ajoutent dans le conducteur neutre. Le symbole « ω » est utilisé pour représenter la vitesse angulaire et est mathématiquement équivalent à 2πf. Ainsi, « ω » représente la fréquence fondamentale, « 3ω » représente le 3e harmonique, « 5ω » représente le 5e harmonique, et ainsi de suite :(Figure ci-dessous)
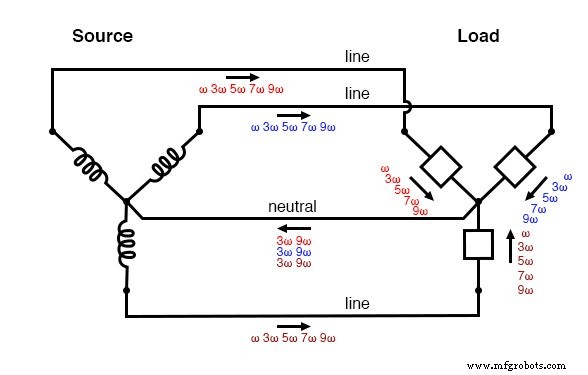
« Y-Y » Triple source/charge :les courants harmoniques s'ajoutent au conducteur neutre.
Dans un effort pour atténuer ces courants triples additifs, on pourrait être tenté de supprimer entièrement le fil neutre. If there is no neutral wire in which triplen currents can flow together, then they won’t, right?
Unfortunately, doing so just causes a different problem:the load’s “Y” center-point will no longer be at the same potential as the source’s, meaning that each phase of the load will receive a different voltage than what is produced by the source.
We’ll re-run the last SPICE simulation without the 1 Ω Rneutral resistor and see what happens:
Y-Y source/load (no neutral) with harmonics * * phase1 voltage source and r (120 v / 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v / 120 deg) vsource2 3 0 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v / 240 deg) vsource3 5 0 sin(0 120 60 11.1111m 0) rsource3 5 6 1 * * line resistances rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 0 0) i5har1 8 7 sin(0 50m 300 0 0) i7har1 8 7 sin(0 50m 420 0 0) i9har1 8 7 sin(0 50m 540 0 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 5.55555m 0) i5har2 9 7 sin(0 50m 300 5.55555m 0) i7har2 9 7 sin(0 50m 420 5.55555m 0) i9har2 9 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 11.1111m 0) i5har3 10 7 sin(0 50m 300 11.1111m 0) i7har3 10 7 sin(0 50m 420 11.1111m 0) i9har3 10 7 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 12m 1u .plot tran v(2,8) .four 60 v(2,8) .plot tran v(0,7) .four 60 v(0,7) .plot tran v(8,7) .four 60 v(8,7) .finir
Fourier analysis of line current:
Fourier components of transient response v(2,8) dc component =5.423E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 0.000 0.000 2 1.200E+02 2.388E-10 0.000000 158.016 158.016 3 1.800E+02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E+02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E+02 4.990E-02 0.416665 0.000 0.000 6 3.600E+02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E+02 4.990E-02 0.416668 0.000 0.000 8 4.800E+02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E+02 9.406E-07 0.000008 -90.005 -90.005 total harmonic distortion =58.925539 percent
Fourier analysis of voltage between the two “Y” center-points:
Fourier components of transient response v(0,7) dc component =6.093E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.453E-04 1.000000 60.018 0.000 2 1.200E+02 6.263E-08 0.000431 91.206 31.188 3 1.800E+02 5.000E+01 344147.7879 -180.000 -240.018 4 2.400E+02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E+02 3.023E-04 2.080596 119.981 59.963 6 3.600E+02 1.138E-07 0.000783 15.882 -44.136 7 4.200E+02 4.234E-04 2.913955 59.993 -0.025 8 4.800E+02 2.001E-07 0.001378 35.584 -24.434 9 5.400E+02 5.000E+01 344147.4728 -179.999 -240.017 total harmonic distortion =************ percent
Fourier analysis of load phase voltage:
Fourier components of transient response v(8,7) dc component =6.070E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 0.000 0.000 2 1.200E+02 6.231E-08 0.000000 90.473 90.473 3 1.800E+02 5.000E+01 0.417500 -180.000 -180.000 4 2.400E+02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E+02 9.995E-02 0.000835 179.850 179.850 6 3.600E+02 1.023E-07 0.000000 13.485 13.485 7 4.200E+02 9.959E-02 0.000832 179.790 179.789 8 4.800E+02 1.991E-07 0.000000 35.462 35.462 9 5.400E+02 5.000E+01 0.417499 -179.999 -179.999 total harmonic distortion =59.043467 percent
Strange things are happening, indeed.
First, we see that the triplen harmonic currents (3rd and 9th) all but disappear in the lines connecting a load to source. The 5th and 7th harmonic currents are present at their normal levels (approximately 50 mA), but the 3rd and 9th harmonic currents are of negligible magnitude.
Second, we see that there is a substantial harmonic voltage between the two “Y” center-points, between which the neutral conductor used to connect. According to SPICE, there are 50 volts of both 3rd and 9th harmonic frequency between these two points, which is definitely not normal in a linear (no harmonics), balanced Y system.
Finally, the voltage as measured across one of the load’s phases (between nodes 8 and 7 in the SPICE analysis) likewise shows strong triplen harmonic voltages of 50 volts each.
The figure below is a graphical summary of the aforementioned effects.
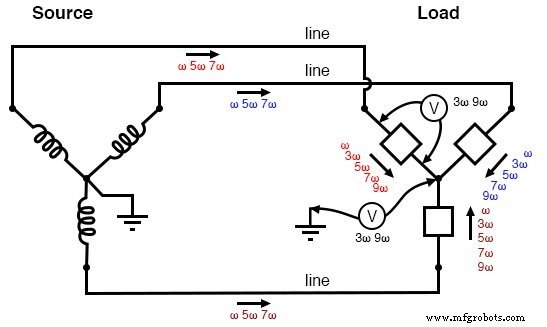
Three-wire “Y-Y” (no neutral) system:Triplen voltages appear between “Y” centers. Triplen voltages appear across load phases. Non-triplen currents appear in line conductors.
In summary, removal of the neutral conductor leads to a “hot” center-point on the load “Y”, and also to harmonic load phase voltages of equal magnitude, all comprised of triplen frequencies.
In the previous simulation where we had a 4-wire, Y-connected system, the undesirable effect from harmonics was excessive neutral current , but at least each phase of the load received voltage nearly free of harmonics.
Analysis of the Effects of Triplen Harmonics in a Delta-Wye(Y) Circuit
Since removing the neutral wire didn’t seem to work in eliminating the problems caused by harmonics, perhaps switching to a Δ configuration will. Let’s try a Δ source instead of a Y, keeping the load in its present Y configuration, and see what happens.
The measured parameters will be line current (voltage across Rline , nodes 0 and 8), load phase voltage (nodes 8 and 7), and source phase current (voltage across Rsource , nodes 1 and 2). (Figure ci-dessous)
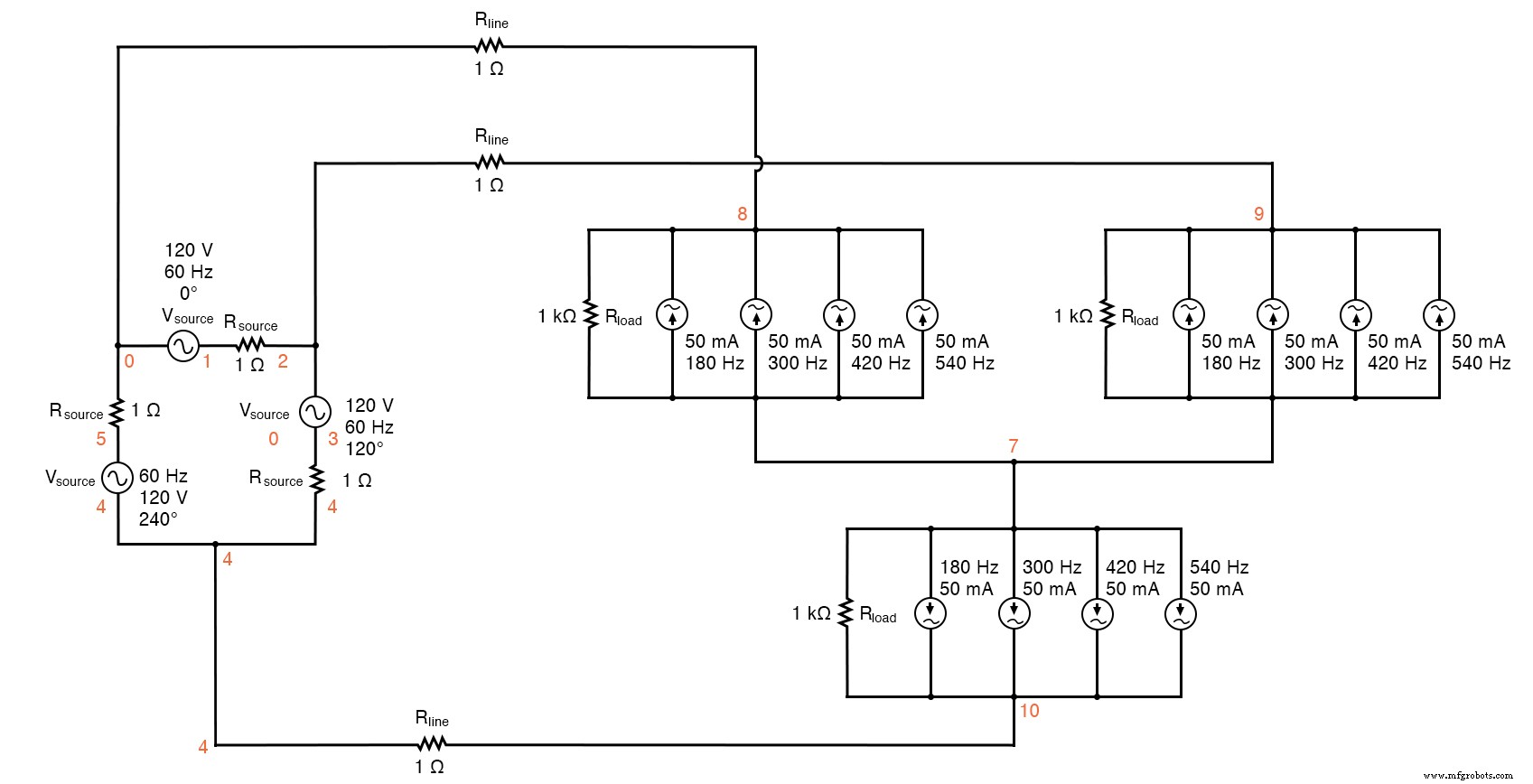
Delta-Y source/load with harmonics
Delta-Y source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 207.846 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 207.846 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * phase 1 of load rload1 8 7 1k i3har1 8 7 sin(0 50m 180 9.72222m 0) i5har1 8 7 sin(0 50m 300 9.72222m 0) i7har1 8 7 sin(0 50m 420 9.72222m 0) i9har1 8 7 sin(0 50m 540 9.72222m 0) * * phase 2 of load rload2 9 7 1k i3har2 9 7 sin(0 50m 180 15.2777m 0) i5har2 9 7 sin(0 50m 300 15.2777m 0) i7har2 9 7 sin(0 50m 420 15.2777m 0) i9har2 9 7 sin(0 50m 540 15.2777m 0) * * phase 3 of load rload3 10 7 1k i3har3 10 7 sin(0 50m 180 4.16666m 0) i5har3 10 7 sin(0 50m 300 4.16666m 0) i7har3 10 7 sin(0 50m 420 4.16666m 0) i9har3 10 7 sin(0 50m 540 4.16666m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,8) v(8,7) v(1,2) .four 60 v(0,8) v(8,7) v(1,2) .finir
Note:the following paragraph is for those curious readers who follow every detail of my SPICE netlists. If you just want to find out what happens in the circuit, skip this paragraph!
When simulating circuits having AC sources of differing frequency and differing phase, the only way to do it in SPICE is to set up the sources with a delay time or phase offset specified in seconds. Thus, the 0° source has these five specifying figures:“(0 207.846 60 0 0)”, which means 0 volts DC offset, 207.846 volts peak amplitude (120 times the square root of three, to ensure the load phase voltages remain at 120 volts each), 60 Hz, 0 time delay, and 0 damping factor.
The 120° phase-shifted source has these figures:“(0 207.846 60 5.55555m 0)”, all the same as the first except for the time delay factor of 5.55555 milliseconds, or 1/3 of the full period of 16.6667 milliseconds for a 60 Hz waveform.
The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.
This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.
If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.
This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).
One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.
The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.
Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:
Fourier analysis of line current:
Fourier analysis of load phase voltage:
Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent
Fourier analysis of source phase current:
Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent
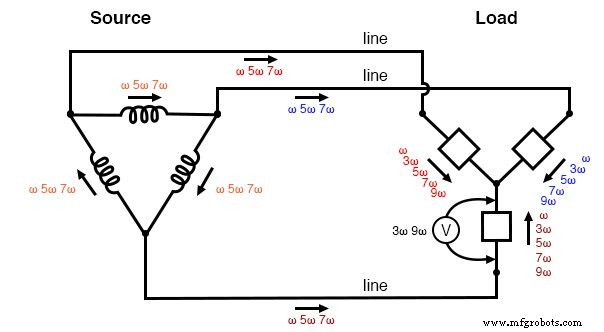
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.
Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.
Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit
If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.
The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.
It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.
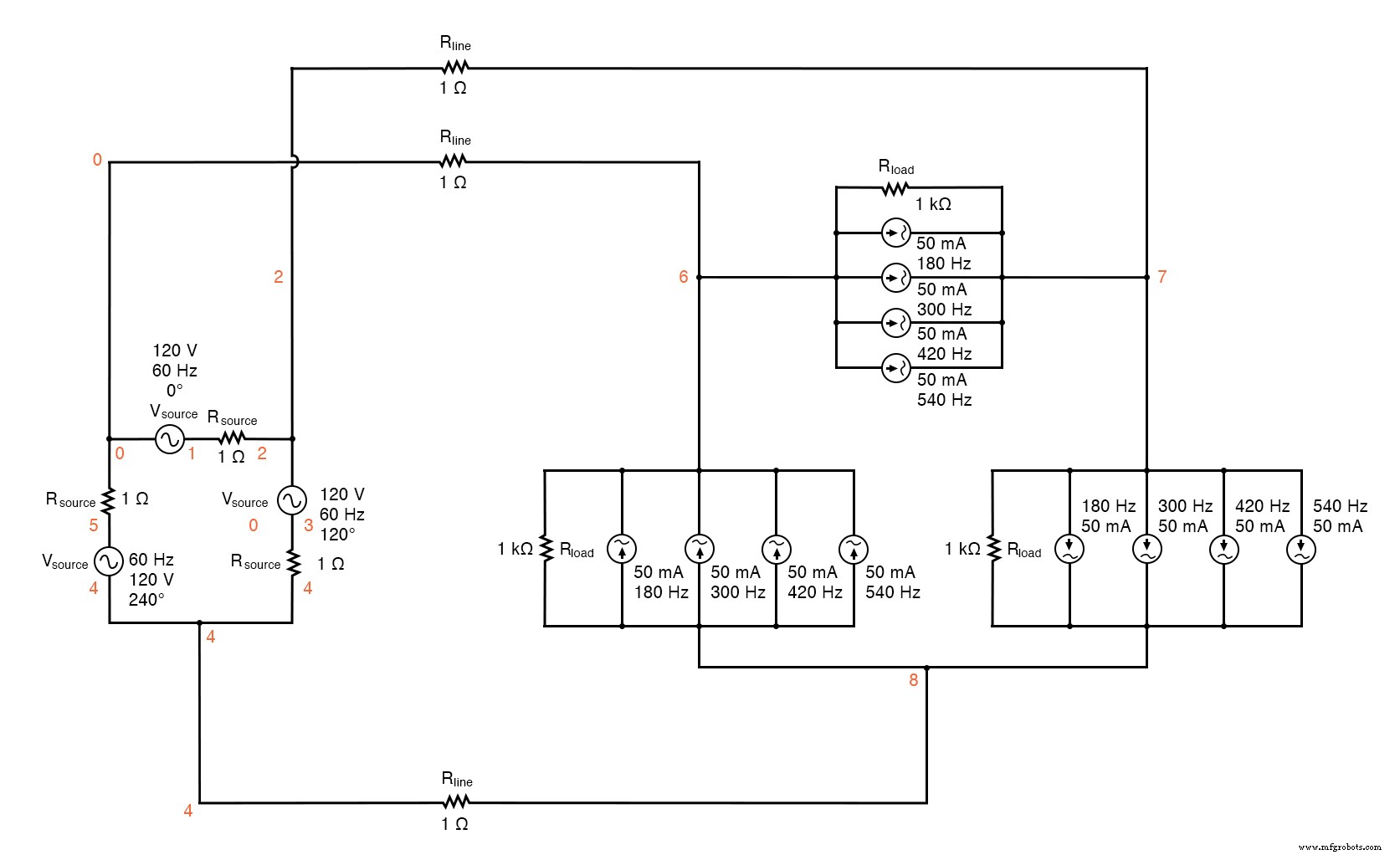
Delta-Delta source/load with harmonics.
Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .finir
Fourier analysis of line current:
Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent
Fourier analysis of load phase voltage:
Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent
Fourier analysis of source phase current:
Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent
As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.
But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?
Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit
Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.
Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.
What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.
These results may be graphically summarized as such in the figure below.
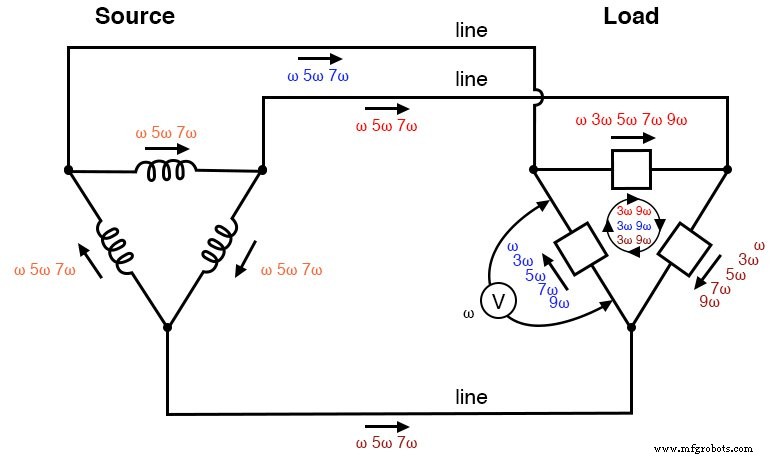
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.
This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.
AVIS :
- Nonlinear components are those that draw a non-sinusoidal (non-sine-wave) current waveform when energized by a sinusoidal (sine-wave) voltage. Since any distortion of an originally pure sine-wave constitutes harmonic frequencies, we can say that nonlinear components generate harmonic currents.
- When the sine-wave distortion is symmetrical above and below the average centerline of the waveform, the only harmonics present will be odd-numbered , not even-numbered.
- The 3rd harmonic, and integer multiples of it (6th, 9th, 12th, 15th) are known as triplen harmonics. They are in phase with each other, despite the fact that their respective fundamental waveforms are 120° out of phase with each other.
- In a 4-wire Y-Y system, triplen harmonic currents add within the neutral conductor.
- Triplen harmonic currents in a Δ-connected set of components circulate within the loop formed by the Δ.
FICHES DE TRAVAIL CONNEXES :
- Fiche de travail sur les signaux à fréquence mixte
Technologie industrielle
- Introduction aux circuits CA
- Systèmes de numération
- Relais de protection
- Calculs de puissance
- Systèmes de signalisation actuels
- Un système de refroidissement passif peu coûteux qui ne nécessite aucune alimentation
- Introduction aux harmoniques :partie 2
- Introduction aux harmoniques :Partie 1
- Quels sont les principaux types de systèmes de transmission de puissance mécanique ?



