Qu'est-ce que la transformée de Fourier ?

Cet article vous donne des informations essentielles sur une technique mathématique qui joue un rôle absolument fondamental dans la conception du système et le traitement du signal.

Nommée d'après le mathématicien français Joseph Fourier, la transformée de Fourier est une procédure mathématique qui nous permet de déterminer le contenu fréquentiel d'une fonction. Pour les ingénieurs électriciens, la transformée de Fourier est généralement appliquée aux fonctions du temps que nous appelons signaux .

Décomposition sinusoïdale

Un tracé de tension ou de courant en fonction du temps, comme nous le verrions sur un écran d'oscilloscope, est une représentation intuitive du comportement du signal. Ce n'est cependant pas la seule représentation utile.

Dans de nombreux cas, par exemple dans la conception de systèmes RF, nous nous intéressons principalement au comportement périodique des signaux. Plus précisément, nous nous intéressons à la compréhension d'un signal par rapport à sinusoïdal périodicité, car les sinusoïdes sont l'expression mathématique unique de la fréquence « pure ».

La transformée de Fourier révèle la périodicité élémentaire d'un signal en décomposant le signal en ses fréquences sinusoïdales constitutives et en identifiant les amplitudes et les phases de ces fréquences constitutives.

Le mot « décomposition » est ici crucial. La transformée de Fourier nous apprend à considérer un signal dans le domaine temporel comme une forme d'onde composée de formes d'onde sinusoïdales sous-jacentes avec diverses amplitudes et phases.

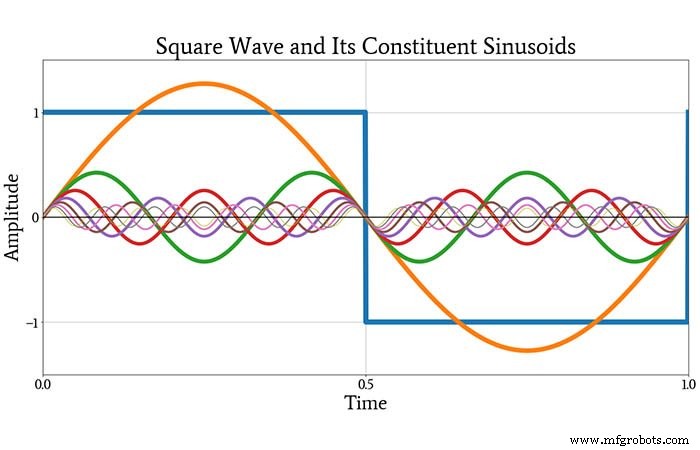
Une onde carrée, par exemple, peut être décomposée en une série infinie de sinusoïdes avec des amplitudes qui diminuent régulièrement et des fréquences qui augmentent régulièrement. La série exacte, pour une onde carrée couplée en courant alternatif de période T et d'amplitude A, peut être écrite comme suit :

\[f_{square}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\ }}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]

Nous pouvons convertir cela sous la forme suivante, qui est un peu plus intuitive :

\[f_{square}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3 }\sin(6\pi pi)+\frac{1}{5}\sin(10\pi pi)+\ ...\right)\]

où f est la fréquence, en hertz, de l'onde carrée.

Le graphique suivant montre l'onde carrée d'origine, en bleu, et les huit premières sinusoïdes de la série infinie.

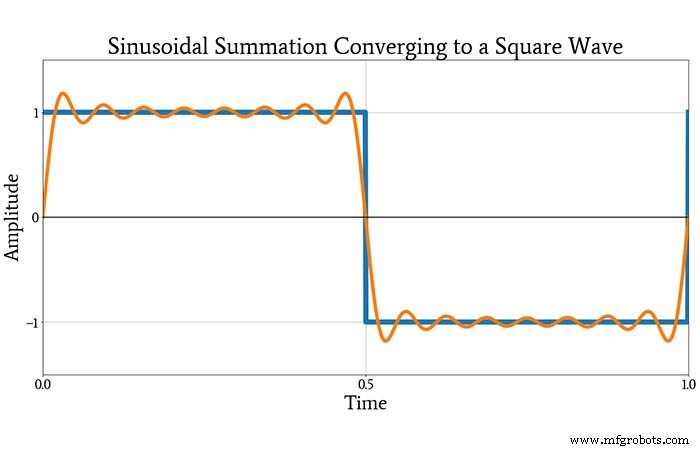
Après avoir regardé ce tracé, vous pourriez encore être un peu sceptique quant à la possibilité de combiner ces sinusoïdes en une onde carrée. La prochaine intrigue vous convaincra, cependant. Il montre l'onde carrée d'origine et la forme d'onde produite par ajout toutes les sinusoïdes constitutives indiquées ci-dessus.

Fonctions du temps et de la fréquence

Lorsque nous calculons une transformée de Fourier, nous commençons par une fonction du temps, f(t), et par décomposition mathématique, nous produisons une fonction de fréquence, F(ω). (Nous utilisons généralement la fréquence angulaire dans les discussions théoriques sur la transformée de Fourier.)

L'évaluation de F(ω) à une fréquence angulaire spécifique, disons 100 rad/s, nous donne l'amplitude et la phase de la composante sinusoïdale de f(t) qui a une fréquence de 100 rad/s. Si f(t) n'a pas de composante sinusoïdale à 100 rad/s, la magnitude sera nulle.

Vous vous demandez peut-être comment une fonction, F(ω), peut rendre compte à la fois de l'amplitude et de la phase. La transformée de Fourier produit une valeur complexe fonction, ce qui signifie que la transformée elle-même n'est ni l'amplitude des composantes de fréquence dans f(t) ni la phase de ces composantes. Comme pour tout nombre complexe, nous devons effectuer des calculs supplémentaires pour extraire la magnitude ou la phase.

Le concept de transformation à valeur complexe est un peu plus intuitif lorsque nous travaillons avec un discret Transformée de Fourier, plutôt qu'une transformée « standard » dans laquelle on commence par une fonction symbolique du temps et on finit par une fonction symbolique de la fréquence.

La transformée de Fourier discrète opère sur une séquence de valeurs numériques et produit une séquence de coefficients de Fourier . Ces coefficients sont des nombres complexes typiques (c'est-à-dire qu'ils ont la forme a + jb), et nous utilisons généralement la magnitude de ces nombres complexes, calculée comme √(a ² +b ² ), lors de l'analyse du contenu fréquentiel d'un signal.

Tracé de la transformée de Fourier

Les tracés de contenu fréquentiel sont extrêmement courants dans les fiches techniques, les rapports de test, les manuels, etc. Nous nous référons souvent à un tracé de magnitude en fonction de la fréquence en tant que spectre - par exemple, " examinons le spectre du signal " signifie " examinons une sorte de représentation visuelle des informations de magnitude dans la transformée de Fourier ."

Le graphique suivant montre le spectre d'une onde carrée couplée en courant alternatif avec une amplitude de 1 et une fréquence de 1 Hz.

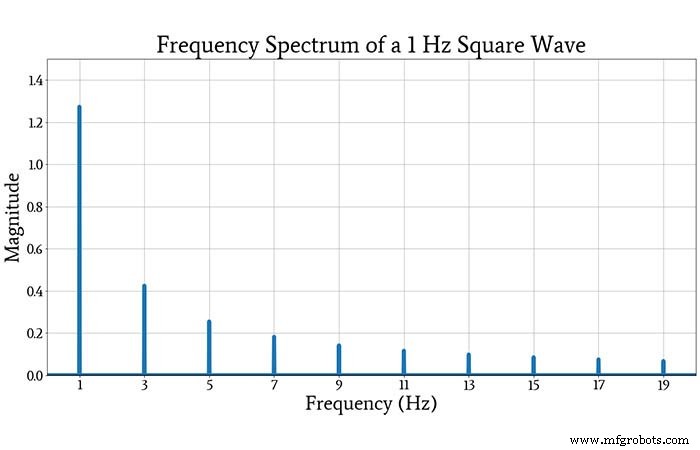
Si vous comparez les amplitudes tracées des "pics" de fréquence aux amplitudes des composantes sinusoïdales correspondantes dans la série infinie discutée ci-dessus, vous verrez qu'elles sont cohérentes.

Calcul de la transformée de Fourier

Nous sommes presque à la fin de cet article, et je ne vous ai toujours pas expliqué comment nous générons réellement la transformée de Fourier d'un signal mathématiquement défini.

Pour être honnête, je ne vois pas la nécessité d'explorer en profondeur les détails mathématiques dans un article d'introduction :l'analyse du domaine fréquentiel est aujourd'hui dominée par des techniques logicielles conviviales, et les ingénieurs ne passent pas beaucoup de temps à convertir le temps symbolique. expressions du domaine en expressions symboliques du domaine fréquentiel.

Néanmoins, avec quelque chose d'aussi important que la transformée de Fourier, il est bon d'être au moins conscient des mathématiques sous-jacentes. Alors, sans plus tarder, voici comment nous convertissons f(t) en F(ω) :

\[F(\omega ) =\int\limits_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t} }dt}\]

Conclusion

J'espère que cet article a fourni une explication claire et intuitive de ce qu'est la transformée de Fourier et comment elle nous donne un aperçu supplémentaire de la nature d'un signal.

La transformée de Fourier n'est que le début d'un vaste éventail de sujets connexes ; si vous souhaitez en savoir plus, consultez les articles ci-dessous.

Lectures complémentaires

• Une introduction à la transformée de Fourier discrète
• Une introduction à la transformée de Fourier rapide
• Comment effectuer une analyse de domaine de fréquence avec Scilab
• Apprendre à vivre dans le domaine fréquentiel
• Filtrage linéaire basé sur la transformée de Fourier discrète