Dérivés des fonctions de puissance de e

Exemple de dérivés de e

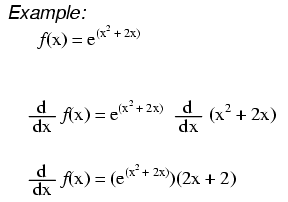
Constante de proportionnalité

Lorsque nous disons qu'une relation ou un phénomène est « exponentiel », nous sous-entendons qu'une certaine quantité – courant électrique, profits, population – augmente plus rapidement à mesure que la quantité augmente. En d'autres termes, le taux de variation par rapport à une variable donnée est proportionnel à la valeur de cette variable. Cela signifie que la dérivée d'une fonction exponentielle est égale à la fonction exponentielle d'origine multipliée par une constante (k ) qui établit la proportionnalité.

$$\frac{\text{d}}{\text{d}x}a^x=ka^x$$

La constante de proportionnalité est égale au logarithme naturel de la base de l'exposant :

$$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$

Il s'ensuit donc que si le logarithme naturel de la base est égal à un, la dérivée de la fonction sera égale à la fonction d'origine. C'est exactement ce qui se passe avec les fonctions puissance de e :le logarithme naturel de e est 1, et par conséquent, la dérivée de $$e^x$$ est $$e^x$$.

$$\frac{\text{d}}{\text{d}x}e^x=e^x$$

La règle de la "chaîne"

Lorsque l'expression exponentielle est autre chose que simplement x, nous appliquons la règle de la chaîne :d'abord nous prenons la dérivée de l'expression entière, puis nous la multiplions par la dérivée de l'expression dans l'exposant.

$$\frac{\text{d}}{\text{d}x}e^{x^2+2x}=e^{x^2+2x}\times\frac{\text{d}}{ \text{d}x}(x^2+2x)=(2x+2)e^{x^2+2x}$$

Cette technique peut être utilisée pour trouver le taux de variation du courant de diode par rapport à la tension de diode. L'équation suivante fournit une relation approximative entre la tension aux bornes d'une diode ($$V_D$$) et le courant à travers une diode ($$I_D$$) :

$$I_D=I_S\times e^\frac{V_D}{0.026}$$

(Voir la page sur les diodes et les redresseurs pour plus d'informations sur l'équation courant-tension de la diode; notez également que $$I_S$$ est une constante, pas une variable.) Pour trouver le taux de variation du courant par rapport à la tension, on prend la dérivée :

$$\frac{\text{d}I_D}{\text{d}V_D}=\frac{\text{d}}{\text{d}V_D}(I_S\times e^\frac{V_D}{ 0.026})=I_S\times e^\frac{V_D}{0.026}\times\frac{1}{0.026}$$

Ainsi, à une valeur donnée de tension de diode $$V_D$$, une augmentation incrémentale de tension créera une augmentation de courant égale à $$\frac{I_S}{0.026}e^\frac{V_D}{0.026}$$ .

FICHES DE TRAVAIL CONNEXES :

• Feuille de calcul pour les circuits électriques