Description des circuits combinés dans Verilog

06 janvier 2019 par le Dr Steve Arar

Cet article présente les techniques de description des circuits combinatoires dans Verilog en examinant comment utiliser l'opérateur conditionnel pour décrire les tables de vérité combinatoire.

Cet article présente les techniques de description des circuits combinatoires dans Verilog en examinant comment utiliser l'opérateur conditionnel pour décrire les tables de vérité combinatoires. Il montre également comment utiliser le bloc Verilog « toujours » pour décrire des circuits combinatoires. Un bloc « toujours » peut nous fournir une solution encore plus simple pour décrire un circuit numérique.

Dans un article précédent, nous avons parlé de l'utilisation du mot-clé « assign » de Verilog pour effectuer une affectation continue. De telles affectations sont toujours actives et peuvent être utilisées pour acquérir une description au niveau de la porte des circuits numériques. Par exemple, dans le code suivant, qui décrit une porte ET, le membre de droite est évalué en continu et le résultat est mis sur le réseau out1 :

assign out1 =a &b;  

Verilog a un opérateur conditionnel (?:) qui nous permet de vérifier une condition avant de faire de telles affectations. La syntaxe est donnée ci-dessous :

assigner [nom_signal] =[expression_conditionnelle] ? [value_if_true] :[value_if_false] ; 

L'« expression_conditionnelle » est évaluée. Si c'est vrai, "value_if_true" est assigné à "signal_name". Si ce n'est pas vrai, "signal_name" obtient "value_if_false". À titre d'exemple, considérons le code suivant :

assign out1 =(sel) ? (a &b) :(a|b); 

Si "sel" est vrai, a&b sera assigné à "out1". Si ce n'est pas vrai, "out1" obtiendra a|b. Par conséquent, le code ci-dessus implémente la fonctionnalité d'un multiplexeur 2 vers 1. L'implémentation conceptuelle de ce code peut être comme illustré dans la figure 1 ci-dessous.

L'affectation conditionnelle nous permet d'avoir une description plus abstraite de certains circuits car elle a la fonctionnalité d'une déclaration « si » trouvée dans les langages de programmation informatiques traditionnels. L'opérateur conditionnel peut être utilisé sous une forme imbriquée pour implémenter des circuits plus complexes. L'exemple 1 traite de ces détails.

Exemple 1 : opérateurs conditionnels imbriqués

Utilisez l'opérateur conditionnel (?:) pour décrire un codeur de priorité 4 à 2 avec la table de vérité suivante :

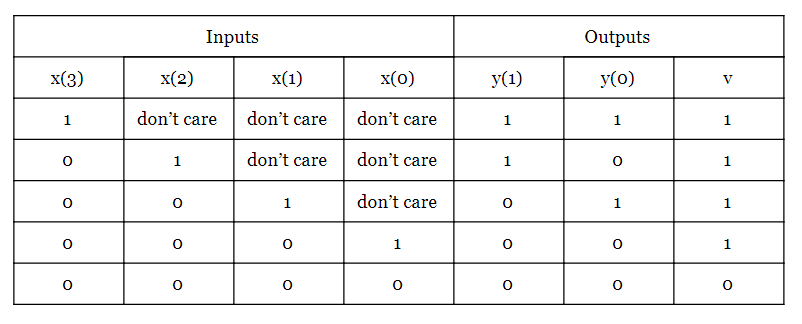
Le code Verilog de cet encodeur prioritaire est donné ci-dessous :

 module Prio_4_to_2 ( fil d'entrée [3:0] x, fil de sortie [1:0] y, fil de sortie v ); assigner y =x[3] ? 2'b11 :x[2] ? 2'b10 :x[1] ? 2'b01 :2'b00 ; assigner v =( x[3] | x[2] | x[1] | x[0] ) ? 1'b1 :1'b0 ; module de fin 

Outre les lignes 7 à 10, le code contient les éléments de base du langage discutés dans notre article précédent. Jetons donc un œil à ces lignes.

Les termes 2'b11, 2'b10, 2'b01 font référence aux notations Verilog qui représentent des nombres binaires à deux bits. En général, le premier nombre (avant ‘b) spécifie le nombre de bits. La lettre b précise que les nombres sont binaires. Les chiffres après 'b donnent la valeur du nombre. Par conséquent, 2'b01 est la notation Verilog pour représenter un nombre binaire à deux bits avec la valeur 01 et 3'b100 désigne un nombre binaire à trois bits avec la valeur 100.

La ligne 7 vérifie le MSB de l'entrée, x[3], dans un opérateur conditionnel. Si x[3]=1, la condition est évaluée comme vraie et 2'b11 est affecté à y (la valeur affectée est tirée de la table de vérité). Si x[3]=0, la condition est évaluée comme fausse et l'expression après les deux points (:) sera affectée à y. L'expression après les deux points est le code de la ligne 8 qui est lui-même un autre opérateur conditionnel.

Le deuxième opérateur conditionnel de la ligne 8 examine le deuxième bit le plus significatif de l'entrée, x[2], pour déterminer si 2'b10 doit être affecté à y ou l'expression après les deux points qui est à nouveau un autre opérateur conditionnel (ligne 9) doit être évalué. Vous pouvez vérifier que les valeurs attribuées à y correspondent à la table de vérité donnée.

La sortie valide (v) de la table de vérité sera au niveau logique haut si au moins un bit de l'entrée est au niveau logique haut. La ligne 11 montre cette description en appliquant l'opérateur OU au niveau du bit (|) aux bits de l'entrée. Une simulation Xilinx ISE du code ci-dessus est illustrée à la figure 2.

Figure 2. Une simulation Xilinx ISE à partir du code ci-dessus.

Il est important de noter que les expressions conditionnelles sont évaluées successivement jusqu'à ce qu'une expression vraie soit trouvée. L'affectation correspondant à cette expression vraie sera effectuée. En conséquence, les expressions évaluées précédemment ont une priorité plus élevée par rapport aux suivantes. Cela signifie que, théoriquement, un opérateur conditionnel est plus adapté à la mise en œuvre d'un réseau prioritaire (figure 3) qu'une structure équilibrée telle qu'un multiplexeur (figure 4).

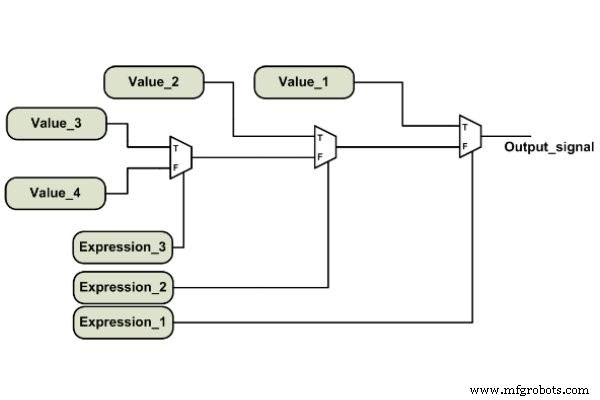
Figure 3. Un réseau prioritaire.

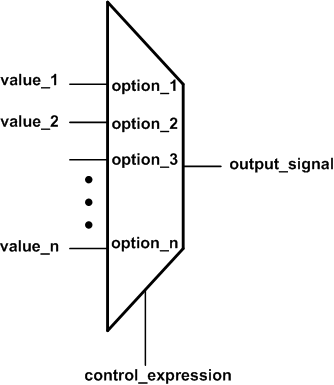
Figure 4. Un multiplexeur n-à-1 dans lequel il n'y a pas de priorité entre les entrées.

Un article précédent révèle une discussion similaire sur les affectations simultanées VHDL.

Déclarations de procédure Verilog

Nous pouvons séparer n'importe quel circuit combinatoire en quelques portes logiques de base (ET, OU, NON, etc.) et utiliser l'instruction « assign » pour décrire ces portes (une description au niveau de la porte). Nous pouvons également utiliser l'opérateur conditionnel discuté dans la section précédente pour avoir une manière plus abstraite de décrire certains circuits combinatoires (similaire à l'instruction "if" des langages de programmation informatique). Cependant, il existe encore une solution plus puissante :utiliser le bloc Verilog « always ».

À l'intérieur d'un bloc « always », nous pouvons avoir des instructions procédurales exécutées en séquence. De plus, le bloc "always" prend en charge les constructions de langage abstrait telles que les instructions "if" et "case".

La fonction d'exécution séquentielle ainsi que les constructions de langage abstrait disponibles dans un bloc "toujours" nous permettent de décrire plus facilement la fonctionnalité d'un circuit, du fait que le raisonnement humain a une nature séquentielle et repose sur des descriptions abstraites. Nous pensons généralement de manière algorithmique de haut niveau plutôt qu'en termes de portes logiques de bas niveau. Un bloc « toujours » peut nous fournir une solution plus simple pour décrire un circuit numérique. Pour plus de détails sur les raisons pour lesquelles les HDL prennent en charge les descriptions basées sur des instructions séquentielles, veuillez consulter mon article Introduction aux instructions VHDL séquentielles.

Exemple 2 : instructions de blocage « Toujours »

La syntaxe simplifiée d'un bloc « always » est donnée ci-dessous :

always @(sensibility_list) begin séquentiel_statements ; fin 

La liste_sensibilité spécifie quand les instructions séquentielles à l'intérieur du bloc « always » doivent être exécutées. Par exemple, envisagez d'utiliser le bloc « toujours » pour décrire le circuit de la figure 5.

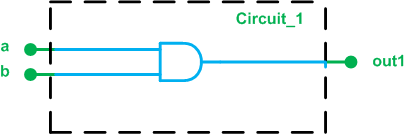
Figure 5. Circuit_1

Lorsque a ou b change, la sortie peut changer, ce qui signifie que a et b doivent être dans la liste de sensibilité du bloc « toujours ». En général, pour un circuit combinatoire, tous les signaux d'entrée doivent être inclus dans la liste de sensibilité.

Maintenant, nous pouvons utiliser l'opérateur ET au niveau du bit pour décrire la fonctionnalité du circuit (a&b) et affecter le résultat à la sortie. Au sein d'un bloc « toujours », il existe deux types d'affectations différents :l'affectation bloquante (=) et l'affectation non bloquante (<=). En utilisant l'affectation bloquante, nous obtenons le code suivant :

toujours @(a, b)begin out1 =a &b;end 

Quelle est la différence entre une affectation bloquante et une affectation non bloquante ?

Avec une affectation bloquante, le côté droit est évalué et immédiatement affecté à out1. Par conséquent, lorsque la ligne 3 est exécutée, out1 est immédiatement mis à jour avant de passer à la ligne suivante du code. Le nom « affectation bloquante » souligne que les lignes à venir sont bloquées jusqu'à ce que le côté gauche soit mis à jour.

Avec une affectation non bloquante, l'expression de droite est évaluée mais elle n'est pas appliquée à la variable de gauche tant que nous n'avons pas atteint la fin du bloc « toujours ». Le choix d'une affectation bloquante ou non bloquante peut être déroutant pour un débutant et une mauvaise utilisation de celles-ci peut conduire à une fonctionnalité indésirable. Par exemple, l'utilisation d'affectations bloquantes pour déduire des bascules peut introduire une condition de concurrence.

Pour cet article d'introduction, nous n'entrerons pas plus dans les détails et nous nous en tiendrons à une seule règle simple pour éviter les pièges potentiels :utilisez les affectations bloquantes lors de l'écriture du code d'un circuit combinatoire. Par conséquent, le bloc « toujours » dans la liste 1 sera utilisé pour décrire une porte ET.

Dans un article précédent, nous nous sommes familiarisés avec le type de données Verilog « wire ». Ce type de données représente un fil physique dans notre conception FPGA. Au sein d'un bloc "toujours", la norme Verilog ne permet pas d'attribuer une valeur à un "fil". Au lieu de cela, nous utilisons le type de données « reg ». Le nom "reg" est quelque peu déroutant, mais notez qu'un "reg" peut ou non conduire à un élément de stockage physique dans votre conception. Le code suivant est la description Verilog de la figure 5 utilisant un bloc « always ». Notez que le type de données de sortie doit être « reg » car il tire sa valeur d'une affectation procédurale.

 module Circuit_1 ( fil d'entrée a, fil d'entrée b, sortie reg out1 ); toujours @ (a, b) début out1 =a &b; end endmodule 

Dans cet article, nous nous sommes familiarisés avec l'opérateur conditionnel Verilog. Nous avons utilisé la forme imbriquée de cet opérateur pour décrire un encodeur de priorité. Ensuite, nous avons abordé une construction de langage plus puissante, le bloc « toujours », pour décrire les circuits combinatoires. Dans les prochains articles, nous examinerons l'utilisation du bloc « always » pour implémenter des circuits séquentiels.