Décibels

Le Bel est utilisé pour représenter le gain

Dans sa forme la plus simple, le gain d'un amplificateur est un rapport entre la sortie et l'entrée. Comme tous les ratios, cette forme de gain est sans unité. Cependant, il existe une unité réelle destinée à représenter le gain, et elle s'appelle le bel .

En tant qu'unité, le bel a en fait été conçu comme un moyen pratique de représenter la perte de pouvoir dans le câblage du système téléphonique plutôt que de gain dans les amplificateurs. Le nom de l'unité est dérivé d'Alexander Graham Bell, le célèbre inventeur écossais dont le travail a joué un rôle déterminant dans le développement des systèmes téléphoniques. À l'origine, le bel représentait la quantité de perte de puissance du signal due à la résistance sur une longueur standard de câble électrique. Maintenant, il est défini en termes de logarithme commun (base 10) d'un rapport de puissance (puissance de sortie divisée par la puissance d'entrée) :

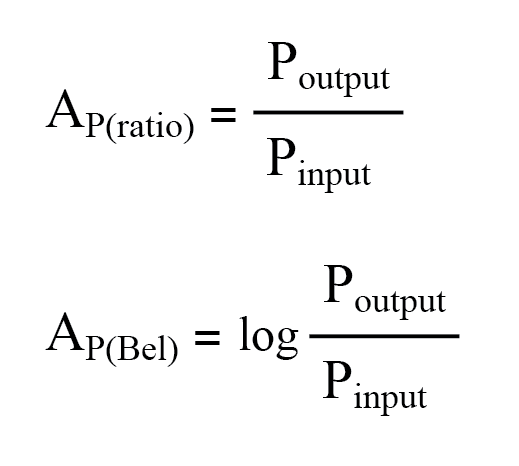
Le Bel est non linéaire

Parce que le bel est une unité logarithmique, il est non linéaire. Pour vous donner une idée de la façon dont cela fonctionne, considérez le tableau de figures suivant, comparant les pertes et les gains de puissance en bels par rapport aux rapports simples :

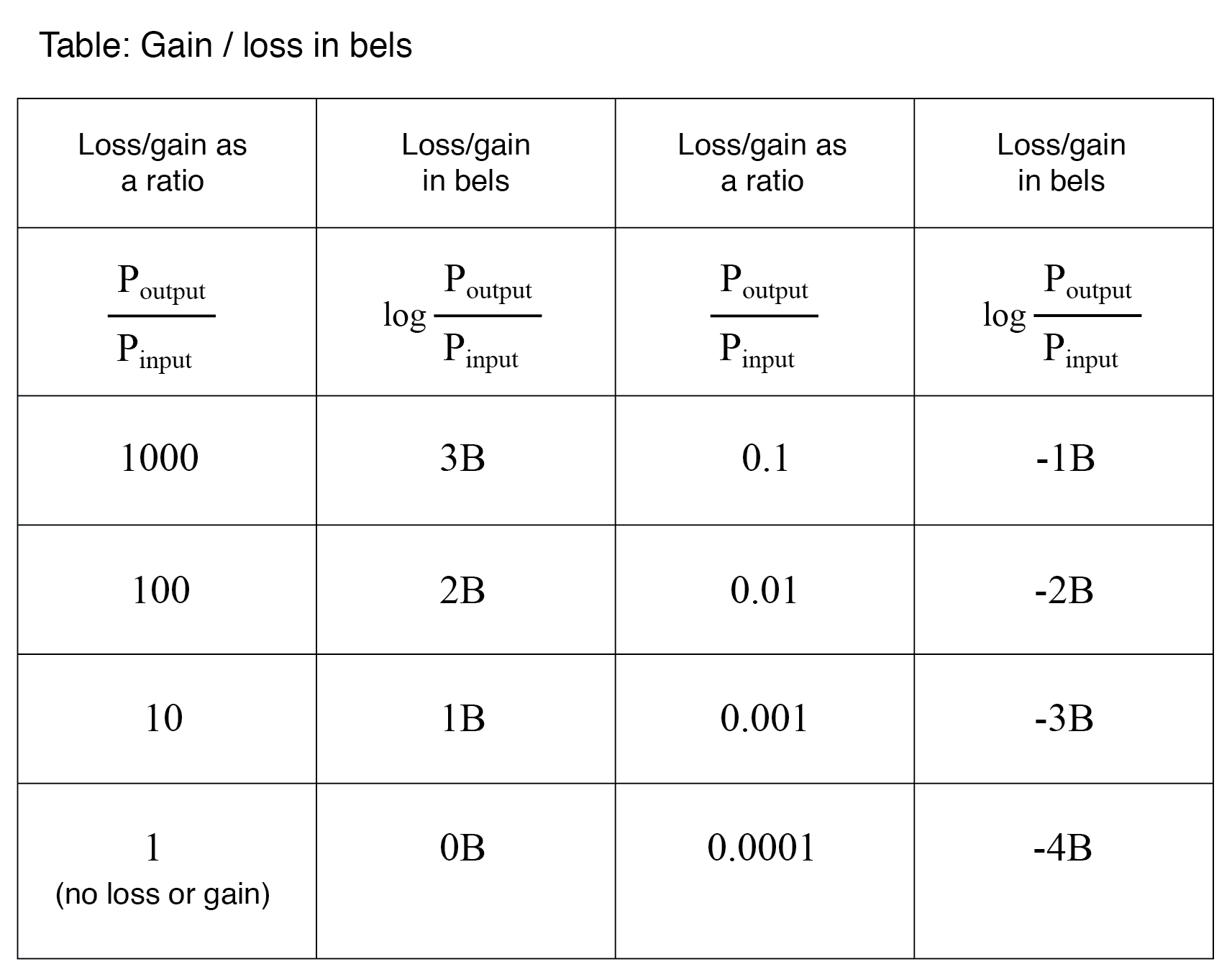
Passer du Bel au Décibel

Il a été décidé plus tard que le bel était une unité trop grande pour être utilisé directement, et il est donc devenu habituel d'appliquer le préfixe métrique deci (signifiant 1/10), ce qui en fait deci bels, ou dB. Maintenant, l'expression « dB » est si courante que beaucoup de gens ne réalisent pas qu'il s'agit d'une combinaison de « deci- » et « -bel », ou qu'il existe même une unité telle que le « bel ». Pour mettre cela en perspective, voici un autre tableau contrastant les rapports de gain/perte de puissance par rapport aux décibels :

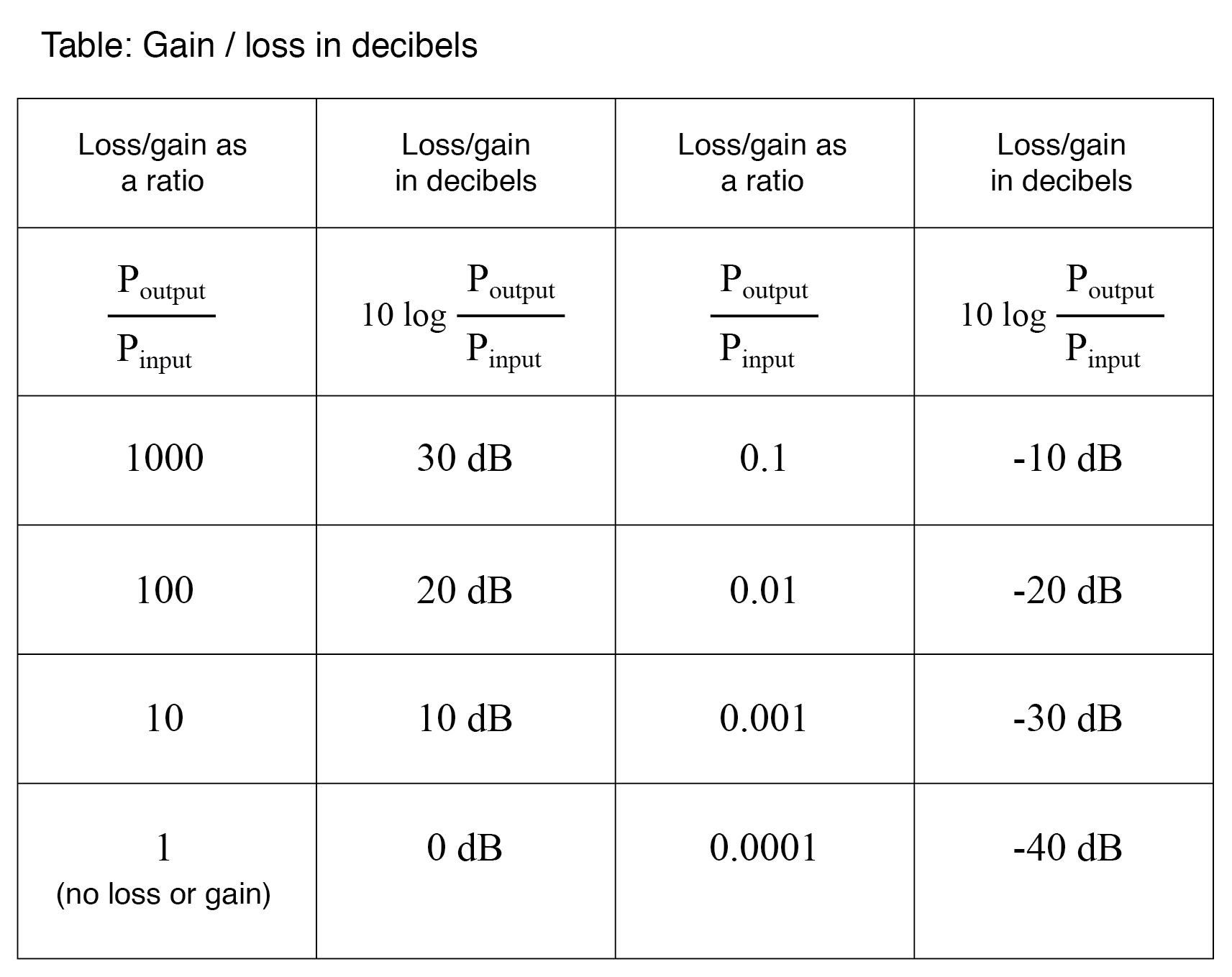
En tant qu'unité logarithmique, ce mode d'expression du gain de puissance couvre une large gamme de rapports avec une plage de chiffres minimale. Il est raisonnable de se demander :« pourquoi quelqu'un a-t-il ressenti le besoin d'inventer un logarithmique unité pour la perte de puissance du signal électrique dans un système téléphonique ? » La réponse est liée à la dynamique de l'audition humaine, dont l'intensité perceptive est de nature logarithmique.

L'audition humaine est non linéaire

L'audition humaine est fortement non linéaire :pour doubler l'intensité perçue d'un son, la puissance sonore réelle doit être multipliée par un facteur dix. Relier la perte de puissance du signal téléphonique en termes d'échelle logarithmique « bel » est parfaitement logique dans ce contexte :une perte de puissance de 1 bel se traduit par une perte sonore perçue de 50 %, ou 1/2. Un gain de puissance de 1 bel se traduit par un doublement de l'intensité perçue du son.

Autres exemples d'échelle logarithmique :échelle de Richter et pH chimique

Échelle de Richter

Une analogie presque parfaite avec l'échelle bel est l'échelle de Richter utilisée pour décrire l'intensité des tremblements de terre :un tremblement de terre de 6,0 de Richter est 10 fois plus puissant qu'un tremblement de terre de 5,0 de Richter; un séisme de 7,0 Richter 100 fois plus puissant qu'un séisme de 5,0 Richter; un séisme de Richter de 4,0 est 1/10 aussi puissant qu'un séisme de Richter de 5,0, et ainsi de suite.

PH chimique

L'échelle de mesure du pH chimique est également logarithmique, une différence de 1 sur l'échelle équivaut à une différence de dix fois la concentration en ions hydrogène d'une solution chimique. L'un des avantages de l'utilisation d'une échelle de mesure logarithmique est la vaste gamme d'expression offerte par une plage de valeurs numériques relativement petite, et c'est cet avantage qui garantit l'utilisation des nombres de Richter pour les tremblements de terre et du pH pour l'activité des ions hydrogène.

Utiliser Bel pour exprimer les gains et les pertes du système

Une autre raison de l'adoption du bel comme unité de gain est la simple expression des gains et des pertes du système. Considérons le dernier exemple de système (figure ci-dessus) où deux amplificateurs ont été connectés en tandem pour amplifier un signal. Le gain respectif de chaque amplificateur était exprimé sous forme de rapport, et le gain global du système était le produit (multiplication) de ces deux rapports :

Gain global =(3)(5) =15

Si ces chiffres représentaient la puissance gains, nous pourrions appliquer directement l'unité de bels à la tâche de représenter le gain de chaque amplificateur et du système dans son ensemble. (Figure ci-dessous)

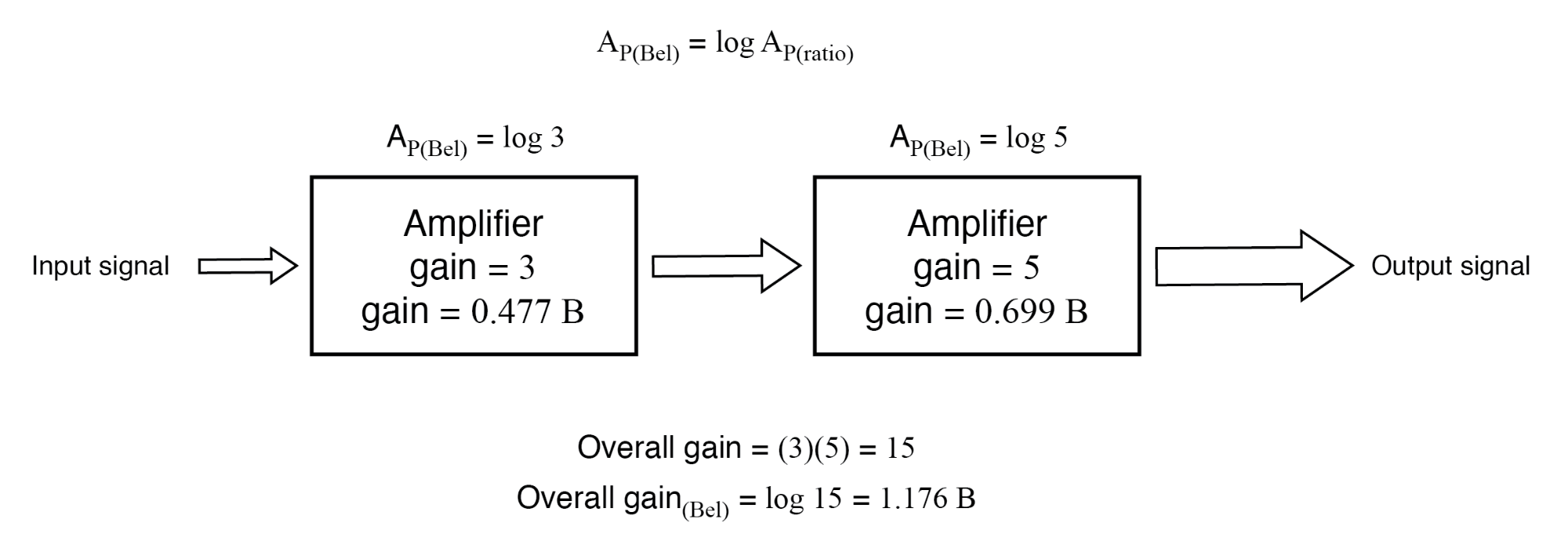
Le gain de puissance en bels est additif :0,477 B + 0,699 B =1,176 B.

Un examen attentif de ces chiffres de gain dans l'unité de « bel » conduit à une découverte :ils sont additifs. Les chiffres de gain de rapport sont multiplicatifs pour les amplificateurs étagés, mais les gains exprimés en bels add plutôt que de multiplier égal au gain global du système. Le premier amplificateur avec son gain de puissance de 0,477 B s'ajoute au gain de puissance du second amplificateur de 0,699 B pour créer un système avec un gain de puissance global de 1,176 B.

Gagne en utilisant les décibels

En recalculant pour les décibels plutôt que les bels, on constate le même phénomène. (Figure ci-dessous)

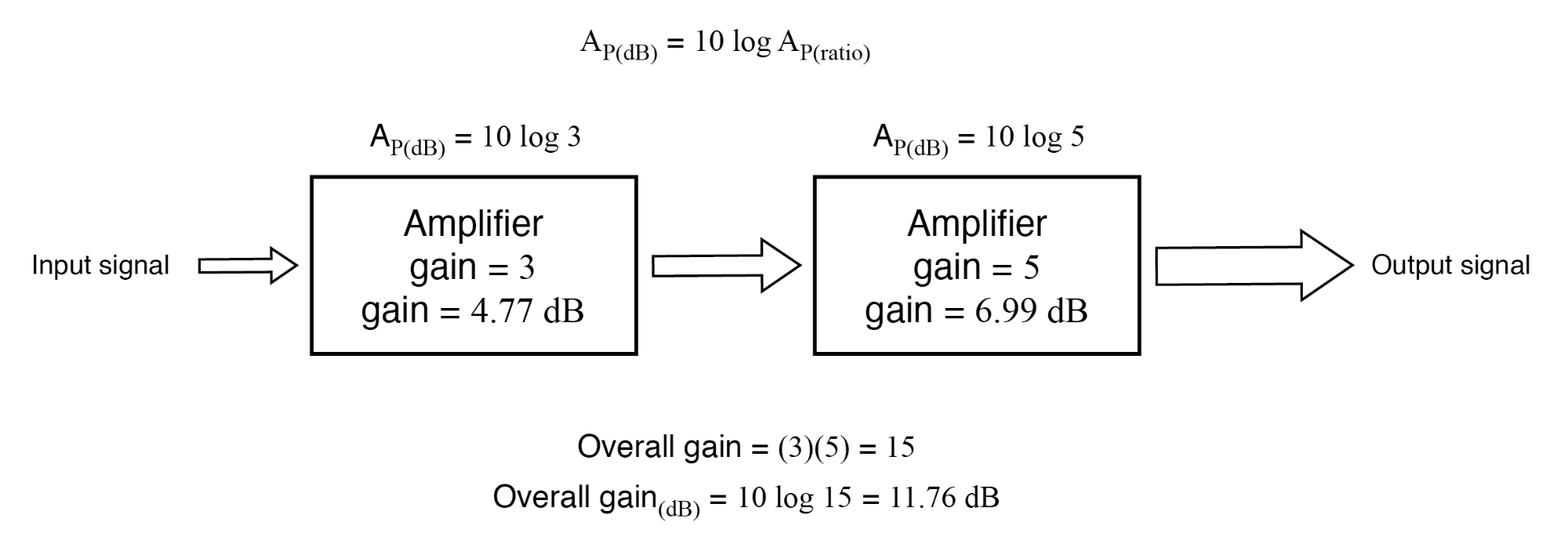
Le gain des étages d'amplification en décibels est additif :4,77 dB + 6,99 dB =11,76 dB.

Pour ceux qui connaissent déjà les propriétés arithmétiques des logarithmes, ce n'est pas une surprise. C'est une règle élémentaire de l'algèbre que l'antilogarithme de la somme des valeurs du logarithme de deux nombres est égal au produit des deux nombres originaux. En d'autres termes, si nous prenons deux nombres et déterminons le logarithme de chacun, puis additionnons ces deux chiffres du logarithme, puis déterminons l'"antilogarithme" de cette somme (élevons le nombre de base du logarithme - dans ce cas, 10 - au puissance de cette somme), le résultat sera le même que si nous avions simplement multiplié les deux nombres originaux.

Cette règle algébrique forme le cœur d'un dispositif appelé règle à calcul , un ordinateur analogique qui pourrait, entre autres, déterminer les produits et les quotients de nombres par addition (en additionnant des longueurs physiques marquées sur des échelles coulissantes en bois, en métal ou en plastique).

Étant donné un tableau de chiffres logarithmiques, la même astuce mathématique pourrait être utilisée pour effectuer des multiplications et des divisions autrement complexes en n'ayant à faire que des additions et des soustractions, respectivement. Avec l'avènement des calculatrices numériques portables à grande vitesse, cette technique de calcul élégante a pratiquement disparu de l'utilisation populaire. Cependant, il est toujours important de comprendre lorsque vous travaillez avec des échelles de mesure de nature logarithmique, telles que les échelles bel (décibel) et Richter.

Conversion des décibels et du rapport sans unité

Lors de la conversion d'un gain de puissance à partir d'unités de bels ou de décibels en un rapport sans unité, la fonction mathématique inverse des logarithmes communs est utilisée :les puissances de 10, ou l'antilog .

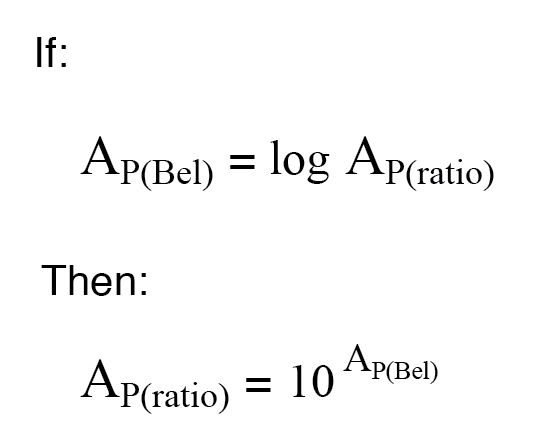
La conversion des décibels en rapports sans unité pour le gain de puissance est à peu près la même, seul un facteur de division de 10 est inclus dans le terme exposant :

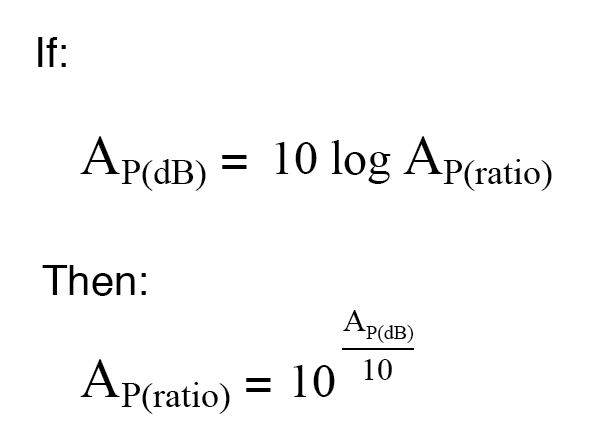
Exemple : La puissance dans un amplificateur est de 1 watt, la puissance de sortie est de 10 watts. Trouvez le gain de puissance en dB.

AP(dB) =10*log10(PO / PI) =10*log10(10 /1) =10*log10(10) =10*(1) =10 dB

Exemple : Trouvez le rapport de gain de puissance AP(ratio) =(PO / PI) pour un gain de puissance de 20 dB.

AP(dB) =20 =10*log10(APrapport ) 20/10 =log10*(APratio ) 10^(20/10) =10^(log10*(APrapport )) 10^2 =100 =AP(ratio) =(PO / PI)

Conversion du gain de puissance en gain de tension/courant

Parce que le bel est fondamentalement une unité de pouvoir gain ou perte dans un système, les gains et pertes de tension ou de courant ne se convertissent pas en bels ou en dB de la même manière. Lorsque vous utilisez des bels ou des décibels pour exprimer un gain autre que la puissance, qu'il s'agisse de tension ou de courant, nous devons effectuer le calcul en termes de gain de puissance pour cette quantité de tension ou de gain de courant.

Pour une impédance de charge constante, un gain de tension ou de courant de 2 équivaut à un gain de puissance de 4 (2 ² ); un gain de tension ou de courant de 3 équivaut à un gain de puissance de 9 (3 ² ). Si nous multiplions la tension ou le courant par un facteur donné, alors le gain de puissance engendré par cette multiplication sera le carré de ce facteur. Cela renvoie aux formes de la loi de Joule où la puissance était calculée à partir de la tension ou du courant, et de la résistance :

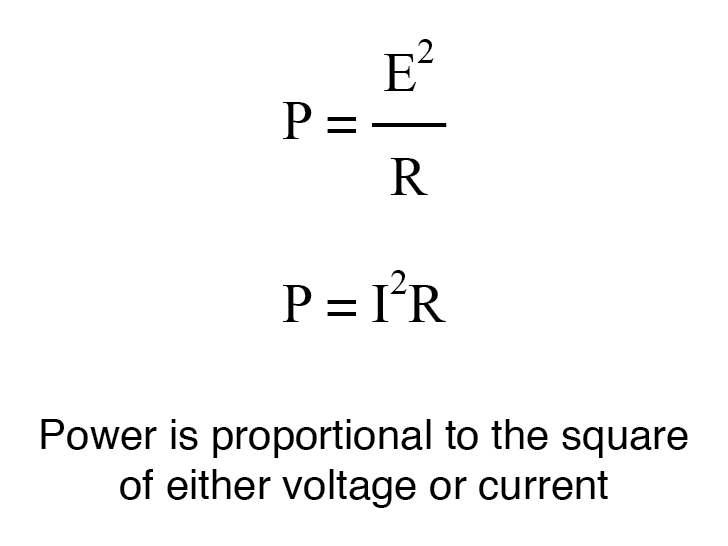
Ainsi, lors de la traduction d'un rapport de gain de tension ou de courant en un gain respectif en termes d'unité bel, nous devons inclure cet exposant dans la ou les équations :

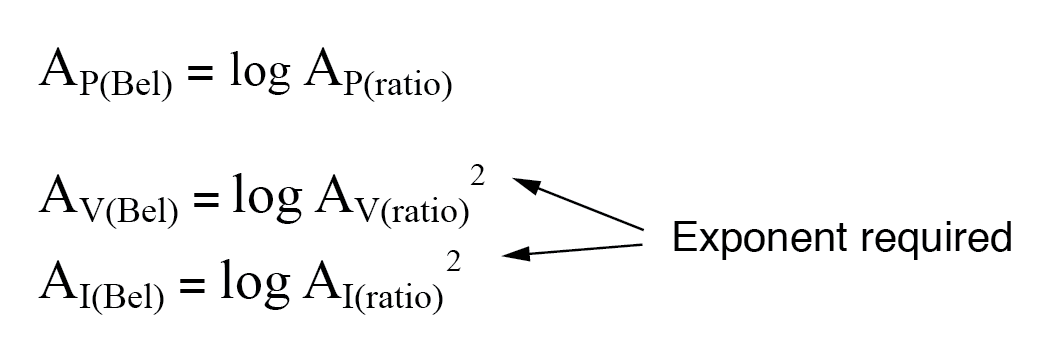
La même exigence d'exposant s'applique lors de l'expression des gains de tension ou de courant en termes de décibels :

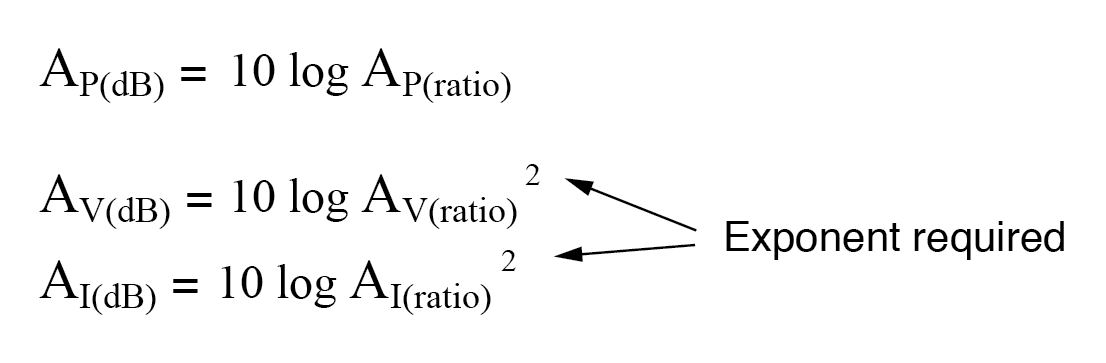
Cependant, grâce à une autre propriété intéressante des logarithmes, nous pouvons simplifier ces équations pour éliminer l'exposant en incluant le « 2 » comme facteur multiplicateur pour la fonction logarithme. Autrement dit, au lieu de prendre le logarithme du carré du gain de tension ou de courant, nous multiplions simplement le logarithme du gain de tension ou de courant par 2 et le résultat final en bels ou en décibels sera le même :

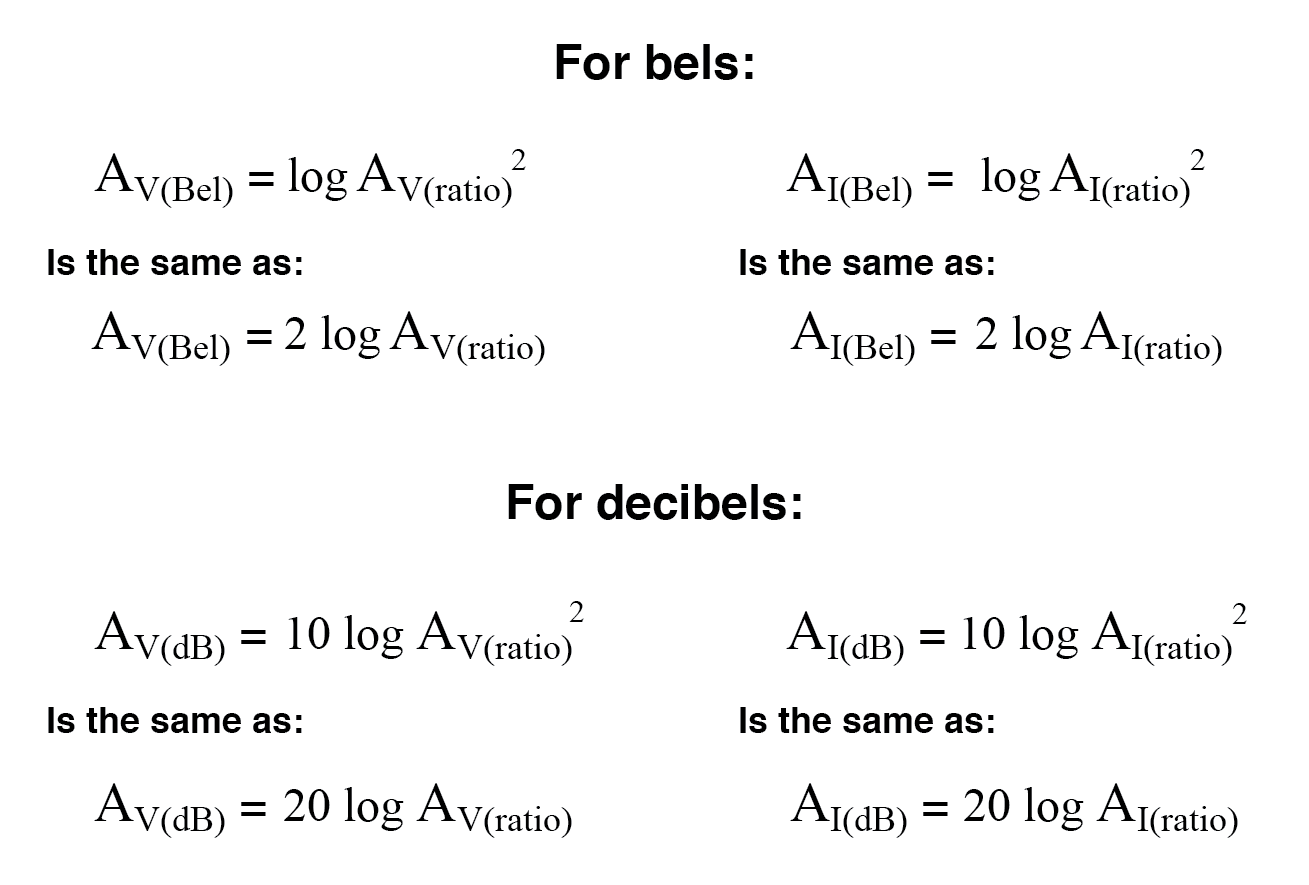
Le processus de conversion des gains de tension ou de courant des bels ou des décibels en rapports sans unité est à peu près le même que pour les gains de puissance :

Voici les équations utilisées pour convertir les gains de tension ou de courant en décibels en ratios sans unité :

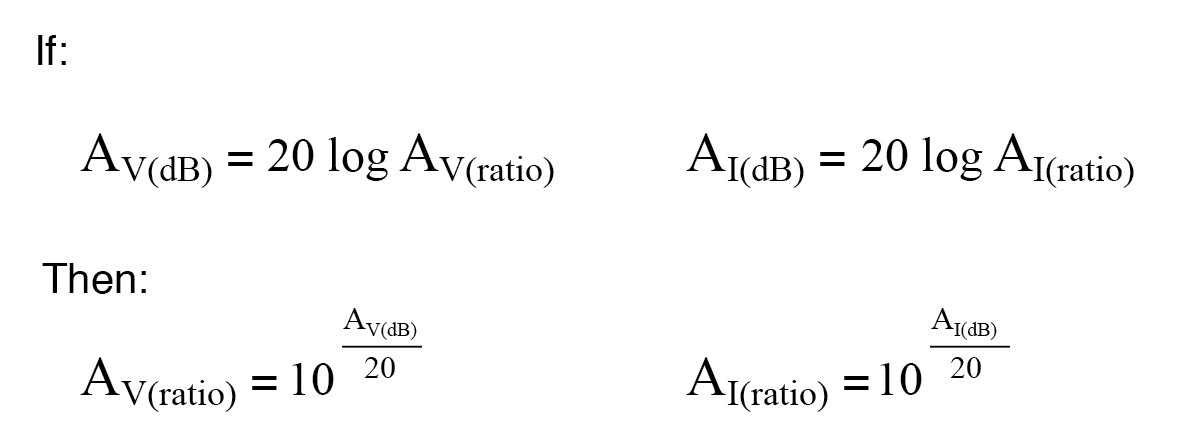
Alors que le bel est une unité naturellement mise à l'échelle pour la puissance, une autre unité logarithmique a été inventée pour exprimer directement les gains/pertes de tension ou de courant, et elle est basée sur le naturel logarithme plutôt que le commun logarithme comme le sont les bels et les décibels. Appelé le neper , son symbole unitaire est « Np; cependant, des « n » minuscules peuvent être rencontrés.

Pour le meilleur ou pour le pire, ni le néper ni son cousin atténué, le decineper , est couramment utilisé comme unité dans les applications d'ingénierie américaines. Exemple : La tension dans un amplificateur de ligne audio de 600 est de 10 mV, la tension aux bornes d'une charge de 600 est de 1 V. Trouvez le gain de puissance en dB.

A(dB) =20 log10(VO / VI) =20 log10 (1 /0,01) =20 log10 (100) =20 (2) =40 dB

Exemple : Trouvez le rapport de gain en tension AV(rapport) =(VO / VI) pour un amplificateur à gain de 20 dB ayant une impédance d'entrée et de sortie de 50 .

AV(dB) =20 log10 AV(ratio) 20 =20 log10 AV(ratio) 20/20 =log10 AP(ratio) 1020/20 =10log10 (AV(ratio)) 10 =AV(ratio) =( VO/VI)

Un examen du décibel

• Les gains et les pertes peuvent être exprimés en termes de rapport sans unité, ou dans l'unité de bels (B) ou de décibels (dB). Un décibel est littéralement un déci -bel :un dixième de bel.
• Le bel est fondamentalement une unité d'expression du pouvoir BENEFICE ou PERTE. Pour convertir un rapport de puissance en bels ou en décibels, utilisez l'une de ces équations :

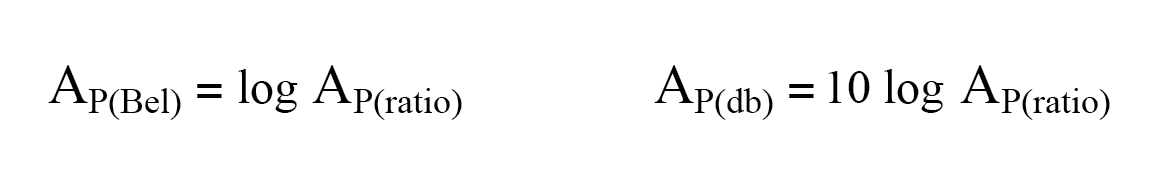
• Lors de l'utilisation de l'unité du bel ou du décibel pour exprimer une tension ou actuel rapport, il doit être exprimé en termes de puissance équivalente rapport. Concrètement, cela signifie l'utilisation de différentes équations, avec un facteur de multiplication de 2 pour la valeur du logarithme correspondant à un exposant de 2 pour le rapport de gain en tension ou en courant :

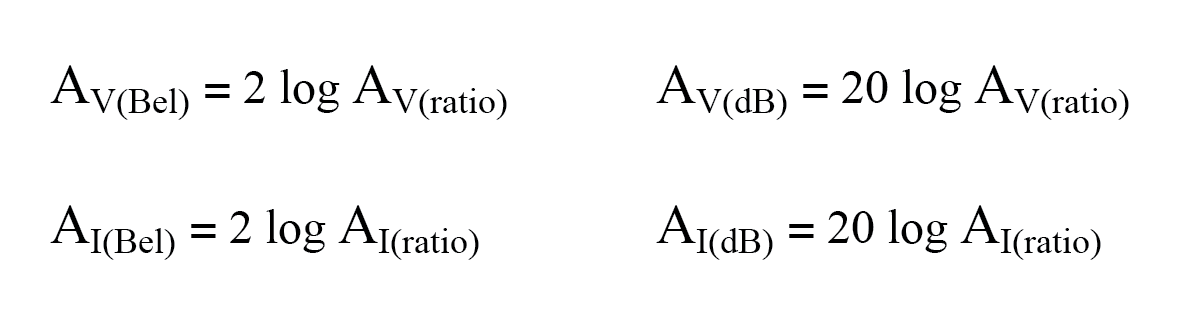
• Pour convertir un gain en décibels en un gain de rapport sans unité, utilisez l'une de ces équations :

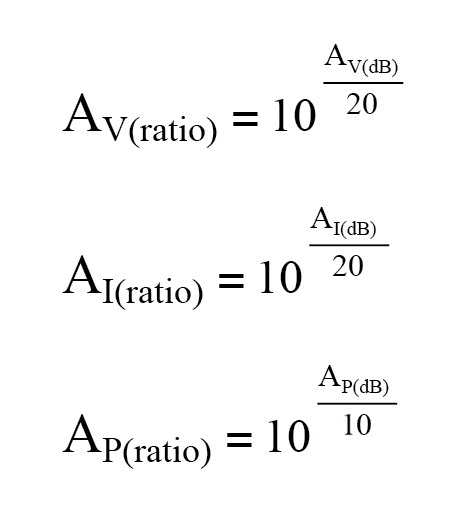
• Un gain (amplification) est exprimé sous la forme d'un chiffre positif en bel ou en décibel. Une perte (atténuation) est exprimée sous la forme d'un chiffre négatif en bel ou en décibel. Le gain unitaire (pas de gain ni de perte ; rapport =1) est exprimé en zéro bel ou zéro décibel.
• Lors du calcul du gain global d'un système d'amplification composé de plusieurs étages d'amplification, les rapports de gain individuels sont multipliés pour trouver le rapport de gain global. Les chiffres en bel ou en décibel pour chaque étage d'amplification, en revanche, sont ajoutés ensemble pour déterminer le gain global.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les mesures des décibels
• Fiche de travail sur la théorie des amplificateurs élémentaires