Chiffres et symboles

L'expression de quantités numériques est quelque chose que nous avons tendance à tenir pour acquis. C'est à la fois une bonne et une mauvaise chose dans l'étude de l'électronique.

C'est bien, dans la mesure où nous sommes habitués à l'utilisation et à la manipulation des nombres pour les nombreux calculs utilisés dans l'analyse des circuits électroniques.

D'un autre côté, le système de notation particulier qui nous a été enseigné depuis l'école primaire n'est pas le système utilisé en interne dans les appareils informatiques électroniques modernes, et l'apprentissage de tout système de notation différent nécessite un réexamen d'hypothèses profondément enracinées.

Chiffres

Tout d'abord, nous devons distinguer la différence entre les nombres et les symboles que nous utilisons pour représenter les nombres. Un nombre est une quantité mathématique, généralement corrélée en électronique à une quantité physique telle que la tension, le courant ou la résistance. Il existe de nombreux types de nombres différents. Voici quelques types, par exemple :

NOMBRE ENTIER :
1, 2, 3, 4, 5, 6, 7, 8, 9 . . .

ENTIERS :
-4, -3, -2, -1, 0, 1, 2, 3, 4 . . .

NUMÉROS IRRATIONNELS :
π (environ 3,1415927),
e (environ 2,718281828),
racine carrée de tout nombre premier

VÉRITABLES CHIFFRES :
(Toutes les valeurs numériques unidimensionnelles, négatives et positives,
y compris les nombres zéro, entiers, entiers et irrationnels)

NUMÉROS COMPLEXES :
3 - j4 , 34,5 20 ^o

Différents types de nombres trouvent des applications différentes dans le monde physique. Les nombres entiers fonctionnent bien pour compter des objets discrets, tels que le nombre de résistances dans un circuit. Les nombres entiers sont nécessaires lorsque des équivalents négatifs de nombres entiers sont requis.

Les nombres irrationnels sont des nombres qui ne peuvent pas être exactement exprimés comme le rapport de deux nombres entiers, et le rapport de la circonférence d'un cercle parfait à son diamètre (π) en est un bon exemple physique. Les quantités non entières de tension, de courant et de résistance auxquelles nous sommes habitués dans les circuits CC peuvent être exprimées sous forme de nombres réels, sous forme fractionnaire ou décimale.

Pour l'analyse des circuits alternatifs, cependant, les nombres réels ne parviennent pas à capturer la double essence de la magnitude et de l'angle de phase, et nous nous tournons donc vers l'utilisation de nombres complexes sous forme rectangulaire ou polaire.

Symboles

Si nous devons utiliser des nombres pour comprendre les processus du monde physique, faire des prédictions scientifiques ou équilibrer nos chéquiers, nous devons avoir un moyen de les désigner symboliquement.

En d'autres termes, nous pouvons savoir combien d'argent nous avons sur notre compte courant, mais pour en garder une trace, nous devons avoir un système élaboré pour symboliser cette quantité sur papier, ou sous un autre type de forme pour la tenue de registres et suivi.

Analogique et numérique

Il y a deux manières de faire cela :analogique et numérique. Avec la représentation analogique, la quantité est symbolisée de manière divisible à l'infini. Avec la représentation numérique, la quantité est symbolisée de manière discrètement conditionnée.

Représentation analogique

Vous êtes probablement déjà familiarisé avec une représentation analogique de l'argent et ne l'avez pas réalisé pour ce que c'était. Avez-vous déjà vu une affiche de collecte de fonds faite avec une image d'un thermomètre dessus, où la hauteur de la colonne rouge indiquait le montant d'argent collecté pour la cause ? Plus l'argent collecté est élevé, plus la colonne d'encre rouge sur l'affiche est haute.

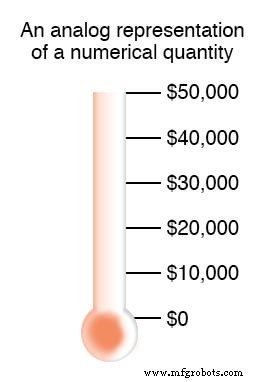
Ceci est un exemple de représentation analogique d'un nombre. Il n'y a pas de limite réelle à la façon dont la hauteur de cette colonne peut être finement divisée pour symboliser le montant d'argent sur le compte. Changer la hauteur de cette colonne est quelque chose qui peut être fait sans changer la nature essentielle de ce qu'elle est.

La longueur est une quantité physique qui peut être divisée aussi petite que vous le souhaitez, sans limite pratique. La règle à calcul est un dispositif mécanique qui utilise la même quantité physique - la longueur - pour représenter des nombres et pour aider à effectuer des opérations arithmétiques avec deux nombres ou plus à la fois. C'est aussi un appareil analogique.

Représentation numérique

En revanche, un numérique la représentation de ce même chiffre monétaire, écrite avec des symboles standard (parfois appelés chiffres), ressemble à ceci :

35 955,38 $

Contrairement à l'affiche « thermomètre » avec sa colonne rouge, ces caractères symboliques ci-dessus ne peuvent pas être finement divisés :cette combinaison particulière de chiffres représente une quantité et une seule quantité.

Si plus d'argent est ajouté au compte (+ 40,12 $), différents symboles doivent être utilisés pour représenter le nouveau solde (35 995,50 $), ou au moins les mêmes symboles disposés selon des motifs différents. Ceci est un exemple de représentation numérique.

Le pendant de la règle à calcul (analogique) est aussi un appareil numérique :le boulier, avec des billes qui se déplacent d'avant en arrière sur des tiges pour symboliser des quantités numériques :

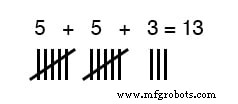
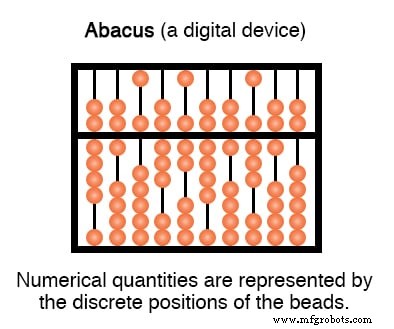
Contraste entre la représentation analogique et numérique

Comparons ces deux méthodes de représentation numérique :

ANALOGIQUE NUMÉRIQUE
------------------------------------------------------------ --------------------
Intuitivement compris ----------- Nécessite une formation pour interpréter
Infiniment divisible --- ----------- Discret
Susceptible aux erreurs de précision ------ Précision absolue

L'interprétation des symboles numériques est quelque chose que nous avons tendance à tenir pour acquis car elle nous a été enseignée pendant de nombreuses années. Cependant, si vous essayiez de communiquer une quantité de quelque chose à une personne ignorant les chiffres décimaux, cette personne pourrait toujours comprendre le simple graphique du thermomètre !

Les comparaisons infiniment divisibles vs discrètes et de précision sont vraiment les revers d'une même médaille. Le fait que la représentation numérique soit composée de symboles individuels et discrets (chiffres décimaux et boulier) signifie nécessairement qu'elle sera capable de symboliser des quantités par étapes précises.

D'un autre côté, une représentation analogique (comme la longueur d'une règle à calcul) n'est pas composée d'étapes individuelles, mais plutôt d'une gamme continue de mouvements. La capacité d'une règle à calcul à caractériser une quantité numérique à une résolution infinie est un compromis pour l'imprécision.

Si une règle à calcul est déplacée, une erreur sera introduite dans la représentation du nombre qui y a été « entré ». Cependant, un boulier doit être cogné beaucoup plus fort avant que ses billes ne soient complètement délogées de leur place (suffisant pour représenter un nombre différent).

Ne vous méprenez pas sur cette différence de précision en pensant que la représentation numérique est nécessairement plus précise que l'analogique. Ce n'est pas parce qu'une horloge est numérique qu'elle lira toujours l'heure avec plus de précision qu'une horloge analogique, cela signifie simplement que l'interprétation de son affichage est moins ambigu.

La divisibilité de la représentation analogique par rapport à la représentation numérique peut être davantage éclairée en parlant de la représentation des nombres irrationnels. Les nombres tels que π sont appelés irrationnels, car ils ne peuvent pas être exactement exprimés sous forme de fraction d'entiers ou de nombres entiers.

Bien que vous ayez peut-être appris par le passé que la fraction 22/7 peut être utilisée pour π dans les calculs, ce n'est qu'une approximation. Le nombre réel « pi » ne peut pas être exprimé exactement par un nombre fini ou limité de décimales. Les chiffres de π s'éternisent :

3.1415926535897932384 . . . . .

Il est possible, au moins théoriquement, de définir une règle à calcul (ou même une colonne de thermomètre) de manière à représenter parfaitement le nombre π, car les symboles analogiques n'ont pas de limite minimale au degré d'augmentation ou de diminution.

Si ma règle à calcul affiche un chiffre de 3,141593 au lieu de 3,141592654, je peux déplacer la diapositive un peu plus (ou moins) pour la rapprocher encore. Cependant, avec une représentation numérique, comme avec un boulier, j'aurais besoin de tiges supplémentaires (espaces réservés ou chiffres) pour représenter π à des degrés de précision supplémentaires.

Un boulier avec 10 tiges ne peut tout simplement pas représenter plus de 10 chiffres du nombre π, quelle que soit la façon dont je place les perles. Pour représenter parfaitement π, un boulier devrait avoir un nombre infini de billes et de tiges ! Le compromis, bien sûr, est la limitation pratique de l'ajustement et de la lecture des symboles analogiques.

En pratique, on ne peut pas lire l'échelle d'une règle à calcul au 10e chiffre de précision, car les marques sur l'échelle sont trop grossières et la vision humaine est trop limitée. Un abaque, en revanche, peut être installé et lu sans aucune erreur d'interprétation.

De plus, les symboles analogiques nécessitent une sorte de norme par laquelle ils peuvent être comparés pour une interprétation précise. Les règles à calcul ont des marques imprimées le long des glissières pour traduire la longueur en quantités standard.

Même le graphique du thermomètre a des chiffres écrits le long de sa hauteur pour montrer combien d'argent (en dollars) la colonne rouge représente pour une hauteur donnée. Imaginez si nous essayions tous de nous communiquer des nombres simples en espaçant nos mains à des distances variables.

Le numéro 1 peut être signifié en tenant nos mains à 1 pouce l'une de l'autre, le numéro 2 à 2 pouces, et ainsi de suite. Si quelqu'un tenait ses mains à 17 pouces l'un de l'autre pour représenter le nombre 17, est-ce que tout le monde autour d'eux serait capable d'interpréter immédiatement et avec précision cette distance comme 17 ? Probablement pas.

Certains devineraient court (15 ou 16) et certains devineraient long (18 ou 19). Bien sûr, les pêcheurs qui se vantent de leurs prises ne craignent pas les surestimations en quantité !

C'est peut-être pour cette raison que les gens ont généralement opté pour des symboles numériques pour représenter les nombres, en particulier les nombres entiers et les nombres entiers, qui trouvent le plus d'applications dans la vie de tous les jours.

En utilisant les doigts de nos mains, nous avons un moyen tout prêt de symboliser des nombres entiers de 0 à 10. Nous pouvons faire des marques de hachage sur du papier, du bois ou de la pierre pour représenter les mêmes quantités assez facilement :

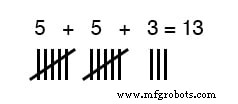
Pour les grands nombres, cependant, le système de numération "dièse" est trop inefficace.