Algorithme efficace d'optimisation des variables orthogonales pour les systèmes de communication

Cet article traite d'un algorithme pour trouver le point ajusté optimal dans un espace à deux dimensions avec des vecteurs d'entrée orthogonaux. L'algorithme résout les équations des cercles sécants en fonction des points de données mesurés.

Plusieurs mesures clés de performance du système sont déterminées par des paramètres d'entrée orthogonaux correspondant à l'amplitude et à la phase ; deux exemples sont la traversée de porteuse du modulateur en quadrature et la suppression de bande latérale. Ces paramètres sont améliorés en optimisant l'équilibre de décalage CC et l'équilibre d'amplitude et de phase entre les entrées de bande de base en quadrature du modulateur.

Parce que trouver l'ajustement optimal de ces paramètres n'est pas une tâche triviale étant donné l'espace à deux dimensions, dans cet article, je vais discuter d'un algorithme Python pour trouver le point ajusté optimal dans un espace à deux dimensions avec des vecteurs d'entrée orthogonaux. L'algorithme résout les équations des cercles sécants sur la base des points de données mesurés et trouve le point optimal en seulement quatre itérations. Pour illustrer la technique, j'ai utilisé le convertisseur numérique-analogique (DAC) intégré Texas Instruments (TI) AFE7070 ainsi que le paramètre de traversée de porteuse du modulateur en quadrature.

Optimisation des émissions parasites

Les systèmes de communication s'efforcent de minimiser les émissions parasites. Certaines de ces émissions parasites proviennent d'une désadaptation orthogonale du signal d'entrée. Par exemple, la non-concordance de décalage CC et le déséquilibre amplitude/phase affecteront respectivement les paramètres de traversée de porteuse et de suppression de bande latérale dans les modulateurs analogiques en quadrature. L'ajustement des variables d'entrée à un point de consigne optimal minimise les sorties parasites.

La figure 1 représente le paramètre mesuré comme l'amplitude (r) du vecteur du point optimisé, [x0,y0], au point réel sur un plan à deux dimensions. La valeur du paramètre est délimitée par [0,1], un cercle unitaire. Un 0 représente une annulation complète ou aucun signal et un 1 représente aucune annulation ou un signal complet. Dans les échelles de décibels, la fonction est liée par [-inf,0]. Le cercle de rayon r représente tous les points x,y possibles qui atteignent la même magnitude.

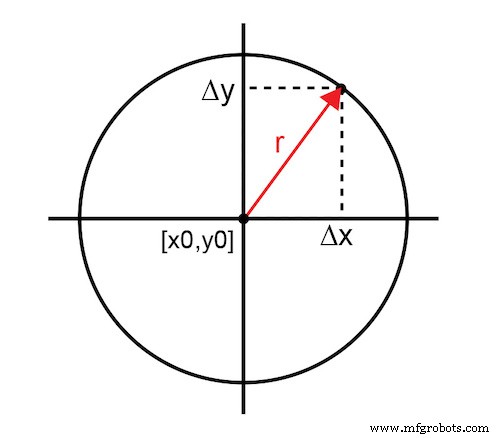
Figure 1. Vecteur du point optimisé au point réel

L'équation 1 représente la fonction dans sa forme la plus simple :

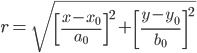(1)

Les constantes [a0,b0] représentent des facteurs de normalisation dépendants du système pour maintenir le résultat maximum inférieur à 1. Techniquement, l'équation 1 décrit une ellipse, car les facteurs d'échelle pour chaque variable indépendante n'ont pas besoin d'être les mêmes. Pour simplifier cette analyse, a0 est égal à b0 de sorte que les courbes sont vraiment des cercles.

Le but est de trouver le point optimal [x0,y0] qui minimise le paramètre de mesure (r) le plus rapidement possible. Il est difficile de trouver ce point efficacement avec des paramètres d'entrée statistiquement variables. L'approche traditionnelle de chasse et de picorage utilise des essais successifs pour affiner jusqu'au point optimal. Bien que cela donne la solution souhaitée, cela prend trop d'itérations lorsque le temps de convergence est critique, ce qui nécessite une nouvelle méthode.

Cercles qui se croisent

Idéalement, exactement trois itérations de mesure utilisant des cercles sécants déterminent le point optimal. Le premier résultat mesuré à un point d'entrée arbitraire [x1,y1] définit des possibilités infinies pour le point optimal représenté par le cercle A de rayon r1. L'ajout d'un deuxième point de données produit un autre ensemble de données infini représenté par le cercle B ; cependant, les intersections des deux cercles rétrécissent la solution à deux points. Un troisième point de données et le cercle correspondant C fournissent une troisième courbe où il n'y a qu'un seul point d'intersection mutuelle. Ce point d'intersection est le point optimal. La figure 2 montre la progression des cercles sécants qui culminent dans le point optimal définitif.

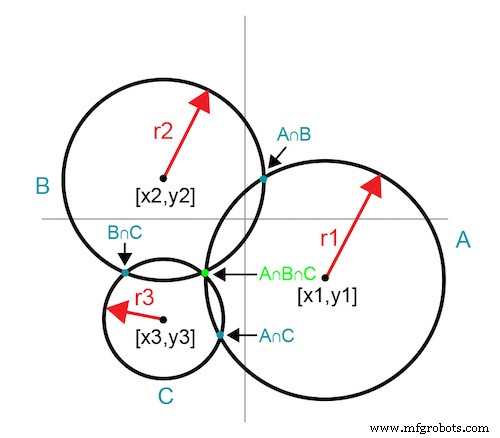
Figure 2. Les cercles qui se croisent révèlent un point d'intersection commun

Cette technique révèle le point optimal en exactement trois itérations. Une quatrième itération mesure le point optimal pour confirmer et documenter le résultat.

La figure 3 illustre une technique pour éliminer une itération en utilisant des informations de frontière connues empiriquement dans le plan x-y. Sélectionnez le point initial à l'un des points limites de sorte que la première courbe (A) soit un arc de 90 degrés. Sélectionnez le deuxième point sur le premier arc en vous déplaçant dans la direction x ou y.

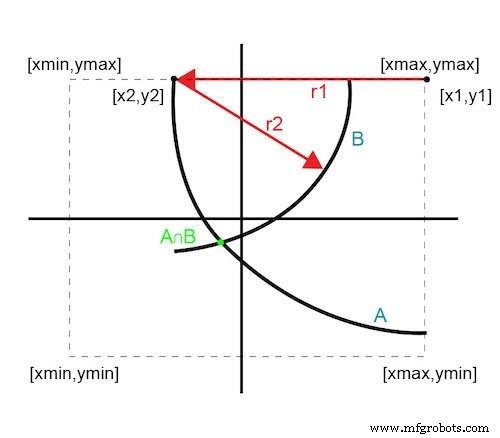
Figure 3. Solution à deux itérations

Étant donné que le deuxième point se trouve toujours sur le bord limite, sa courbe est un arc inférieur à 180 degrés. L'intersection de ces deux courbes fournit un seul point optimal. Cette approche révèle le point optimal en seulement deux itérations et le confirme avec trois.

Approximation de cercles successifs

La solution optimale dépend de la précision de l'équation mathématique. Dans une situation de mesure réelle, plusieurs hypothèses ou erreurs auront un impact sur les résultats. Les signaux mesurés sont très faibles; les tolérances de bruit et de mesure introduisent des erreurs. L'utilisation de cercles parfaits au lieu d'ellipses introduit une certaine incertitude. Les hypothèses de facteur d'échelle nécessaires pour résoudre plusieurs équations introduisent également une incertitude. Ces erreurs et hypothèses se traduisent par un flou dans les courbes.

La figure 4 illustre comment les courbes floues ne garantissent pas un point d'intersection exact ; au lieu de cela, ils définissent une zone de convergence.

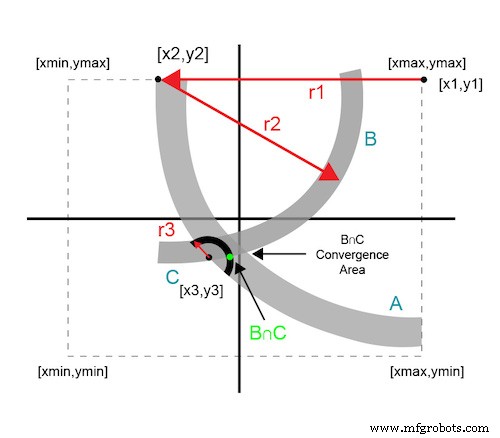
Figure 4. Approximation d'intersection de cercles successifs

Chaque point de données supplémentaire utilise les données de l'itération précédente. Les cercles successifs convergent vers une zone de solution qui se situe dans le seuil minimum du système.

Exemple de mesure

L'exemple utilise le DAC AFE7070 et optimise le paramètre de traversée de porteuse. L'AFE7070 est une plate-forme pratique, puisque le DAC et le modulateur sont intégrés. Le déséquilibre de décalage CC sur les entrées en quadrature du modulateur détermine les performances de traversée de la porteuse. L'AFE7070 dispose d'une fonction de réglage numérique interne pour contrôler minutieusement la balance de décalage CC. Il ne faut pas grand-chose; la résolution est à l'échelle du microvolt.

Les paramètres x,y de l'exemple sont des valeurs de pas numériques entières qui contrôlent le niveau CC sur les entrées en quadrature. L'échantillonnage statistique précédent de l'appareil a fourni les limites x,y des variables d'entrée ainsi que les tables de pas utilisées dans les calculs. Les tableaux de pas fournissent une « conversion » d'une traversée de porteuse mesurée en décibels milliwatts en un facteur delta-x (ou delta-y).

Une valeur mesurée élevée (ou en d'autres termes, mauvaise) signifie que le réglage est loin et nécessite un delta plus important pour atteindre le point optimal. A l'inverse, une valeur faible signifie que la consigne est proche et nécessite une petite correction. Ce peu de « devoirs » est nécessaire pour s'assurer que les points de conjecture initiaux ne sont pas trop éloignés et pour réduire le temps d'itération au strict minimum.

La figure 5 montre l'algorithme Python qui trouve les variables d'entrée optimales en quatre itérations ou moins.

Figure 5. Algorithme d'optimisation Python

Les fonctions « Get_r » et « GetCFi » sont des mesures spécifiques à l'appareil. J'ai omis le code par souci de concision, car il n'a pas d'importance pour la démonstration de l'algorithme d'optimisation. Dans vos applications, ces fonctions sont pertinentes pour la programmation et la mesure du paramètre de l'appareil dans votre système.

Conclusion

Pour le DAC AFE7070, dans la plupart des cas, l'algorithme optimise la traversée de la porteuse en trois itérations et en moins de 1,7 s, principalement en fonction du temps de stabilisation et de balayage de l'analyseur de spectre. Les méthodes des étapes précédentes prenaient près de 20 itérations et plus de 20 s. Cet algorithme représente une amélioration de la vitesse de plus de 10 fois par rapport à l'approche traditionnelle. D'autres paramètres du système de communication dépendant de variables d'entrée orthogonales de gain et de phase peuvent également utiliser cet algorithme pour se concentrer efficacement sur une solution optimale.

Les articles sur l'industrie sont une forme de contenu qui permet aux partenaires de l'industrie de partager des actualités, des messages et des technologies utiles avec les lecteurs d'All About Circuits d'une manière qui ne convient pas au contenu éditorial. Tous les articles de l'industrie sont soumis à des directives éditoriales strictes dans le but d'offrir aux lecteurs des nouvelles utiles, une expertise technique ou des histoires. Les points de vue et opinions exprimés dans les articles de l'industrie sont ceux du partenaire et pas nécessairement ceux d'All About Circuits ou de ses rédacteurs.